Récupération des caractéristiques noms du rapport de variance expliqué dans PCA avec sklearn
j'essaie de récupérer d'un PCA fait avec scikit-learn, qui caractéristiques sont sélectionnées comme pertinentes .
un exemple classique avec L'ensemble de données IRIS.
import pandas as pd
import pylab as pl
from sklearn import datasets
from sklearn.decomposition import PCA
# load dataset
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
# normalize data
df_norm = (df - df.mean()) / df.std()
# PCA
pca = PCA(n_components=2)
pca.fit_transform(df_norm.values)
print pca.explained_variance_ratio_
retourne
In [42]: pca.explained_variance_ratio_
Out[42]: array([ 0.72770452, 0.23030523])
Comment puis-je récupérer les deux caractéristiques qui permettent ces deux différences expliquées entre les données ? Dit diféremment, Comment puis-je obtenir l'index de ce caractéristiques dans iris.feature_names ?
In [47]: print iris.feature_names
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Merci d'avance pour votre aide.
4 réponses
cette information est incluse dans l'attribut pca : components_ . Comme décrit dans la documentation , pca.components_ sorties un tableau de [n_components, n_features] , donc pour obtenir comment les composants sont linéairement liés avec les différentes fonctionnalités que vous avez à:
Note : chaque coefficient représente la corrélation entre une paire particulière de composant et de caractéristique
import pandas as pd
import pylab as pl
from sklearn import datasets
from sklearn.decomposition import PCA
# load dataset
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
# normalize data
from sklearn import preprocessing
data_scaled = pd.DataFrame(preprocessing.scale(df),columns = df.columns)
# PCA
pca = PCA(n_components=2)
pca.fit_transform(data_scaled)
# Dump components relations with features:
print pd.DataFrame(pca.components_,columns=data_scaled.columns,index = ['PC-1','PC-2'])
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
PC-1 0.522372 -0.263355 0.581254 0.565611
PC-2 -0.372318 -0.925556 -0.021095 -0.065416
IMPORTANT: comme commentaire latéral, notez que le panneau de L'APC n'affecte pas son interprétation puisque le panneau n'affecte pas la variance contenue dans chaque composante. Seuls les signes relatifs des caractéristiques formant la dimension PCA sont importants. En fait, si vous exécutez le code PCA à nouveau, vous pourriez obtenir les dimensions PCA avec les signes inversés. Pour une intuition à ce sujet, pensez à un vecteur et à son négatif dans l'espace 3-D - les deux représentent essentiellement la même direction dans espace. Cochez ce message pour de plus amples informations.
modifier: comme d'autres ont commenté, vous pouvez obtenir les mêmes valeurs de .components_ attribut.
chaque composante principale est une combinaison linéaire des variables originales:
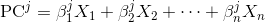
où X_i s sont les variables originales, et Beta_i s sont les poids correspondants ou soi-disant coefficients.
pour obtenir les poids, vous pouvez simplement passer la matrice d'identité à la méthode transform :
>>> i = np.identity(df.shape[1]) # identity matrix
>>> i
array([[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]])
>>> coef = pca.transform(i)
>>> coef
array([[ 0.5224, -0.3723],
[-0.2634, -0.9256],
[ 0.5813, -0.0211],
[ 0.5656, -0.0654]])
chaque colonne de la matrice coef ci-dessus indique les poids de la combinaison linéaire qui obtient l'élément principal correspondant:
>>> pd.DataFrame(coef, columns=['PC-1', 'PC-2'], index=df.columns)
PC-1 PC-2
sepal length (cm) 0.522 -0.372
sepal width (cm) -0.263 -0.926
petal length (cm) 0.581 -0.021
petal width (cm) 0.566 -0.065
[4 rows x 2 columns]
par exemple, ci-dessus montre que le deuxième composant principal ( PC-2 ) est principalement aligné avec sepal width , qui a le poids le plus élevé de 0.926 en valeur absolue;
puisque les données ont été normalisées, vous pouvez confirmer que les composantes principales ont une variance 1.0 qui est équivalente à chaque vecteur de coefficient ayant la norme 1.0 :
>>> np.linalg.norm(coef,axis=0)
array([ 1., 1.])
on peut également confirmer que les composantes principales peuvent être calculées comme le produit dot des coefficients ci-dessus et des variables originales:
>>> np.allclose(df_norm.values.dot(coef), pca.fit_transform(df_norm.values))
True
notez que nous devons utiliser numpy.allclose au lieu de "regular equality operator", à cause d'une erreur de précision en virgule flottante.
la façon dont cette question est formulée me rappelle une mauvaise compréhension de L'analyse des composantes de principe lorsque j'ai d'abord essayé de la comprendre. J'aimerais le parcourir ici dans l'espoir que les autres ne passeront pas autant de temps sur la route que je l'ai fait avant que le penny ne tombe.
la notion de" récupération " des noms de caractéristiques suggère que L'APC identifie les caractéristiques qui sont les plus importantes dans un ensemble de données. Ce n'est pas strictement vrai.
l'APC, ce que je comprends, identifie les fonctions avec la plus grande variance dans un jeu de données, et peut ensuite utiliser cette qualité de la base de données à créer un petit jeu de données avec un minimum de perte de pouvoir descriptif. Les avantages d'un ensemble de données plus petit est qu'il nécessite moins de puissance de traitement et devrait avoir moins de bruit dans les données. Mais les caractéristiques de la plus grande variance ne sont pas les "meilleures" ou les "plus importantes" caractéristiques d'un ensemble de données, dans la mesure où de tels concepts peuvent être considérés comme existant du tout.
pour introduire cette théorie dans les détails pratiques du code échantillon de @Rafa ci-dessus:
# load dataset
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
# normalize data
from sklearn import preprocessing
data_scaled = pd.DataFrame(preprocessing.scale(df),columns = df.columns)
# PCA
pca = PCA(n_components=2)
pca.fit_transform(data_scaled)
considérer ce qui suit:
post_pca_array = pca.fit_transform(data_scaled)
print data_scaled.shape
(150, 4)
print post_pca_array.shape
(150, 2)
dans ce cas, post_pca_array a les mêmes 150 lignes de données que data_scaled , mais data_scaled quatre colonnes ont été réduites de quatre à deux.
le point critique ici est que les deux colonnes – ou composantes, pour être terminologiquement cohérentes-de post_pca_array ne sont pas les deux" meilleures "colonnes de data_scaled . Il s'agit de deux nouvelles colonnes, déterminées par l'algorithme derrière le module sklearn.decomposition ’s PCA . La deuxième colonne, PC-2 dans l'exemple de @Rafa, est informée par sepal_width plus que toute autre colonne, mais les valeurs de PC-2 et data_scaled['sepal_width'] ne sont pas les mêmes.
en tant que tel, alors qu'il est intéressant de savoir combien chaque colonne dans les données originales ont contribué aux composants d'un post-PCA ensemble de données, la notion de "récupération" des noms de colonne est un peu trompeuse, et certainement m'a induit en erreur pendant une longue période. La seule situation où il y aurait une correspondance entre les colonnes post-APC et les colonnes originales serait si le nombre de composantes principales était fixé au même nombre que les colonnes dans les colonnes originales. Toutefois, il ne servirait à rien d'utiliser le même nombre de colonnes parce que les données n'auraient pas changé. Tu ne serais allé là-bas que pour revenir, pour ainsi dire.
étant donné votre estimateur ajusté pca , les composantes se trouvent dans pca.components_ , qui représentent les directions de la variance la plus élevée dans l'ensemble de données.