Analyse en composantes principales (PCA) en Python

J'ai posté ma réponse même si une autre réponse a déjà été acceptée; la réponse acceptée repose sur une fonction obsolète ; de plus, Cette fonction obsolète est basée sur décomposition de la valeur singulière (SVD), qui (bien que parfaitement valide) est la plus gourmande en mémoire et en Processeur des deux techniques générales de calcul de PCA. Ceci est particulièrement pertinent ici en raison de la taille du tableau de données dans L'OP. en utilisant PCA basé sur la covariance, le tableau utilisé dans le flux de calcul est juste 144 x 144 , plutôt que 26424 x 144 (Les dimensions du tableau de données d'origine).

Voici une implémentation de travail simple de PCA en utilisant le linalg module de SciPy . Comme cette implémentation calcule d'abord la matrice de covariance, puis effectue tous les calculs suivants sur ce tableau, elle utilise beaucoup moins de mémoire que le PCA basé sur SVD.

(le module linalg dans NumPy peut également être utilisé sans changement dans le code ci-dessous en dehors de l'instruction import, qui serait de numpy import linalg as LA.)

Les deux étapes clés de cette mise en œuvre de L'APC sont:

• Le Calcul de la matrice de covariance; et

• La Prise de la eivenvectors & les valeurs propres de cette cov de la matrice

Dans la fonction ci-dessous, le paramètre dims_rescaled_data fait référence au nombre de dimensions souhaité dans la matrice de donnéesredimensionnée ; ce paramètre a une valeur par défaut de seulement deux dimensions, mais le code ci-dessous n'est pas limité à deux, mais il peut être n'importe quelle valeur inférieure au numéro de colonne du tableau de données d'origine.

def PCA(data, dims_rescaled_data=2):
    """
    returns: data transformed in 2 dims/columns + regenerated original data
    pass in: data as 2D NumPy array
    """
    import numpy as NP
    from scipy import linalg as LA
    m, n = data.shape
    # mean center the data
    data -= data.mean(axis=0)
    # calculate the covariance matrix
    R = NP.cov(data, rowvar=False)
    # calculate eigenvectors & eigenvalues of the covariance matrix
    # use 'eigh' rather than 'eig' since R is symmetric, 
    # the performance gain is substantial
    evals, evecs = LA.eigh(R)
    # sort eigenvalue in decreasing order
    idx = NP.argsort(evals)[::-1]
    evecs = evecs[:,idx]
    # sort eigenvectors according to same index
    evals = evals[idx]
    # select the first n eigenvectors (n is desired dimension
    # of rescaled data array, or dims_rescaled_data)
    evecs = evecs[:, :dims_rescaled_data]
    # carry out the transformation on the data using eigenvectors
    # and return the re-scaled data, eigenvalues, and eigenvectors
    return NP.dot(evecs.T, data.T).T, evals, evecs

def test_PCA(data, dims_rescaled_data=2):
    '''
    test by attempting to recover original data array from
    the eigenvectors of its covariance matrix & comparing that
    'recovered' array with the original data
    '''
    _ , _ , eigenvectors = PCA(data, dim_rescaled_data=2)
    data_recovered = NP.dot(eigenvectors, m).T
    data_recovered += data_recovered.mean(axis=0)
    assert NP.allclose(data, data_recovered)


def plot_pca(data):
    from matplotlib import pyplot as MPL
    clr1 =  '#2026B2'
    fig = MPL.figure()
    ax1 = fig.add_subplot(111)
    data_resc, data_orig = PCA(data)
    ax1.plot(data_resc[:, 0], data_resc[:, 1], '.', mfc=clr1, mec=clr1)
    MPL.show()

>>> # iris, probably the most widely used reference data set in ML
>>> df = "~/iris.csv"
>>> data = NP.loadtxt(df, delimiter=',')
>>> # remove class labels
>>> data = data[:,:-1]
>>> plot_pca(data)

Le graphique ci-dessous est une représentation visuelle de cette fonction PCA sur les données iris. Comme vous pouvez le voir, une transformation 2D sépare proprement la classe I de la classe II et de la classe III (mais pas la classe II de la classe III, qui nécessite en fait une autre dimension).

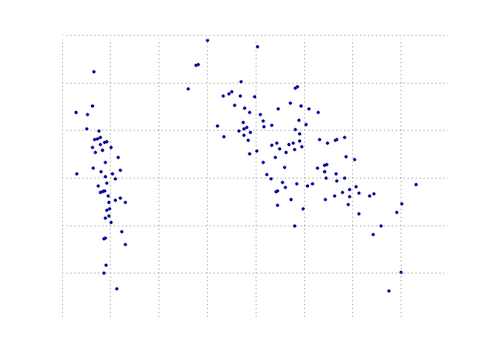
Un autre PCA Python utilisant numpy. La même idée que @ doug mais celle-là n'a pas couru.

from numpy import array, dot, mean, std, empty, argsort
from numpy.linalg import eigh, solve
from numpy.random import randn
from matplotlib.pyplot import subplots, show

def cov(data):
    """
    Covariance matrix
    note: specifically for mean-centered data
    note: numpy's `cov` uses N-1 as normalization
    """
    return dot(X.T, X) / X.shape[0]
    # N = data.shape[1]
    # C = empty((N, N))
    # for j in range(N):
    #   C[j, j] = mean(data[:, j] * data[:, j])
    #   for k in range(j + 1, N):
    #       C[j, k] = C[k, j] = mean(data[:, j] * data[:, k])
    # return C

def pca(data, pc_count = None):
    """
    Principal component analysis using eigenvalues
    note: this mean-centers and auto-scales the data (in-place)
    """
    data -= mean(data, 0)
    data /= std(data, 0)
    C = cov(data)
    E, V = eigh(C)
    key = argsort(E)[::-1][:pc_count]
    E, V = E[key], V[:, key]
    U = dot(data, V)  # used to be dot(V.T, data.T).T
    return U, E, V

""" test data """
data = array([randn(8) for k in range(150)])
data[:50, 2:4] += 5
data[50:, 2:5] += 5

""" visualize """
trans = pca(data, 3)[0]
fig, (ax1, ax2) = subplots(1, 2)
ax1.scatter(data[:50, 0], data[:50, 1], c = 'r')
ax1.scatter(data[50:, 0], data[50:, 1], c = 'b')
ax2.scatter(trans[:50, 0], trans[:50, 1], c = 'r')
ax2.scatter(trans[50:, 0], trans[50:, 1], c = 'b')
show()

Ce qui donne la même chose que la beaucoup plus courte

from sklearn.decomposition import PCA

def pca2(data, pc_count = None):
    return PCA(n_components = 4).fit_transform(data)

Si je comprends bien, l'utilisation de valeurs propres (première façon) est préférable pour les données à haute dimension et moins d'échantillons, alors que l'utilisation de la décomposition des valeurs singulières est préférable si vous avez plus d'échantillons que de dimensions.

Ceci est un travail pour numpy.

Et voici un tutoriel montrant comment l'analyse des composants pincipaux peut être effectuée en utilisant les modules intégrés de numpy comme mean,cov,double,cumsum,dot,linalg,array,rank.

Http://glowingpython.blogspot.sg/2011/07/principal-component-analysis-with-numpy.html

Notez que scipy a aussi une longue explication ici - https://github.com/scikit-learn/scikit-learn/blob/babe4a5d0637ca172d47e1dfdd2f6f3c3ecb28db/scikits/learn/utils/extmath.py#L105

Avec le scikit-learn bibliothèque ayant plus d'exemples de code - https://github.com/scikit-learn/scikit-learn/blob/babe4a5d0637ca172d47e1dfdd2f6f3c3ecb28db/scikits/learn/utils/extmath.py#L105

Voici les options scikit-learn. Avec les deux méthodes, StandardScaler a été utilisé parce que PCA est effectuée par scale

Méthode 1: Demandez à scikit-learn de choisir le nombre minimum {[8] } de composants principaux tels qu'au moins x% (90% dans l'exemple ci-dessous) de la variance est conservé.

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

iris = load_iris()

# mean-centers and auto-scales the data
standardizedData = StandardScaler().fit_transform(iris.data)

pca = PCA(.90)

principalComponents = pca.fit_transform(X = standardizedData)

# To get how many principal components was chosen
print(pca.n_components_)

Méthode 2: Choisissez le nombre de composants principaux (dans ce cas, 2 a été choisi)

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

iris = load_iris()

standardizedData = StandardScaler().fit_transform(iris.data)

pca = PCA(n_components=2)

principalComponents = pca.fit_transform(X = standardizedData)

# to get how much variance was retained
print(pca.explained_variance_ratio_.sum())

Source: https://towardsdatascience.com/pca-using-python-scikit-learn-e653f8989e60

Mise À JOUR: matplotlib.mlab.PCA est depuis la version 2.2 (2018-03-06) en effet obsolète .

La bibliothèque matplotlib.mlab.PCA (utilisé dans cette réponse) est pas obsolète. Donc, pour tous les gens arrivant ici via Google, je vais poster un exemple de travail complet testé avec Python 2.7.

Utilisez le code suivant avec précaution car il utilise une bibliothèque maintenant obsolète!

from matplotlib.mlab import PCA
import numpy
data = numpy.array( [[3,2,5], [-2,1,6], [-1,0,4], [4,3,4], [10,-5,-6]] )
pca = PCA(data)

Maintenant dans ' pca.Y ' est la matrice de données d'origine en termes de base des composants principaux vecteur. Plus de détails sur L'objet PCA peuvent être trouvés ici .

>>> pca.Y
array([[ 0.67629162, -0.49384752,  0.14489202],
   [ 1.26314784,  0.60164795,  0.02858026],
   [ 0.64937611,  0.69057287, -0.06833576],
   [ 0.60697227, -0.90088738, -0.11194732],
   [-3.19578784,  0.10251408,  0.00681079]])

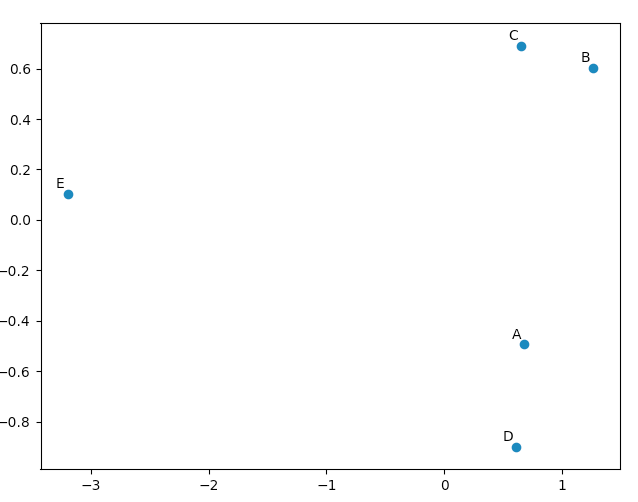
Vous pouvez utiliser matplotlib.pyplot pour dessiner ces données, juste pour vous convaincre que le PCA donne de "bons" résultats. La liste names est juste utilisée pour annoter nos cinq vecteurs.

import matplotlib.pyplot
names = [ "A", "B", "C", "D", "E" ]
matplotlib.pyplot.scatter(pca.Y[:,0], pca.Y[:,1])
for label, x, y in zip(names, pca.Y[:,0], pca.Y[:,1]):
    matplotlib.pyplot.annotate( label, xy=(x, y), xytext=(-2, 2), textcoords='offset points', ha='right', va='bottom' )
matplotlib.pyplot.show()

En regardant nos vecteurs originaux, nous verrons que data[0] ("A") et data [3] ("D") sont plutôt similaires à data[1] ("B") et data[2] ("C"). Cela se reflète dans le tracé 2D de notre PCA transformé données.

J'ai fait un petit script pour comparer les différents PCA est apparu comme une réponse ici:

import numpy as np
from scipy.linalg import svd

shape = (26424, 144)
repeat = 20
pca_components = 2

data = np.array(np.random.randint(255, size=shape)).astype('float64')

# data normalization
# data.dot(data.T)
# (U, s, Va) = svd(data, full_matrices=False)
# data = data / s[0]

from fbpca import diffsnorm
from timeit import default_timer as timer

from scipy.linalg import svd
start = timer()
for i in range(repeat):
    (U, s, Va) = svd(data, full_matrices=False)
time = timer() - start
err = diffsnorm(data, U, s, Va)
print('svd time: %.3fms, error: %E' % (time*1000/repeat, err))


from matplotlib.mlab import PCA
start = timer()
_pca = PCA(data)
for i in range(repeat):
    U = _pca.project(data)
time = timer() - start
err = diffsnorm(data, U, _pca.fracs, _pca.Wt)
print('matplotlib PCA time: %.3fms, error: %E' % (time*1000/repeat, err))

from fbpca import pca
start = timer()
for i in range(repeat):
    (U, s, Va) = pca(data, pca_components, True)
time = timer() - start
err = diffsnorm(data, U, s, Va)
print('facebook pca time: %.3fms, error: %E' % (time*1000/repeat, err))


from sklearn.decomposition import PCA
start = timer()
_pca = PCA(n_components = pca_components)
_pca.fit(data)
for i in range(repeat):
    U = _pca.transform(data)
time = timer() - start
err = diffsnorm(data, U, _pca.explained_variance_, _pca.components_)
print('sklearn PCA time: %.3fms, error: %E' % (time*1000/repeat, err))

start = timer()
for i in range(repeat):
    (U, s, Va) = pca_mark(data, pca_components)
time = timer() - start
err = diffsnorm(data, U, s, Va.T)
print('pca by Mark time: %.3fms, error: %E' % (time*1000/repeat, err))

start = timer()
for i in range(repeat):
    (U, s, Va) = pca_doug(data, pca_components)
time = timer() - start
err = diffsnorm(data, U, s[:pca_components], Va.T)
print('pca by doug time: %.3fms, error: %E' % (time*1000/repeat, err))

Pca_mark est le pca dans la réponse de Mark .

Pca_doug est le pca dans la réponse de doug .

Voici un exemple de sortie (mais le résultat dépend beaucoup de la taille des données et de pca_components, donc je recommande d'exécuter votre propre test avec vos propres données. En outre, le pca de facebook est optimisé pour les données normalisées, il sera donc plus rapide et plus précis cas):

svd time: 3212.228ms, error: 1.907320E-10
matplotlib PCA time: 879.210ms, error: 2.478853E+05
facebook pca time: 485.483ms, error: 1.260335E+04
sklearn PCA time: 169.832ms, error: 7.469847E+07
pca by Mark time: 293.758ms, error: 1.713129E+02
pca by doug time: 300.326ms, error: 1.707492E+02

Modifier:

La fonction diffsnorm de fbpca calcule l'erreur de norme spectrale d'une décomposition de Schur.

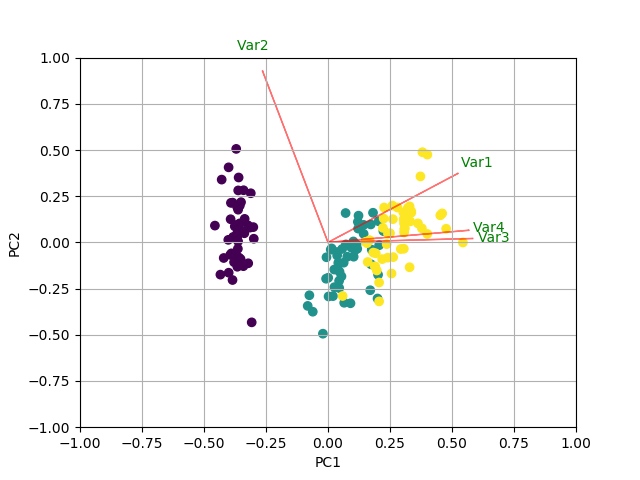
En plus de toutes les autres réponses, voici du code pour tracer le biplot en utilisant sklearn et matplotlib.

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
import pandas as pd
from sklearn.preprocessing import StandardScaler

iris = datasets.load_iris()
X = iris.data
y = iris.target
#In general a good idea is to scale the data
scaler = StandardScaler()
scaler.fit(X)
X=scaler.transform(X)    

pca = PCA()
x_new = pca.fit_transform(X)

def myplot(score,coeff,labels=None):
    xs = score[:,0]
    ys = score[:,1]
    n = coeff.shape[0]
    scalex = 1.0/(xs.max() - xs.min())
    scaley = 1.0/(ys.max() - ys.min())
    plt.scatter(xs * scalex,ys * scaley, c = y)
    for i in range(n):
        plt.arrow(0, 0, coeff[i,0], coeff[i,1],color = 'r',alpha = 0.5)
        if labels is None:
            plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, "Var"+str(i+1), color = 'g', ha = 'center', va = 'center')
        else:
            plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, labels[i], color = 'g', ha = 'center', va = 'center')
plt.xlim(-1,1)
plt.ylim(-1,1)
plt.xlabel("PC{}".format(1))
plt.ylabel("PC{}".format(2))
plt.grid()

#Call the function. Use only the 2 PCs.
myplot(x_new[:,0:2],np.transpose(pca.components_[0:2, :]))
plt.show()

Pour l'amour def plot_pca(data): fonctionne, il est nécessaire de remplacer les lignes

data_resc, data_orig = PCA(data)
ax1.plot(data_resc[:, 0], data_resc[:, 1], '.', mfc=clr1, mec=clr1)

Avec des lignes

newData, data_resc, data_orig = PCA(data)
ax1.plot(newData[:, 0], newData[:, 1], '.', mfc=clr1, mec=clr1)