Quelle est la relation entre le nombre de Vecteurs de Support et les données de formation et la performance des classificateurs?
j'utilise LibSVM pour classer certains documents. Les documents semblent être un peu difficile de classer dans les résultats finaux montrent. Cependant, j'ai remarqué quelque chose lors de la formation de mes modèles. et qui est: Si ma formation est par exemple 1000 environ 800 d'entre eux sont sélectionnés en tant que vecteurs de soutien. J'ai cherché partout si c'était une bonne ou une mauvaise chose. Y a-t-il une relation entre le nombre de vecteurs de support et la performance des classificateurs? J'ai lu ce post post précédent . Cependant, j'effectue une sélection de paramètres et je suis sûr que les attributs dans les vecteurs de fonctionnalités sont tous ordonnés. J'ai juste besoin de connaître la relation. Grâce. p.s: j'utilise un noyau linéaire.
5 réponses
sont un problème d'optimisation. Ils tentent de trouver un hyperplan qui divise les deux classes avec la plus grande marge. Les vecteurs de support sont les points qui se situent dans cette marge. C'est plus facile à comprendre si vous le construisez de simple à plus complexe.
Dur Marge Linéaire SVM
dans un ensemble d'entraînement a où les données sont linéairement séparables, et vous utilisez une marge dure (aucun mou n'est autorisé), les vecteurs de support sont les points qui se trouvent le long des hyperplanes de support (les hyperplanes parallèles à l'hyperplan divisant aux bords de la marge)
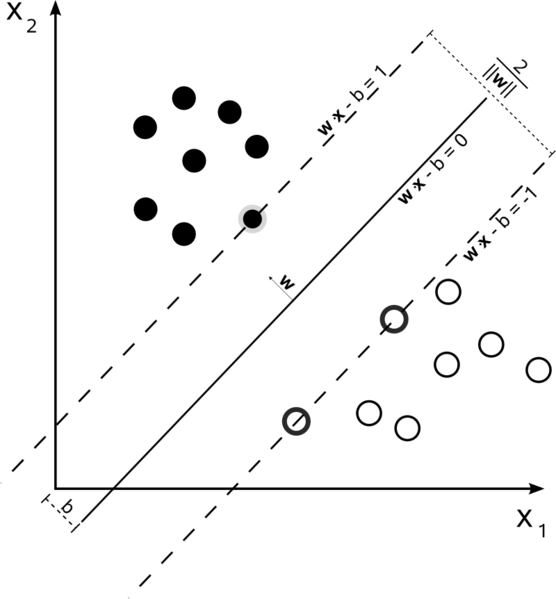
tous les vecteurs de support se trouvent exactement sur la marge. Peu importe le nombre de dimensions ou la taille de l'ensemble de données, le nombre de vecteurs de support pourrait être aussi faible que 2.
Soft-Marge SVM Linéaire
mais que faire si notre ensemble de données n'est pas linéairement séparable? Nous introduisons le SVM de marge souple. Nous n'exigeons plus que nos points de données se trouvent en dehors de la marge, nous permettons à une certaine quantité d'entre eux de s'écarter de la ligne dans la marge. Nous utilisons le paramètre slack C pour contrôler cela. (nu dans nu-SVM) cela nous donne une marge plus large et une plus grande erreur sur l'ensemble de données de formation, mais améliore la généralisation et/ou nous permet de trouver une séparation linéaire des données qui n'est pas linéaire séparable.
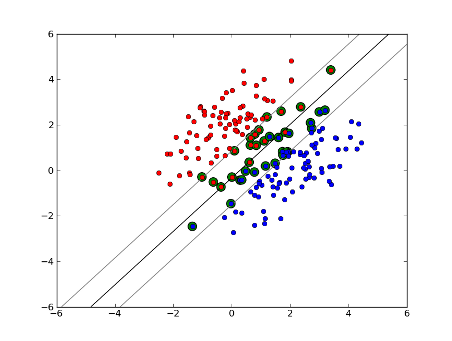
maintenant, le nombre de vecteurs de soutien dépend de combien de mou nous permettons et la distribution des données. Si nous laissons une grande quantité de mou, nous aurons un grand nombre de vecteurs de soutien. Si nous permettons très peu de mou, nous aurons très peu de vecteurs de soutien. L'exactitude dépend de la détermination du bon niveau de jeu pour les données analysées. Il ne sera pas possible d'obtenir un niveau élevé de précision, nous devons simplement trouver le meilleur ajustement que nous le pouvons.
Non-Linéaire SVM
cela nous amène à SVM non linéaire. Nous essayons toujours de diviser linéairement les données, mais nous essayons maintenant de le faire dans un espace dimensionnel supérieur. Cela se fait via une fonction du noyau, qui a bien sûr son propre ensemble de paramètres. Lorsque nous traduisons ce retour à l'espace original, le résultat est non linéaire:
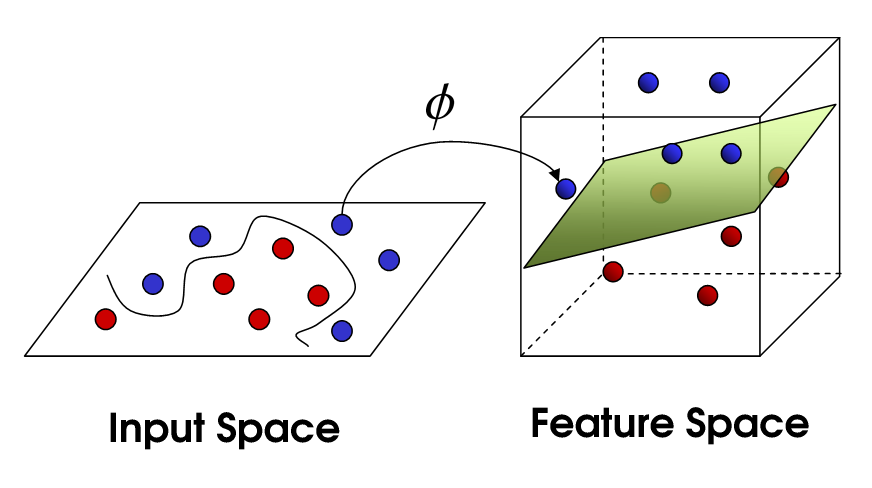
maintenant, le nombre de vecteurs de support dépend encore de la marge de manouvre que nous autorisons, mais il dépend aussi de la complexité de notre modèle. Chaque tordre et tourner dans le modèle final dans notre espace d'entrée nécessite un ou plusieurs vecteurs de soutien à définir. En fin de compte, la sortie D'un SVM est constituée des vecteurs de support et d'un alpha, qui définit essentiellement l'influence de ce vecteur de support spécifique sur la décision finale.
ici, l'exactitude dépend du compromis entre un modèle très complexe qui peut SUR-ajuster les données et une marge importante qui classera incorrectement certaines données de formation dans l'intérêt d'une meilleure généralisation. Le nombre de vecteurs de support peut varier de très peu à chaque point de données si vous complétez vos données. Ce compromis est contrôlé par C et par le choix des paramètres du noyau et du noyau.
je suppose que quand vous avez dit performance vous étiez pour ce qui est de la précision, mais j'ai pensé que je parlerais aussi de la performance en termes de complexité computationnelle. Pour tester un point de données à l'aide d'un modèle SVM, vous devez calculer le produit dot de chaque vecteur de support avec le point de test. Par conséquent, la complexité computationnelle du modèle est linéaire dans le nombre de vecteurs de soutien. Moins de vecteurs de soutien signifie une classification plus rapide des points d'essai.
une bonne ressource: un tutoriel sur les machines vectorielles de Support pour la reconnaissance de modèle
800 Sur 1000 vous dit essentiellement que le SVM doit utiliser presque chaque échantillon de formation pour coder l'ensemble de formation. Cela vous indique qu'il n'y a pas beaucoup de régularité dans vos données.
semble comme vous avez des problèmes majeurs avec pas assez de données de formation. Aussi, peut-être penser à certaines caractéristiques spécifiques qui séparent ces données mieux.
les deux nombre d'échantillons et nombre d'attributs mai influencent le nombre de vecteurs de support, ce qui rend le modèle plus complexe. Je crois que vous utilisez des mots ou même des ngrams comme attributs, donc il y en a beaucoup, et les modèles de langage naturel sont eux-mêmes très complexes. Ainsi, 800 Vecteurs de support de 1000 échantillons semblent être ok. (Faites également attention aux commentaires de @karenu sur les paramètres C / nu qui ont également de grandes effet sur le nombre de SVs).
pour avoir une intuition sur cette idée principale SVM de rappel. SVM travaille dans un espace de caractéristiques multidimensionnel et tente de trouver hyperplane qui sépare tous les échantillons donnés. Si vous avez beaucoup d'échantillons et seulement 2 fonctions (2 dimensions), les données et hyperplane peut ressembler à ceci:
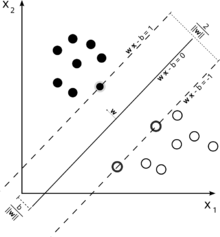
ici il n'y a que 3 Vecteurs de soutien, tous les autres sont derrière eux et donc ne jouent aucun rôle. Notez que ces vecteurs sont définies par seulement 2 coordonnées.
imaginez maintenant que vous avez un espace tridimensionnel et que les vecteurs de support sont définis par 3 coordonnées.
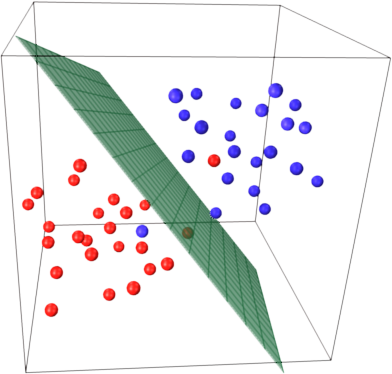
cela signifie qu'il y a encore un paramètre (coordonnée) à ajuster, et ce réglage peut nécessiter plus d'échantillons pour trouver l'hyperplan optimal. En d'autres termes, dans dans le pire des cas, SVM ne trouve qu'une coordonnée hyperplan par échantillon.
lorsque les données sont bien structurées (c.-à - d. qu'elles sont assez stables), seuls plusieurs vecteurs de soutien peuvent être nécessaires-tous les autres resteront derrière eux. Mais le texte est très mal structuré de données. SVM fait de son mieux, en essayant d'ajuster l'échantillon aussi bien que possible, et prend ainsi comme vecteurs de soutien encore plus d'échantillons que de gouttes. Avec l'augmentation du nombre d'échantillons, cette "anomalie" est réduite (des échantillons plus insignifiants le nombre absolu de vecteurs de support reste très élevé.
classification SVM est linéaire en le nombre de vecteurs de soutien (SVs). Le nombre de SVs est dans le pire des cas égal au nombre d'échantillons de formation, donc 800/1000 n'est pas encore le pire des cas, mais c'est encore assez mauvais.
encore une fois, 1000 documents de formation est un petit ensemble de formation. Vous devriez vérifier ce qui se passe lorsque vous mettez à l'échelle jusqu'à 10000 ou plus de documents. Si les choses ne s'améliorent pas, envisagez d'utiliser des SVM linéaires, formés avec LibLinear , pour la classification des documents; ceux-ci se dimensionnent beaucoup mieux (la taille du modèle et le temps de classification sont linéaires dans le nombre de caractéristiques et indépendants du nombre d'échantillons de formation).
il y a une certaine confusion entre les sources. Dans le manuel ISLR 6th Ed, par exemple, C est décrit comme un "budget de violation des limites" d'où il s'ensuit que c supérieur permettra plus de violations des limites et plus de vecteurs de soutien. Mais dans les implémentations svm en R et python, le paramètre C est implémenté comme "sanction de violation", ce qui est le contraire, et vous constaterez que pour des valeurs plus élevées de C, il y a moins de vecteurs de support.