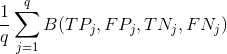Précision / rappel pour la classification multiclasse-multicabel

je me demande comment calculer les mesures de précision et de rappel pour la classification Multiclass multicabel, c.-à-d. la classification où il y a plus de deux étiquettes, et où chaque instance peut avoir plusieurs étiquettes?

21
demandé sur phoxis 2012-01-25 18:19:05

5 réponses

pour la classification à étiquettes multiples, il y a deux façons de procéder D'abord envisager la suite.

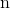  • $n$ est le nombre d'exemples.
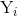  • $Y_i$ est-ce que l'étiquette de vérité de terrain est assignée 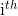$i^{th}$ exemple..
  • $x_i$ est le $i^{th}$ exemple.
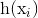  • $h(x_i)$ est-ce que les étiquettes prédites pour 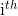$i^{th}$ exemple.

Exemple

les paramètres sont calculés par point de données. Pour chaque étiquette prédite son seul son score est calculé, puis ces scores sont agrégés sur tous les points de données.

  • précision = $\frac{1}{n}\sum_{i=1}^{n}\frac{|Y_{i}\cap h(x_{i})|}{|h(x_{i})|}$ , Le rapport de combien de la prévision est correcte. Le numérateur trouve combien d'étiquettes dans le vecteur prédit a en commun avec la vérité au sol, et le rapport calcule, combien de vraies étiquettes prédites sont en fait dans la vérité au sol.
  • Rappel = 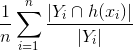$\frac{1}{n}\sum_{i=1}^{n}\frac{|Y_{i}\cap h(x_{i})|}{|Y_{i}|}$ , Le rapport du nombre des étiquettes réelles ont été prédire. Le numérateur trouve combien d'étiquettes dans le vecteur prédit a en commun avec la vérité de fond (comme ci-dessus), puis trouve le rapport au nombre d'étiquettes réelles, donc obtenir quelle fraction des étiquettes réelles ont été prédites.

il y a aussi d'autres mesures.

Label

Ici, les choses sont faites étiquettes-sage. Pour chaque étiquette, les paramètres (p. ex. précision, rappel) sont calculés et puis ces étiquette sage mesures sont agrégées. Par conséquent, dans ce cas, vous finissez par calculer la précision/rappel pour chaque étiquette sur l'ensemble des données, comme vous le faites pour une classification binaire (comme chaque étiquette a une assignation binaire), puis agréger.

la manière simple est de présenter la forme générale.

c'est juste une extension de l'équivalent multi-classe standard.

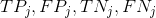  • Macro average average $\frac{1}{q}\sum_{j=1}^{q}B(TP_{j},FP_{j},TN_{j},FN_{j})$

  • Micro moyenne $B(\sum_{j=1}^{q}TP_{j},\sum_{j=1}^{q}FP_{j},\sum_{j=1}^{q}TN_{j},\sum_{j=1}^{q}FN_{j})$

ici le $TP_{j},FP_{j},TN_{j},FN_{j}$ les chiffres sont-ils respectivement vrai positif, faux positif, vrai négatif et faux négatif pour 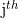$j^{th}$ étiquette .

Ici $ B$ représente n'importe quelle métrique basée sur la matrice de confusion. Dans votre cas, vous brancheriez les formules standard de précision et de rappel. Pour la macro moyenne vous passez dans le compte par étiquette et puis la somme, pour la micro moyenne vous moyenne les comptes d'abord, puis appliquer votre fonction métrique.

vous pourriez être intéressé d'avoir un coup d'oeil dans le code pour le mult-label metrics ici , qu'une partie du paquet mldr dans R . Aussi, vous pourriez être intéressé à regarder dans la bibliothèque Java multi-label MULAN .

c'est un beau papier pour entrer dans les différents paramètres: une revue sur les algorithmes D'apprentissage multi-Label

15
répondu phoxis 2016-09-09 21:42:15

la réponse est que vous devez calculer la précision et le rappel pour chaque classe, puis la moyenne ensemble. Par exemple: si vous classez A, B, et C, alors votre précision est: 

(precision(A) + precision(B) + precision(C)) / 3

idem pour rappel.

Je ne suis pas un expert, mais c'est ce que j'ai déterminé sur la base des sources suivantes:

https://list.scms.waikato.ac.nz/pipermail/wekalist/2011-March/051575.html http://stats.stackexchange.com/questions/21551/how-to-compute-precision-recall-for-multiclass-multilabel-classification

7
répondu Mark E. Haase 2012-05-13 23:46:59
  • supposons que nous avons un problème de classement multiple en 3 classes avec les étiquettes A, B et C.
  • La première chose à faire est de générer une matrice de confusion. Notez que les valeurs de la diagonale sont toujours les vrais positifs (TP).

  • maintenant, pour calculer rappel pour l'étiquette a, vous pouvez lire les valeurs de la matrice de confusion et de calculer: 

    = TP_A/(TP_A+FN_A)
= TP_A/(Total gold labels for A)

  • maintenant, calculons précision pour l'étiquette a, vous pouvez lire les valeurs de la matrice de confusion et calculer: 

    = TP_A/(TP_A+FP_A)
= TP_A/(Total predicted as A)

  • il suffit de faire la même chose pour les autres étiquettes B et C. Ceci s'applique à tout problème de classification multi-classes.

Ici est l'article qui parle de la façon de calculer la précision et le rappel pour tout problème de classification à classes multiples, y compris les exemples.

4
répondu kavgan 2014-10-23 20:55:26

une Simple moyenne va faire si les classes sont équilibrées.

sinon, le rappel pour chaque classe réelle doit être pondéré par la prévalence de la classe, et la précision pour chaque étiquette prédite doit être pondérée par le biais (probabilité) pour chaque étiquette. Vous pouvez également obtenir Rand Précision.

une façon plus directe est de faire une table de contingence normalisée (diviser par N donc table additionne jusqu'à 1 pour chaque combinaison de l'étiquette et de la classe) et ajouter le diagonale pour obtenir la précision de Rand.

mais si les classes ne sont pas équilibrées, le biais reste et une méthode corrigée par chance telle que kappa est plus appropriée, ou mieux encore l'analyse ROC ou une mesure correcte par chance telle que l'informedness (hauteur au-dessus de la ligne de chance dans ROC).

0
répondu David M W Powers 2015-03-20 07:18:58

en python en utilisant sklearn et numpy : 

from sklearn.metrics import confusion_matrix
import numpy as np

labels = ...
predictions = ...

cm = confusion_matrix(labels, predictions)
recall = np.diag(cm) / np.sum(cm, axis = 1)
precision = np.diag(cm) / np.sum(cm, axis = 0)
0
répondu Cristian Garcia 2018-08-22 22:52:26