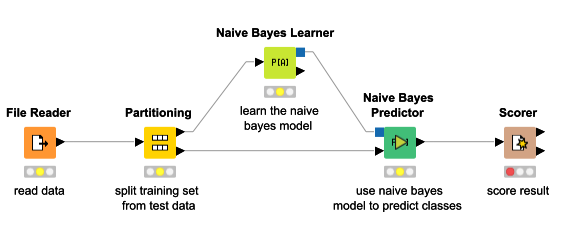
Une explication simple de la classification naïve de Bayes
J'ai du mal à comprendre le processus de Bayes naïfs, et je me demandais si quelqu'un pouvait l'expliquer avec un processus simple étape par étape en anglais. Je comprends qu'il faut des comparaisons par moments comme une probabilité, mais je n'ai aucune idée de la façon dont les données d'entraînement sont liées à l'ensemble de données réel.
Veuillez me donner une explication du rôle que joue l'ensemble de formation. Je donne un exemple très simple pour les fruits comme la banane par exemple
training set---
round-red
round-orange
oblong-yellow
round-red
dataset----
round-red
round-orange
round-red
round-orange
oblong-yellow
round-red
round-orange
oblong-yellow
oblong-yellow
round-red
5 réponses
Votre question, si je comprends bien, est divisée en deux parties. L'un étant que vous avez besoin de plus de compréhension pour le classificateur Bayes naïf et le second étant la confusion entourant L'ensemble de formation.
En général, tous les algorithmes D'apprentissage automatique doivent être formés pour des tâches d'apprentissage supervisées telles que la classification,la prédiction, etc. ou pour des tâches d'apprentissage non supervisées comme le clustering.
Par la formation, cela signifie les former sur des intrants particuliers afin que plus tard, nous puissions les tester pour Inconnu entrées (qu'ils n'ont jamais vues auparavant) pour lesquelles ils peuvent classer ou prédire etc (en cas d'apprentissage supervisé) en fonction de leur apprentissage. C'est ce que la plupart des techniques D'apprentissage automatique comme les réseaux de neurones, SVM, bayésien, etc. sont basées sur.
Donc, dans un projet général D'apprentissage automatique, vous devez diviser votre ensemble d'entrée en un ensemble de développement ( ensemble D'entraînement + ensemble de test Dev) et un ensemble de Test (ou ensemble D'évaluation). Rappelez-vous que votre objectif de base serait que votre système apprend et classe les nouvelles entrées qu'ils n'ont jamais vues auparavant dans un ensemble de développement ou un ensemble de test.
L'ensemble de test a généralement le même format que l'ensemble de la formation. Cependant, il est très important que l'ensemble de tests soit distinct du corpus de formation: si nous réutilisé l'ensemble de formation comme l'ensemble de test, puis un modèle qui simplement mémorisé son entrée, sans apprendre à généraliser à de nouveaux exemples, recevrait des scores trompeusement élevés.
En général, par exemple, 70% peut être des cas de formation. Rappelez-vous également de partitionner l'ensemble d'origine dans les ensembles d'entraînement et de test au hasard .
Maintenant, j'en viens à votre autre question sur naïf Bayes.
Source de l'exemple ci-dessous: http://www.statsoft.com/textbook/naive-bayes-classifier
Pour démontrer le concept de classification Naïve de Bayes, considérons l'exemple donné ci-dessous:
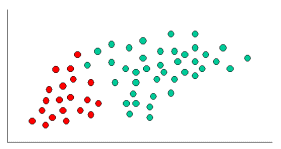
Comme indiqué, les objets peuvent être classés comme soit GREEN ou RED. Notre tâche est de classer les nouveaux cas à mesure qu'ils arrivent, c'est-à-dire de décider à quelle étiquette de classe ils appartiennent, en fonction des objets existants.
Comme il y a deux fois plus d'objets GREEN que RED , Il est raisonnable de croire qu'un nouveau cas (qui n'a pas encore été observé) est deux fois plus susceptible d'avoir une appartenance GREEN plutôt que RED. Dans L'analyse bayésienne, cette croyance est connue sous le nom de probabilité antérieure. Les probabilités antérieures sont basées sur l'expérience antérieure, dans ce cas, le pourcentage d'objets GREEN et RED, et souvent utilisé pour prédire les résultats avant qu'ils ne se produisent réellement.
Ainsi, nous pouvons écrire:
Avant de Probabilité de GREEN: number of GREEN objects / total number of objects
Avant de Probabilité de RED: number of RED objects / total number of objects
Comme il y a un total d'objets 60, 40 dont GREEN et 20 RED, Nos probabilités antérieures d'appartenance à une classe sont:
Probabilité antérieure pour GREEN : 40 / 60
Avant de Probabilité pour RED: 20 / 60
Après avoir formulé notre probabilité antérieure, nous sommes maintenant prêts à classer un nouvel objet (WHITE cercle dans le diagramme ci-dessous). Puisque les objets sont bien regroupés, il est raisonnable de supposer que plus il y a d'objets GREEN (ou RED) à proximité de X, plus les nouveaux cas sont susceptibles d'appartenir à cette couleur particulière. Pour mesurer cette probabilité, nous dessinons un cercle autour de X qui englobe un nombre (à choisir un priori) de points indépendamment de leurs étiquettes de classe. Ensuite, nous calculons le nombre de points dans le cercle appartenant à chaque étiquette de classe. A partir de là, nous calculons la probabilité:
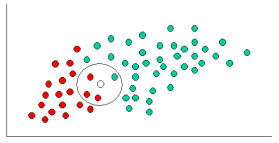
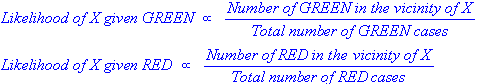
D'après l'illustration ci-dessus, il est clair que la probabilité de X donnée GREEN est inférieure à la probabilité de X donnée RED, puisque le cercle englobe 1 GREEN objet et 3 RED les uns. Ainsi:
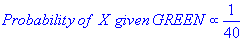
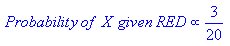
Bien que les probabilités antérieures indiquent que X appartiennent à GREEN (étant donné qu'il y a deux fois plus de GREEN par rapport à RED) la probabilité indique le contraire; que l'appartenance à une catégorie de X est RED (étant donné qu'il y a plus de RED des objets dans le voisinage de X que GREEN). Dans L'analyse bayésienne, la classification finale est produite en combinant les deux sources d'information, c'est-à-dire l'avant et la probabilité, pour former une probabilité postérieure en utilisant la règle dite de Bayes (nommée D'après le révérend Thomas Bayes 1702-1761).

Enfin, nous classons X comme RED puisque son appartenance à la classe atteint la plus grande probabilité postérieure.
Je me rends compte que c'est une vieille question, avec une réponse. La raison pour laquelle je poste est que la réponse acceptée a beaucoup d'éléments de k-NN ( k - les voisins les plus proches), un algorithme différent.
K-NN et NaiveBayes sont des algorithmes de classification. Conceptuellement, k-NN utilise l'idée de "proximité" pour classer de nouvelles entités. En k-NN, la "proximité" est modélisée avec des idées telles que la Distance euclidienne ou la Distance cosinus. En revanche, dans NaiveBayes, le concept de la "probabilité" est utilisée pour classer les nouvelles entités.
Puisque la question concerne naïf Bayes, voici comment je décrirais les idées et les étapes à quelqu'un. Je vais essayer de le faire avec aussi peu d'équations et en anglais clair autant que possible.
Tout D'Abord, La Probabilité Conditionnelle Et La Règle De Bayes
Avant que quelqu'un puisse comprendre et apprécier les nuances de naïf Bayes', ils ont besoin de connaître quelques concepts connexes d'abord, à savoir, l'idée de probabilité conditionnelle, et Bayes' Règle. (Si vous êtes familier avec ces concepts, passez à la section intitulée se rendre à Naive Bayes')
Probabilité conditionnelle {[29] } en anglais simple: Quelle est la probabilité que quelque chose se produise, étant donné que quelque chose d'autre est déjà arrivé.
Disons qu'il y a un résultat O. et une preuve E. de la façon dont ces probabilités sont définies: la probabilité d'avoir à la fois le résultat O et la preuve E est: (Probabilité de o se produisant) multiplié par le (Prob de E étant donné que O s'est produit)
Un Exemple pour comprendre Probabilité Conditionnelle:
Disons que nous avons une collection de sénateurs américains. Les sénateurs pourraient être démocrates ou républicains. Ils sont aussi des hommes ou des femmes.
Si nous sélectionnons un sénateur complètement au hasard, Quelle est la probabilité que cette personne soit une femme Démocrate? Probabilité conditionnelle peut nous aider à répondre à cela.
Probabilité de (Démocrate et sénatrice) = Prob (le sénateur est Démocrate) multiplié par la probabilité conditionnelle d'être une femme étant donné qu'ils sont démocrates.
P(Democrat & Female) = P(Democrat) * P(Female | Democrat)
Nous pourrions calculer exactement la même chose, de la manière inverse:
P(Democrat & Female) = P(Female) * P(Democrat | Female)
Comprendre La Règle De Bayes
Conceptuellement, c'est une façon de passer de P(preuve| résultat connu) à P(résultat|preuve connue). Souvent, nous savons à quelle fréquence certaines preuves particulières sont observées, étant donné un résultat connu . Nous devons utiliser cette fait connu pour calculer l'inverse, pour calculer la chance que ce résultat se produise , compte tenu de la preuve.
P(résultat étant donné que nous connaissons certaines preuves) = P (preuve étant donné que nous connaissons le résultat) fois Prob (résultat), mis à l'échelle par le P (preuve)
L'exemple classique pour comprendre la règle de Bayes:
Probability of Disease D given Test-positive =
Prob(Test is positive|Disease) * P(Disease)
_______________________________________________________________
(scaled by) Prob(Testing Positive, with or without the disease)
Maintenant, tout cela n'était que préambule, pour arriver à naïve Bayes.
Arriver à Naïf de Bayes
Jusqu'à présent, nous n'avons parlé que d'un seul morceau de preuve. En réalité, nous devons prédire un résultat donné plusieurs preuves., Dans ce cas, le calcul devient très compliqué. Pour contourner cette complication, une approche consiste à "découpler" plusieurs éléments de preuve et à traiter chaque élément de preuve comme indépendant. Cette approche est la raison pour laquelle cela est appelé naïf Bayes.
P(Outcome|Multiple Evidence) =
P(Evidence1|Outcome) * P(Evidence2|outcome) * ... * P(EvidenceN|outcome) * P(Outcome)
scaled by P(Multiple Evidence)
Beaucoup de gens choisissent de se souvenir de ceci comme:
P(Likelihood of Evidence) * Prior prob of outcome
P(outcome|evidence) = _________________________________________________
P(Evidence)
Remarquez quelques choses sur cette équation:
- si le Prob (preuve|résultat) est 1, alors nous ne faisons que multiplier par 1.
- si le Prob (une preuve|résultat particulier) est 0, alors le prob entier. devient 0. Si vous voyez des preuves contradictoires, nous pouvons exclure ce résultat.
- puisque nous divisons tout par P(preuve), nous pouvons même nous en sortir sans le calculer.
- l'intuition derrière la multiplication par le précédent {[19] } est de sorte que nous donnons une forte probabilité à des résultats plus communs, et de faibles probabilités à improbable résultat. Ceux-ci sont également appelés
base rateset ils sont un moyen de mettre à l'échelle nos probabilités prédites.
Comment appliquer NaiveBayes pour prédire un résultat?
Exécutez simplement la formule ci-dessus pour chaque résultat possible. Depuis que nous essayons de classer, chaque résultat est appelé class et a class label. Notre travail est d'examiner les preuves, d'examiner comment il est susceptible d'être de cette catégorie ou de cette classe, et d'attribuer une étiquette à chaque entité.
Encore une fois, nous adoptons une approche très simple: La classe qui a la probabilité la plus élevée est déclarée "gagnante" et cette étiquette de classe est attribuée à cette combinaison de preuves.
Exemple De Fruit
Essayons sur un exemple pour améliorer notre compréhension: le PO a demandé un exemple d'identification de "fruit".
Disons que nous avons des données sur 1000 morceaux de fruits. Ils se trouvent être Banane, Orange ou certains Autres Fruits. Nous connaissons 3 caractéristiques sur chacun fruits:
- Si elle est Longue
- si elle est douce et
- si sa couleur est jaune.
C'est notre ensemble d'entraînement."Nous allons l'utiliser pour prédire le type de tout nouveaux fruits que nous rencontrons.
Type Long | Not Long || Sweet | Not Sweet || Yellow |Not Yellow|Total
___________________________________________________________________
Banana | 400 | 100 || 350 | 150 || 450 | 50 | 500
Orange | 0 | 300 || 150 | 150 || 300 | 0 | 300
Other Fruit | 100 | 100 || 150 | 50 || 50 | 150 | 200
____________________________________________________________________
Total | 500 | 500 || 650 | 350 || 800 | 200 | 1000
___________________________________________________________________
Nous pouvons pré-calculer beaucoup de choses sur notre collection de fruits.
Les probabilités dites "antérieures". (Si nous ne connaissions aucun des attributs des fruits, ce serait notre hypothèse.) Ce sont nos base rates.
P(Banana) = 0.5 (500/1000)
P(Orange) = 0.3
P(Other Fruit) = 0.2
Probabilité de "preuve"
p(Long) = 0.5
P(Sweet) = 0.65
P(Yellow) = 0.8
Probabilité de "Probabilité"
P(Long|Banana) = 0.8
P(Long|Orange) = 0 [Oranges are never long in all the fruit we have seen.]
....
P(Yellow|Other Fruit) = 50/200 = 0.25
P(Not Yellow|Other Fruit) = 0.75
Compte tenu d'un Fruit, comment le classer?
Disons qu'on nous donne les propriétés d'un fruit inconnu, et qu'on nous demande de le classer. On nous dit que le fruit est Long, doux et jaune. Est-ce une Banane? Est-il Orange? Ou est-ce un autre Fruit?
, Nous pouvons simplement les chiffres pour chacun des 3 résultats, un par un. Ensuite, nous choisissons la probabilité la plus élevée et "classifiez" notre fruit inconnu comme appartenant à la classe qui avait la probabilité la plus élevée sur la base de nos preuves antérieures (notre ensemble de formation de fruits 1000):
P(Banana|Long, Sweet and Yellow)
P(Long|Banana) * P(Sweet|Banana) * P(Yellow|Banana) * P(banana)
= _______________________________________________________________
P(Long) * P(Sweet) * P(Yellow)
= 0.8 * 0.7 * 0.9 * 0.5 / P(evidence)
= 0.252 / P(evidence)
P(Orange|Long, Sweet and Yellow) = 0
P(Other Fruit|Long, Sweet and Yellow)
P(Long|Other fruit) * P(Sweet|Other fruit) * P(Yellow|Other fruit) * P(Other Fruit)
= ____________________________________________________________________________________
P(evidence)
= (100/200 * 150/200 * 50/200 * 200/1000) / P(evidence)
= 0.01875 / P(evidence)
Par une marge écrasante (0.252 >> 0.01875), nous classons ce fruit sucré / Long / jaune comme susceptible d'être une banane.
Pourquoi le classificateur Bayes est-il si populaire?
Regardez ce que cela finit par devenir. Juste un peu de comptage et de multiplication. Nous pouvons pré-calculer tous ces Termes, et ainsi classer devient facile, rapide et efficace.
Let z = 1 / P(evidence). Maintenant, nous calculons rapidement les trois quantités suivantes.
P(Banana|evidence) = z * Prob(Banana) * Prob(Evidence1|Banana) * Prob(Evidence2|Banana) ...
P(Orange|Evidence) = z * Prob(Orange) * Prob(Evidence1|Orange) * Prob(Evidence2|Orange) ...
P(Other|Evidence) = z * Prob(Other) * Prob(Evidence1|Other) * Prob(Evidence2|Other) ...
Attribuez l'étiquette de classe du nombre le plus élevé, et vous avez terminé.
Malgré le nom, Naive Bayes s'avère excellent dans certaines applications. La classification du texte est un domaine où elle brille vraiment.
J'espère que cela aide à comprendre les concepts derrière L'algorithme naïf de Bayes.
Ram Narasimhan a très bien expliqué le concept voici ci-dessous une explication alternative à travers l'exemple de code de Naive Bayes in action
Il utilise un exemple de problème de ce livre à la page 351
C'est l'ensemble de données que nous allons utiliser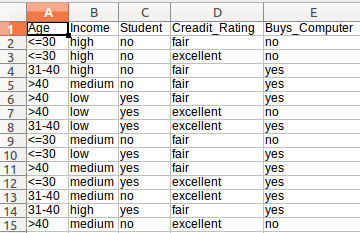
Dans l'ensemble de données ci-dessus si nous donnons l'hypothèse = {"Age":'<=30', "Income":"medium", "Student":'yes' , "Creadit_Rating":'fair'} alors quelle est la probabilité qu'il achètera ou n'achètera pas un ordinateur.
Le code ci-dessous répond exactement à cette question.
Il suffit de créer un fichier appelé nommé new_dataset.csv et collez le contenu suivant.
Age,Income,Student,Creadit_Rating,Buys_Computer
<=30,high,no,fair,no
<=30,high,no,excellent,no
31-40,high,no,fair,yes
>40,medium,no,fair,yes
>40,low,yes,fair,yes
>40,low,yes,excellent,no
31-40,low,yes,excellent,yes
<=30,medium,no,fair,no
<=30,low,yes,fair,yes
>40,medium,yes,fair,yes
<=30,medium,yes,excellent,yes
31-40,medium,no,excellent,yes
31-40,high,yes,fair,yes
>40,medium,no,excellent,no
Voici le code que les commentaires expliquent tout ce que nous faisons ici! [python]
import pandas as pd
import pprint
class Classifier():
data = None
class_attr = None
priori = {}
cp = {}
hypothesis = None
def __init__(self,filename=None, class_attr=None ):
self.data = pd.read_csv(filename, sep=',', header =(0))
self.class_attr = class_attr
'''
probability(class) = How many times it appears in cloumn
__________________________________________
count of all class attribute
'''
def calculate_priori(self):
class_values = list(set(self.data[self.class_attr]))
class_data = list(self.data[self.class_attr])
for i in class_values:
self.priori[i] = class_data.count(i)/float(len(class_data))
print "Priori Values: ", self.priori
'''
Here we calculate the individual probabilites
P(outcome|evidence) = P(Likelihood of Evidence) x Prior prob of outcome
___________________________________________
P(Evidence)
'''
def get_cp(self, attr, attr_type, class_value):
data_attr = list(self.data[attr])
class_data = list(self.data[self.class_attr])
total =1
for i in range(0, len(data_attr)):
if class_data[i] == class_value and data_attr[i] == attr_type:
total+=1
return total/float(class_data.count(class_value))
'''
Here we calculate Likelihood of Evidence and multiple all individual probabilities with priori
(Outcome|Multiple Evidence) = P(Evidence1|Outcome) x P(Evidence2|outcome) x ... x P(EvidenceN|outcome) x P(Outcome)
scaled by P(Multiple Evidence)
'''
def calculate_conditional_probabilities(self, hypothesis):
for i in self.priori:
self.cp[i] = {}
for j in hypothesis:
self.cp[i].update({ hypothesis[j]: self.get_cp(j, hypothesis[j], i)})
print "\nCalculated Conditional Probabilities: \n"
pprint.pprint(self.cp)
def classify(self):
print "Result: "
for i in self.cp:
print i, " ==> ", reduce(lambda x, y: x*y, self.cp[i].values())*self.priori[i]
if __name__ == "__main__":
c = Classifier(filename="new_dataset.csv", class_attr="Buys_Computer" )
c.calculate_priori()
c.hypothesis = {"Age":'<=30', "Income":"medium", "Student":'yes' , "Creadit_Rating":'fair'}
c.calculate_conditional_probabilities(c.hypothesis)
c.classify()
Sortie:
Priori Values: {'yes': 0.6428571428571429, 'no': 0.35714285714285715}
Calculated Conditional Probabilities:
{
'no': {
'<=30': 0.8,
'fair': 0.6,
'medium': 0.6,
'yes': 0.4
},
'yes': {
'<=30': 0.3333333333333333,
'fair': 0.7777777777777778,
'medium': 0.5555555555555556,
'yes': 0.7777777777777778
}
}
Result:
yes ==> 0.0720164609053
no ==> 0.0411428571429
J'espère que cela aidera à mieux comprendre le problème
Paix
Bayes Naïf: Naive Bayes relève de la supervision de l'apprentissage automatique qui permettait de faire des classifications d'ensembles de données. Il est utilisé pour prédire les choses en fonction de ses connaissances antérieures et des hypothèses d'indépendance.
Ils l'appellent naïf parce que ses hypothèses (il suppose que toutes les fonctionnalités de l'ensemble de données sont tout aussi importantes et indépendantes) sont vraiment optimistes et rarement vraies dans la plupart des applications du monde réel.
C'est un algorithme de classification qui prend la décision pour l'ensemble de données inconnu. Il est basé sur théorème de Bayes {[11] } qui décrivent la probabilité d'un événement basé sur ses connaissances antérieures.
Le diagramme ci-dessous montre comment fonctionne naive Bayes
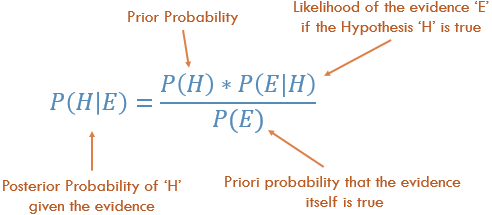
Formule pour prédire NB:
Comment utiliser L'algorithme naïf de Bayes ?
Prenons un exemple de la façon dont N. B woks
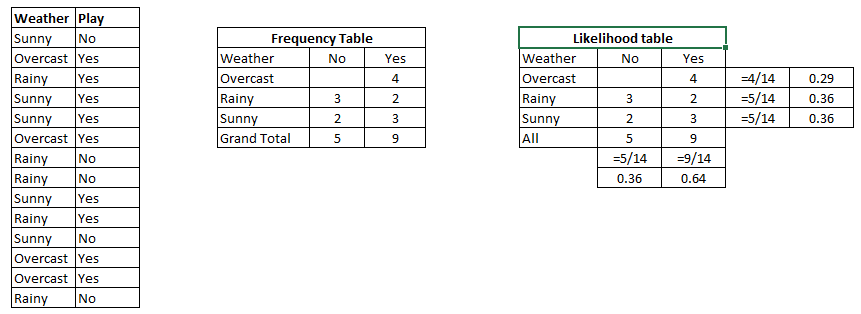
Étape 1: d'abord, nous découvrons la probabilité de tableau qui montre le Probabilité de oui ou non dans le diagramme ci-dessous. Étape 2: Trouvez la probabilité postérieure de chaque classe.
Problem: Find out the possibility of whether the player plays in Rainy condition?
P(Yes|Rainy) = P(Rainy|Yes) * P(Yes) / P(Rainy)
P(Rainy|Yes) = 2/9 = 0.222
P(Yes) = 9/14 = 0.64
P(Rainy) = 5/14 = 0.36
Now, P(Yes|Rainy) = 0.222*0.64/0.36 = 0.39 which is lower probability which means chances of the match played is low.
Pour plus de référence se référer à ces blog.
Référez-Vous Au Dépôt GitHub Naive-Bayes-Examples
J'essaie d'expliquer la règle de Bayes avec un exemple.
Supposons que vous le sachiez 10% des personnes sont des fumeurs. Vous le savez aussi 90% des fumeurs sont des hommes et 80% parmi eux ont plus de 20 ans.
Maintenant, vous voyez quelqu'un qui est un l'homme et 15 ans. Vous voulez savoir la chance qu'il est un fumeur:
X = smoker | he is a man and under 20
Puisque vous savez que 10% des personnes sont des fumeurs, votre estimation initiale est de 10% (probabilité antérieure , sans rien savoir sur la personne) mais l'autre éléments de preuve (qu'il est un homme et qu'il a 15 ans) peut affecter cette supposition.
Chaque preuve peut augmenter ou diminuer ce risque. Par exemple, ce fait qu'il est un homme Peut augmenter les chances, à condition que ce pourcentage (être un homme) parmi les non-fumeurs soit inférieur, par exemple, 40%. En d'autres termes, être un homme doit être un bon indicateur de l'être un fumeur plutôt qu'un non-fumeur.
Nous pouvons montrer cette contribution d'une autre manière. Pour chaque fonctionnalité, vous devez comparer la commonness (Probabilité) de cette fonctionnalité (f) seule avec sa commonness dans les conditions données. (P(f) vs. P(f | x). Par exemple, si nous savons que la probabilité d'être un homme est de 90% dans une société et 90% des fumeurs sont aussi des hommes, sachant que quelqu'un est un homme qui ne nous aide pas (10% * (90% / 90%) = 10%). Mais si les hommes contribuent à 40% de la société, mais 90% des fumeurs, alors de savoir que quelqu'un est un homme augmente la probabilité d'être fumeur (10% * (90% / 40%) = 22.5% ). De la même manière, si la probabilité d'être un homme a été de 95% dans la société, indépendamment du fait que le pourcentage d'hommes parmi les fumeurs est élevée (90%)! la preuve que quelqu'un est un homme diminue les chances de lui être un fumeur! (10% * (90% / 95%) = 9.5%).
Donc nous avons:
P(X) =
P(smoker)*
(P(being a man | smoker)/P(being a man))*
(P(under 20 | smoker)/ P(under 20))
Notez que dans cette formule nous avons supposé que être un homme et être sous 20 sont des caractéristiques indépendantes donc nous les avons multipliées, cela signifie que savoir que quelqu'un est sous 20 n'a aucun effet en devinant qu'il est homme ou femme. Mais ce n'est peut-être pas vrai, par exemple peut-être que la plupart des adolescents dans une société sont des hommes...
Pour utiliser cette formule dans un classificateur
Le classificateur est donné avec quelques caractéristiques (être un homme et être sous 20) et il doit décider s'il est un fumeur ou non. Il utilise la formule ci-dessus pour trouver que. Fournir les probabilités requises(90%, 10%, 80%...) il utilise l'ensemble de la formation. Par exemple, il compte les personnes dans l'ensemble de formation qui sont fumeurs et trouvent qu'ils contribuent 10% de l'échantillon. Ensuite, pour les fumeurs, vérifie combien d'entre eux sont des hommes ou des femmes .... combien sont au-dessus de 20 ou sous 20....