Pourquoi transformer les normales avec la transposée de l'inverse de la matrice modelview?
je travaille sur quelques shaders, et j'ai besoin de transformer les normaux.
j'ai lu dans quelques tutoriels de la méthode de transformation des normales est vous les multiplier avec la transposée de l'inverse de la matrice modelview. Mais je n'arrive pas à trouver d'explication sur la raison pour laquelle c'est ainsi, et quelle est la logique derrière cela?
5 réponses
jetez un coup d'oeil à ce tutoriel:
https://paroj.github.io/gltut/Illumination/Tut09%20Normal%20Transformation.html
vous pouvez imaginer que lorsque la surface d'une sphère s'étire (de sorte que la sphère est graduée le long d'un axe ou quelque chose de similaire) les normales de cette surface vont toutes "plier" vers l'un l'autre. Il s'avère que vous devez inverser l'échelle appliquée aux normales pour atteindre cet objectif. C'est la même chose que transformer avec le Inverse La Transposition De La Matrice. Le lien ci-dessus montre comment en dériver la matrice de transposition inverse.
notez aussi que lorsque l'échelle est uniforme, vous pouvez simplement passer la matrice originale comme matrice normale. Imaginez que la même sphère soit graduée uniformément le long de tous les axes, la surface ne s'étirera pas ou ne fléchira pas, pas plus que les normales.
elle découle de la définition d'une normale.
supposons que vous ayez la normale,N, et d'un vecteur, V, un vecteur tangent à la même position sur l'objet en tant que normale. Ensuite, par définition,N·V = 0.
les vecteurs Tangents exécution dans la même direction que la surface d'un objet. Donc, si votre surface est plane, alors la tangente est la différence entre deux points identifiables sur l'objet. Donc, si V = Q - R où Q et R sont des points sur le surface alors si vous transformez l'objet par B:
V' = BQ - BR
= B(Q - R)
= BV
la même logique s'applique aux surfaces non planes en considérant les limites.
dans ce cas supposez que vous avez l'intention de transformer le modèle par la matrice B. Donc B sera appliquée à la géométrie. Ensuite, pour comprendre ce qu'il faut faire pour les normales, vous devez résoudre pour la matrice, A donc:
(AN)·(BV) = 0
transformer cela en une ligne versus colonne chose pour éliminer l'explicite produit scalaire:
[tranpose(AN)](BV) = 0
Tirez le transposer à l'extérieur, d'éliminer les parenthèses:
transpose(N)*transpose(A)*B*V = 0
donc c'est "la transposition de la normale" [produit avec] "la transposition de la matrice de transformation connue" [produit avec] "la transformation que nous résolvons pour" [produit avec] "le vecteur à la surface du modèle" = 0
Mais nous avons commencé par affirmer que transpose(N)*V = 0 vu que c'est la même chose que de dire que N·V = 0. Donc, pour satisfaire nos contraintes, nous avons besoin de partie centrale de l'expression - transpose(A)*B - pour aller loin.
on peut donc conclure que:
transpose(A)*B = identity
=> transpose(A) = identity*inverse(B)
=> transpose(A) = inverse(B)
=> A = transpose(inverse(B))
ma preuve préférée est en dessous où N est la normale et V est un vecteur tangent. Puisqu'ils sont perpendiculaires leur produit de point est zéro. M est toute transformation inversible de 3x3 (M -1 * M = I). N 'et V' sont les vecteurs transformés par M.
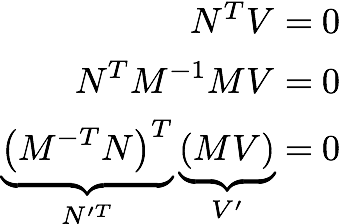
pour obtenir un peu d'intuition, considérez la transformation de cisaillement ci-dessous.
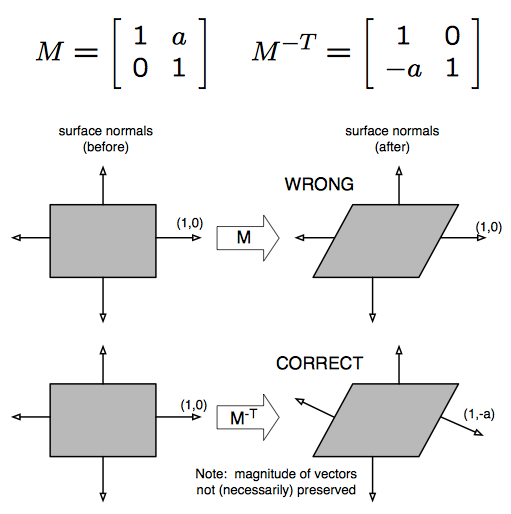
notez que cela fait appliquer aux vecteurs tangents.
si la matrice du modèle est faite de translation, rotation et échelle, vous n'avez pas besoin de faire une transposition inverse pour calculer la matrice normale. Il suffit de diviser la normale par l'échelle au carré et de multiplier par matrice de modèle et nous sommes faits. Vous pouvez étendre cela à n'importe quelle matrice avec des axes perpendiculaires, il suffit de calculer l'échelle carrée pour chaque axe de la matrice que vous utilisez à la place.
j'ai écrit les détails dans mon blog: https://lxjk.github.io/2017/10/01/Stop-Using-Normal-Matrix.html
Je ne comprends pas pourquoi vous ne mettez pas à zéro le 4ème élément du vecteur de direction avant de le multiplier avec la matrice du modèle. Pas besoin d'inverser ou de transposer. Pensez au vecteur de direction comme la différence entre deux points. Déplacer les deux points avec le reste du modèle - ils sont toujours dans la même position relative au modèle. La différence entre les deux points pour obtenir la nouvelle direction, et le 4ème élément, annule à zéro. Beaucoup moins cher.