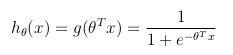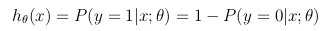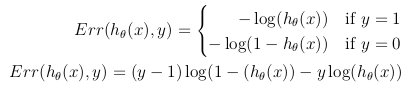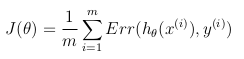Pourquoi le coût de la fonction de régression logistique a une expression logarithmique?
fonction de coût pour la régression logistique est
cost(h(theta)X,Y) = -log(h(theta)X) or -log(1-h(theta)X)
ma question Est de savoir quelle est la base de l'expression logarithmique pour la fonction de coût .D'où vient-elle? je crois que tu ne peux pas sortir "-log" de nulle part. Si quelqu'un pouvait expliquer la dérivation de la fonction de coût, je vous serais reconnaissant. remercier.
3 réponses
Source: mes propres notes prises pendant Standford Machine du cours d'Apprentissage en Coursera, par Andrew Ng. Tous les remerciements à lui et à cette organisation. Le cours est disponible gratuitement pour quiconque d'être pris à leur propre rythme. Les images sont faites par moi-même en utilisant LaTeX (formules) et R (graphiques).
fonction D'hypothèse
régression Logistique est utilisée lorsque la variable o c'est voulu être prédit peut seulement prendre des valeurs discrètes (c.-à-d.: classification).
Considérant un problème de classification binaire (o ne peut prendre que deux valeurs), puis d'avoir un ensemble de paramètres θ et un ensemble d'entités en entrée x, la fonction d'hypothèse pourrait être définie de façon à être limitée entre [0, 1], dans laquelle g () représente la fonction sigmoïde:
cette fonction d'hypothèse représente en même temps la probabilité estimée que y = 1 entrée x paramétrée par θ:
fonction de Coût
la fonction de coût représente l'objectif d'optimisation.
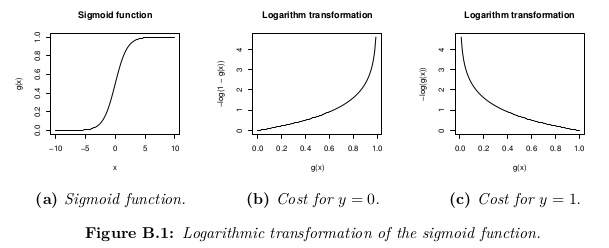
Bien qu'une définition possible de la fonction de coût pourrait être la moyenne de la distance Euclidienne entre l'hypothèse h_θ (x) et la valeur réelle o parmi tous les m des échantillons dans l'ensemble de la formation, aussi longtemps que l'hypothèse d'une fonction est constituée avec la fonction sigmoïde, cette définition se traduirait par une fonction de coût non convexe, ce qui signifie qu'il est facile de trouver un minimum local avant d'atteindre le minimum global. Afin de s'assurer que la fonction de coût est convexe (et donc assurer la convergence au minimum global), la fonction de coût est transformé en utilisant le logarithme de la fonction sigmoïde.
de cette façon la fonction d'objectif d'optimisation peut être définie comme la moyenne des coûts/erreurs dans l'ensemble de formation:
cette fonction de coût est simplement une reformulation du critère de vraisemblance maximale(log).
le modèle de régression logistique est:
P(y=1 | x) = logistic(θ x)
P(y=0 | x) = 1 - P(y=1 | x) = 1 - logistic(θ x)
La probabilité s'écrit:
L = P(y_0, ..., y_n | x_0, ..., x_n) = \prod_i P(y_i | x_i)
La log-vraisemblance est:
l = log L = \sum_i log P(y_i | x_i)
Nous voulons trouver θ qui maximise la probabilité:
max_θ \prod_i P(y_i | x_i)
C'est la même que la maximisation de la log-vraisemblance:
max_θ \sum_i log P(y_i | x_i)
Nous pouvons réécrire cette comme une minimisation du coût C= - l:
min_θ \sum_i - log P(y_i | x_i)
P(y_i | x_i) = logistic(θ x_i) when y_i = 1
P(y_i | x_i) = 1 - logistic(θ x_i) when y_i = 0
ma compréhension (pas 100% expert ici, je peux me tromper) est que le log peut s'expliquer en gros comme dés-faire le exp qui apparaît dans la formule gaussien densité de probabilité. (Rappelez-vous -log(x) = log(1/x).)
si je comprends bien Bishop [1] correctement: quand nous supposons que nos échantillons d'entraînement positifs et négatifs proviennent de deux clusters gaussiens différents (emplacement différent mais même covariance) alors nous pouvons développer un classificateur parfait. Et ce le classificateur ressemble à la régression logistique (par exemple, limite de décision linéaire).
bien sûr, la question suivante est pourquoi devrions-nous utiliser un classificateur qui est optimal pour séparer les clusters gaussiens, alors que nos données de formation semblent souvent différentes?
[1] reconnaissance de motifs et apprentissage automatique, Christopher M. Bishop, chapitre 4.2 (modèles génératifs probabilistes)