Quelle est la différence entre la régression linéaire et la régression logistique?
Lorsque nous avons à prédire la valeur d'un catégorique (ou discrètes) résultat nous utilisons régression logistique. Je crois que nous utilisons régression linéaire pour prédire également la valeur d'un résultat compte tenu des valeurs d'entrée.
Alors, quelle est la différence entre les deux méthodes?
11 réponses
-
Sortie de régression linéaire comme probabilités
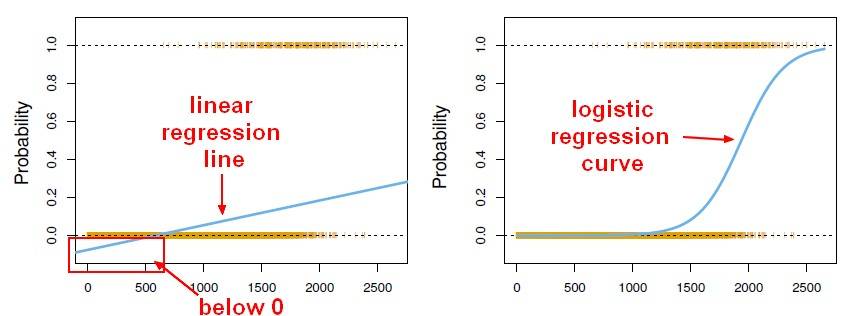
Il est tentant d'utiliser la sortie de régression linéaire comme probabilités mais c'est une erreur car la sortie peut être négative, et supérieure à 1 alors que la probabilité ne peut pas. Comme la régression pourrait réellement produire des probabilités qui pourraient être inférieures à 0, ou même plus grandes que 1, la régression logistique a été introduite.
Source: http://gerardnico.com/wiki/data_mining/simple_logistic_regression
-
Résultat
En régression linéaire, le résultat (variable dépendante) est continu. Il peut avoir n'importe laquelle d'un nombre infini de valeurs possibles.
Dans la régression logistique, le résultat (variable dépendante) n'a qu'un nombre limité de valeurs possibles.
-
La variable dépendante
La régression logistique est utilisé lorsque la variable de réponse est de nature catégorique. Par exemple, oui/non, vrai/faux, rouge/vert/bleu, 1ère/2ème/3ème/4ème, etc.
La régression linéaire est utilisée lorsque votre variable de réponse est continue. Par exemple, le poids, la hauteur, le nombre d'heures, etc.
-
L'Équation
La régression linéaire donne une équation de la forme Y = mX + C, moyens équation de degré 1.
Cependant, la régression logistique donne une équation qui est de la forme Y = eX + e X
-
Interprétation du Coefficient
En régression linéaire, l'interprétation des coefficients des variables indépendantes est assez simple (c.-à-D. en maintenant toutes les autres variables constantes, avec une augmentation unitaire de cette variable, la variable dépendante devrait augmenter/diminuer de xxx).
Cependant, en régression logistique, dépend de la famille (binôme, Poisson, etc.) et lien (log, logit, inverse-log, etc.) vous l'utilisation, l'interprétation est différente.
-
Technique de minimisation des erreurs
La régression linéaire utilise la méthode des moindres carrés ordinaires pour erreurs et arriver à un meilleur ajustement possible, tandis que la régression logistique utilise la méthodemaximum de vraisemblance pour arriver à la solution.
La régression linéaire est généralement résolue en minimisant l'erreur des moindres carrés du modèle aux données, donc les erreurs importantes sont pénalisées quadratiquement.
La régression logistique est tout le contraire. L'utilisation de la fonction de perte logistique entraîne la pénalisation des erreurs importantes à une constante asymptotiquement.
Considérez la régression linéaire sur les résultats catégoriques {0, 1} pour voir pourquoi c'est un problème. Si votre modèle prédit que le résultat est 38, lorsque la vérité est 1, vous n'avez rien perdu. La régression linéaire essaierait de réduire ce 38, la logistique ne le ferait pas (autant)2.
En régression linéaire, le résultat (variable dépendante) est continu. Il peut avoir n'importe laquelle d'un nombre infini de valeurs possibles. Dans la régression logistique, le résultat (variable dépendante) n'a qu'un nombre limité de valeurs possibles.
Par exemple, si X contient la superficie en pieds carrés des maisons et Y contient le prix de vente correspondant de ces maisons, vous pouvez utiliser une régression linéaire pour prédire le prix de vente en fonction de la taille de la maison. Alors que le prix de vente possible peut ne pas être en fait any , Il y a tellement de valeurs possibles qu'un modèle de régression linéaire serait choisi.
Si, au lieu de cela, vous vouliez prédire, en fonction de la taille, si une maison se vendrait pour plus de 200 000$, vous utiliseriez la régression logistique. Les sorties possibles sont soit oui, la maison se vendra pour plus de 200K$, ou non, la maison ne sera pas.
En termes simples, la régression linéaire est un algorithme de régression, qui génère une valeur continue et infinie possible; la régression logistique est considérée comme un algorithme de classificateur binaire, qui génère la "probabilité" de l'entrée appartenant à une étiquette (0 ou 1).
La différence de base :
La régression linéaire est fondamentalement un modèle de régression qui signifie qu'elle donnera une sortie non discrète / continue d'une fonction. Donc, cette approche donne de la valeur. Par exemple: donné x ce qui est f (x)
Par exemple, étant donné un ensemble de formation de différents facteurs et le prix d'une propriété après la formation, nous pouvons fournir les facteurs nécessaires pour déterminer quel sera le prix de la propriété.
La régression logistique est fondamentalement une classification binaire algorithme qui signifie qu'ici il y aura une sortie discrète pour la fonction . Par exemple: pour un X donné si F(x)>seuil classifiez-le à 1 sinon classifiez-le à 0.
Par exemple, étant donné un ensemble de taille de tumeur cérébrale comme données d'entraînement, nous pouvons utiliser la taille comme entrée pour déterminer s'il s'agit d'une tumeur bénigne ou maligne. Donc ici la sortie est discrète soit 0 soit 1.
* ici, la fonction est fondamentalement la fonction d'hypothèse
Ils sont tous deux assez similaires dans la résolution de la solution, mais comme d'autres l'ont dit, l'un (régression logistique) est pour prédire une catégorie "fit" (Y/N ou 1/0), et l'autre (régression linéaire) est pour prédire une valeur.
Donc, si vous voulez prédire si vous avez un cancer Y/N (ou une probabilité) - utilisez logistic. Si vous voulez savoir combien d'années vous allez vivre à utiliser la Régression Linéaire !
Juste pour ajouter les réponses précédentes.
La régression Linéaire
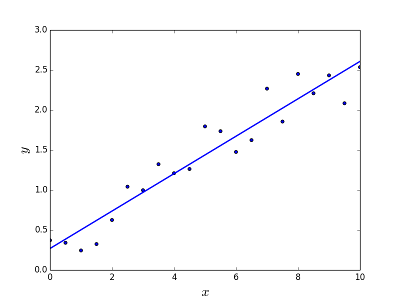
Est destiné à résoudre le problème de la prédiction / estimation de la valeur de sortie pour un élément X donné (disons f (x)). Le résultat de la prédiction est une fonction cotinueuse où les valeurs peuvent être positives ou négatives. Dans ce cas, vous avez normalement un jeu de données d'entrée avec beaucoup de exemples et la valeur de sortie pour chacun d'eux. L'objectif est de pouvoir adapter un modèle à cet ensemble de données vous êtes donc en mesure de prédire cette sortie pour de nouveaux éléments différents/jamais vus. Voici l'exemple classique d'ajustement d'une ligne à un ensemble de points, mais en général la régression linéaire pourrait être utilisée pour adapter des modèles plus complexes (en utilisant des degrés polynomiaux plus élevés):
La régression Linea peut être résolue de deux manières différentes:
- équation normale (moyen direct de résoudre le problème)
- descente de Gradient (itérative approche)
Régression Logistique
Est destiné à résoudre les problèmes de classification où, étant donné un élément, vous devez classer le même dans N catégories. Des exemples typiques sont par exemple donnés un courrier pour le classer comme spam ou non, ou donné un véhicule trouver à quelle catégorie il appartient (voiture, camion, van, etc..). C'est essentiellement la sortie est un ensemble fini de valeurs descrete.
Résoudre le problème
Régression logistique les problèmes ne pouvaient être résolus qu'en utilisant la descente en pente. La formulation en général est très similaire à la régression linéaire la seule différence est l'utilisation de la fonction d'hypothèse différente. En régression linéaire, l'hypothèse a la forme:
h(x) = theta_0 + theta_1*x_1 + theta_2*x_2 ..
Où theta est le modèle que nous essayons d'adapter et de [1, x_1, x_2, ..] est le vecteur d'entrée. Dans la régression logistique, la fonction d'hypothèse est différente:
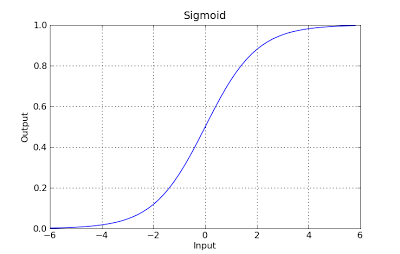
g(x) = 1 / (1 + e^-x)
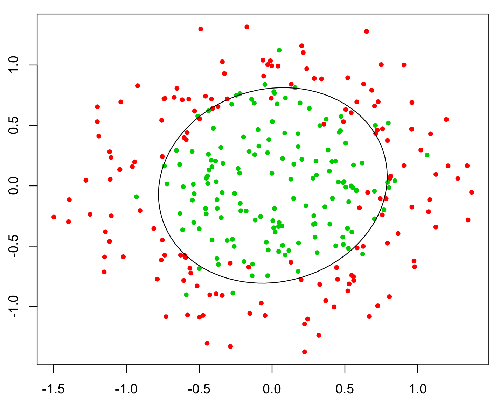
Cette fonction a une belle propriété, fondamentalement, il mappe toute valeur à la plage [0,1] qui est appropriée pour gérer les propababilités pendant la classificatine. Par exemple dans le cas d'une classification binaire g(X) peut être interprété comme la probabilité d'appartenir à la classe. Dans ce cas, normalement, vous avez différentes classes qui sont séparées par une limite de décision qui fondamentalement une courbe qui décide de la séparation entre les différentes classes. Voici un exemple d'ensemble de données séparé en deux classe.
En bref: La régression linéaire donne une sortie continue. c'est à dire une valeur entre une plage de valeurs. La régression logistique donne une sortie discrète. c'est-à-dire oui / non, 0/1 type de sorties.
| Basis | Linear | Logistic |
|-----------------------------------------------------------------|--------------------------------------------------------------------------------|---------------------------------------------------------------------------------------------------------------------|
| Basic | The data is modelled using a straight line. | The probability of some obtained event is represented as a linear function of a combination of predictor variables. |
| Linear relationship between dependent and independent variables | Is required | Not required |
| The independent variable | Could be correlated with each other. (Specially in multiple linear regression) | Should not be correlated with each other (no multicollinearity exist). |
Ne peut être plus d'accord avec les commentaires ci-dessus. Au-dessus de cela, il y a quelques autres différences comme
Dans la régression linéaire, on suppose que les résidus sont normalement distribués. Dans la régression logistique, les résidus doivent être indépendants mais pas normalement distribués.
Régression Linéaire suppose qu'un changement constant de la valeur de la variable explicative des résultats en constante évolution dans la variable de réponse. Cette hypothèse ne tient pas si la valeur de la variable de réponse représente une probabilité (en Régression Logistique)
GLM (Generalized linear models) ne suppose pas une relation linéaire entre les variables dépendantes et indépendantes. Cependant, il suppose une relation linéaire entre la fonction de lien et les variables indépendantes dans le modèle logit.
Pour le dire simplement, si dans le modèle de régression linéaire plus de cas de test arrivent qui sont loin du seuil (disons =0.5) pour une prédiction de y = 1 et y = 0. Ensuite, dans ce cas, l'hypothèse va changer et s'aggraver.Donc modèle de régression linéaire n'est pas utilisé pour la classification problème.
Un autre problème est que si la classification est y=0 et y=1, h (x) peut être > 1 ou
La régression logistique est utilisée pour prédire les sorties catégoriques comme Oui / Non, Faible / Moyen / Élevé, etc. Vous avez essentiellement 2 types de régression logistique régression logistique binaire (oui / non, approuvé/ désapprouvé) ou régression logistique multi-classes (Faible/Moyen/Élevé, chiffres de 0-9 etc)
D'autre part, la régression linéaire est si votre variable dépendante (y) est continue. y = mx + c est une équation de régression linéaire simple (M = pente et c est l'ordonnée à l'origine). La régression multilinéaire a plus de 1 variable indépendante (x1, x2, x3 ... etc)