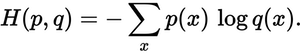Qu'est-ce que logits, softmax et softmax cross entropy avec logits?

Version Courte:

Supposons que vous ayez deux tenseurs, où y_hat contient des scores calculés pour chaque classe (par exemple, à partir de y = W * x + b)et y_true contient des étiquettes vraies codées à chaud.

y_hat  = ... # Predicted label, e.g. y = tf.matmul(X, W) + b
y_true = ... # True label, one-hot encoded

Si vous interprétez les scores dans y_hat comme des probabilités logiques non normalisées, alors ils sont logits .

De plus, la perte totale d'entropie croisée calculée de cette manière:

y_hat_softmax = tf.nn.softmax(y_hat)
total_loss = tf.reduce_mean(-tf.reduce_sum(y_true * tf.log(y_hat_softmax), [1]))

Est essentiellement équivalent à la perte totale d'entropie croisée calculé avec la fonction softmax_cross_entropy_with_logits():

total_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_hat, y_true))

Version Longue:

Dans la couche de sortie de votre réseau neuronal, vous calculerez probablement un tableau contenant les scores de classe pour chacune de vos instances d'entraînement, par exemple à partir d'un calcul y_hat = W*x + b. Pour servir d'exemple, ci-dessous, j'ai créé un y_hat en tant que Tableau 2 x 3, où les lignes correspondent aux instances d'apprentissage et les colonnes correspondent aux classes. Donc ici il y a 2 instances de formation et 3 classe.

import tensorflow as tf
import numpy as np

sess = tf.Session()

# Create example y_hat.
y_hat = tf.convert_to_tensor(np.array([[0.5, 1.5, 0.1],[2.2, 1.3, 1.7]]))
sess.run(y_hat)
# array([[ 0.5,  1.5,  0.1],
#        [ 2.2,  1.3,  1.7]])

Notez que les valeurs ne sont pas normalisées (c'est-à-dire que les lignes ne s'additionnent pas à 1). Afin de les normaliser, nous pouvons appliquer la fonction softmax, qui interprète l'entrée comme des probabilités logiques non normalisées (aka logits) et génère des probabilités linéaires normalisées.

y_hat_softmax = tf.nn.softmax(y_hat)
sess.run(y_hat_softmax)
# array([[ 0.227863  ,  0.61939586,  0.15274114],
#        [ 0.49674623,  0.20196195,  0.30129182]])

Il est important de bien comprendre ce que dit la sortie softmax. Ci-dessous, j'ai montré un tableau qui représente plus clairement la sortie ci-dessus. Il peut être vu que, par exemple, l' la probabilité que l'instance d'entraînement 1 soit "Classe 2" est de 0,619. Les probabilités de classe pour chaque instance d'apprentissage sont normalisées, de sorte que la somme de chaque ligne est 1.0.

                      Pr(Class 1)  Pr(Class 2)  Pr(Class 3)
                    ,--------------------------------------
Training instance 1 | 0.227863   | 0.61939586 | 0.15274114
Training instance 2 | 0.49674623 | 0.20196195 | 0.30129182

Nous avons donc maintenant des probabilités de classe pour chaque instance d'apprentissage, où nous pouvons prendre l'argmax () de chaque ligne pour générer une classification finale. D'en haut, nous pouvons générer que l'instance de formation 1 appartient à "classe 2" et que l'instance de formation 2 appartient à "classe 1".

Ces classifications sont-elles correctes? Nous avons besoin de pour mesurer par rapport aux vraies étiquettes de l'ensemble de formation. Vous aurez besoin d'un tableau y_true encodé à chaud, où encore une fois les lignes sont des instances d'apprentissage et les colonnes sont des classes. Ci-dessous, j'ai créé un exemple y_true Un tableau à chaud où l'étiquette vraie pour l'instance de formation 1 est "Classe 2" et l'étiquette vraie pour l'instance de formation 2 est "Classe 3".

y_true = tf.convert_to_tensor(np.array([[0.0, 1.0, 0.0],[0.0, 0.0, 1.0]]))
sess.run(y_true)
# array([[ 0.,  1.,  0.],
#        [ 0.,  0.,  1.]])

Est la distribution de probabilité dans y_hat_softmax proche de la distribution de probabilité dans y_true? Nous pouvons utiliser entropie croisée pour mesure de l'erreur.

Nous pouvons calculer la perte d'entropie croisée sur une base linéaire et voir les résultats. Ci-dessous, nous pouvons voir que l'instance d'entraînement 1 a une perte de 0.479, tandis que l'instance d'entraînement 2 a une perte plus élevée de 1.200. Ce résultat est logique car dans notre exemple ci-dessus, y_hat_softmax a montré que la probabilité la plus élevée de l'instance d'entraînement 1 était pour la "classe 2", qui correspond à l'instance d'entraînement 1 dans y_true; cependant, la prédiction pour l'instance d'entraînement 2 a montré un Probabilité la plus élevée pour "Classe 1", qui ne correspond pas à la vraie classe "Classe 3".

loss_per_instance_1 = -tf.reduce_sum(y_true * tf.log(y_hat_softmax), reduction_indices=[1])
sess.run(loss_per_instance_1)
# array([ 0.4790107 ,  1.19967598])

Ce que nous voulons vraiment, c'est la perte totale sur toutes les instances d'entraînement. Nous pouvons donc calculer:

total_loss_1 = tf.reduce_mean(-tf.reduce_sum(y_true * tf.log(y_hat_softmax), reduction_indices=[1]))
sess.run(total_loss_1)
# 0.83934333897877944

Utilisation de softmax_cross_entropy_with_logits()

Nous pouvons plutôt calculer la perte totale d'entropie croisée en utilisant la fonction tf.nn.softmax_cross_entropy_with_logits(), comme indiqué ci-dessous.

loss_per_instance_2 = tf.nn.softmax_cross_entropy_with_logits(y_hat, y_true)
sess.run(loss_per_instance_2)
# array([ 0.4790107 ,  1.19967598])

total_loss_2 = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_hat, y_true))
sess.run(total_loss_2)
# 0.83934333897877922

Notez que total_loss_1 et total_loss_2 produisent des résultats essentiellement équivalents avec quelques petites différences dans le très derniers chiffres. Cependant, vous pouvez aussi bien utiliser la deuxième approche: il faut une ligne de code de moins et accumule moins d'erreurs numériques car le softmax est fait pour vous à l'intérieur de softmax_cross_entropy_with_logits().

tf.nn.softmax calcule la propagation vers l'avant à travers une couche softmax. Vous l'utilisez pendant évaluation du modèle lorsque vous calculez les probabilités que les sorties du modèle.

tf.nn.softmax_cross_entropy_with_logits calcule le coût d'un softmax couche. Il n'est utilisé que pendant la formation .

Les logits sont les probabilités de log unnormalized sortie du modèle (les valeurs de sortie avant la normalisation softmax leur est appliquée).

Les réponses ci-dessus ont suffisamment de description pour la question posée.

En plus de cela, Tensorflow a optimisé l'opération d'application de la fonction d'activation puis de calcul du coût en utilisant sa propre activation suivie de fonctions de coût. C'est donc une bonne pratique d'utiliser: tf.nn.softmax_cross_entropy() over tf.nn.softmax(); tf.nn.cross_entropy()

Vous pouvez trouver une différence importante entre eux dans un modèle gourmand en ressources.

Logit est une fonction qui mappe les probabilités [0, 1] à [- inf, + inf]. Tensorflow "avec logit": cela signifie que vous appliquez une fonction softmax aux nombres logit pour les normaliser. Le input_vector / logit n'est pas normalisé et peut évoluer à partir de [- inf, inf].

Cette normalisation est utilisée pour les problèmes de classification multiclasse. Et pour les problèmes de classification multilabel, la normalisation sigmoïde est utilisée, c'est-à-dire tf.nn.sigmoid_cross_entropy_with_logits