Comprendre La Rétropagation Des Réseaux Neuronaux
mise à Jour: une meilleure formulation de la question.
j'essaie de comprendre l'algorithme de rétropropagation avec un réseau neuronal XOR comme exemple. Dans ce cas, il y a 2 neurones d'entrée + 1 biais, 2 neurones dans la couche cachée + 1 biais et 1 neurone de sortie.
A B A XOR B
1 1 -1
1 -1 1
-1 1 1
-1 -1 -1

j'utilise stochastique les.
Après avoir lu un peu plus j'ai trouvé que l'erreur de l'unité de production est de propagée aux couches cachées... au début, c'était confus, parce que quand vous arrivez à la couche d'entrée du réseau neuronal, alors chaque neurone obtient un ajustement d'erreur des deux neurones dans la couche cachée. En particulier, la façon dont l'erreur est répartie est difficile à saisir au début.
Etape 1 calculer la sortie pour chaque instance de l'entrée.
Etape 2 calculer l'erreur entre le(s) neurone (s) de sortie (dans notre cas là est un seul) et la valeur cible(s):
Étape 2 http://pandamatak.com/people/anand/771/html/img342.gif
Étape 3 nous utilisons l'erreur à partir de l'Étape 2 pour calculer l'erreur pour chaque unité cachées h:
Étape 3 http://pandamatak.com/people/anand/771/html/img343.gif
le 'poids kh' est le poids entre l'unité cachée h et l'Unité de sortie k, bien c'est déroutant parce que l'unité d'entrée ne pas directement de poids associé à l'unité de sortie. Après avoir regardé la formule pendant quelques heures, j'ai commencé à réfléchir à ce que signifie la sommation, et je commence à en arriver à la conclusion que le poids de chaque neurone d'entrée qui se connecte aux neurones de la couche cachée est multiplié par l'erreur de sortie et résumé. C'est une conclusion logique, mais la formule semble un peu confuse car elle dit clairement le "poids kh" (entre la couche de sortie k et la couche cachée) h.)
est-ce que je comprends tout correctement ici? Quelqu'un peut-il confirmer cela?
Qu'est-ce que O( h) de la couche d'entrée? Ma compréhension est que chaque nœud d'entrée a deux sorties: l'une qui va dans le le premier nœud de la couche cachée et qui va dans le deuxième nœud couche cachée. Laquelle des deux sorties doit être branchée dans le O(h)*(1 - O(h)) partie de la formule?
Étape 3 http://pandamatak.com/people/anand/771/html/img343.gif
3 réponses
le tutoriel que vous avez posté ici est en fait en train de le faire mal. J'ai vérifié contre l'Évêque de deux livres et deux de mes implémentations de travail. Je vous indiquerai ci-dessous où exactement.
une chose importante à garder à l'esprit est que vous êtes toujours à la recherche de dérivés de la fonction d'erreur en ce qui concerne une unité ou un poids. Les premiers sont les deltas, les derniers sont ceux que vous utilisez pour mettre à jour vos poids.
Si vous voulez comprendre les, vous comprendre la chaîne de la règle. Il s'agit de la règle de la chaîne. Si vous ne savez pas comment cela fonctionne exactement, vérifier sur wikipedia, il n'est pas difficile. Mais dès que vous comprenez les dérivations, tout tombe en place. La promesse! :)
∂E/∂W peut être composé en ∂E/∂o ∂o / ∂W via la règle de la chaîne. ∂O / ∂W est facile à calculer, puisqu'il s'agit simplement de la dérivée de l'activation/sortie d'une unité par rapport aux poids. ∂E / ∂o est en fait ce que nous appelons les deltas. (Je suis en supposant que E, o et W sont des vecteurs / matrices ici)
Nous avons pour les unités de sortie, puisque c'est là que nous pouvons calculer l'erreur. (La plupart du temps, nous avons une fonction d'erreur qui descend à delta de (t_k - o_k), par exemple pour la fonction d'erreur quadratique dans le cas de sorties linéaires et entropie croisée dans le cas de sorties logistiques.)
la question est maintenant, comment obtenir les dérivés pour les unités internes? Eh bien, nous savons que la sortie d'une unité est la somme de toutes les unités entrantes pondérées par leur poids et l'application ultérieure d'une fonction de transfert. Donc o_k = f(sum(w_kj * o_j, pour tous les j)).
donc ce que nous faisons est, dériver o_k par rapport à o_j. Puisque delta_j = ∂E/∂o_j = ∂E/∂o_k ∂o_k/∂o_j = delta_k ∂o_k / o_j. Donc avec delta_k, on peut calculer delta_j!
faisons cela. o_k = f(sum(w_kj * o_j, pour tous les j)) => ∂o_k/∂o_j = f'(somme(w_kj * o_j, pour tous les j)) * w_kj = f'(z_k) * w_kj.
pour le cas du sigmoidal fonction de transfert, qui devient z_k (1-z_k) * w_kj. (Voici l'erreur dans le tutoriel, l'auteur dit o_k(1 - o_k) * w_kj!)
Je ne suis pas sûr de ce qu'est votre question, mais j'ai moi-même passé par ce tutoriel et je peux vous assurer, à part une faute de frappe évidente, qu'il n'y a rien d'incorrect à ce sujet.
je vais faire l'hypothèse que votre question est parce que vous êtes confus sur la façon dont la rétropagation cachée delta est dérivé. Si c'est bien votre question alors s'il vous plaît considérer
texte alternatif http://pandamatak.com/people/anand/771/html/img334.gif
Vous êtes probablement confus quant à la façon dont l'auteur dérivée de cette équation. Il s'agit en fait d'une application simple de la règle de la chaîne multivariée. À savoir, (ce qui suit est tiré de wikipédia)
" supposons que chaque argument de z = f(u, v) est une fonction à deux variables telle que u = h(x, y) et v = g (x, y), et que ces fonctions sont toutes différentiables. Alors la règle de la chaîne aurait l'air comme:
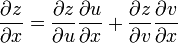
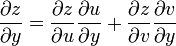 "
"
maintenant, imaginez étendre la règle de chaîne par un argument d'induction à
E (z' 1, z' 2,..,z' n) où z' k est la sortie de la couche de sortie kth pré-activation, et z' k(w ji) c'est-à-dire que E est une fonction de z' et z " est une fonction de w ji (si ce n'est pas faire sens pour vous, au début penser très soigneusement sur la façon dont un nn est configuré.) Appliquant la règle de chaîne directement étendue à n variables:
∆ e(z' 1, z' 2,..,z' n)/ δw ji = Σ k ∆ e/ δz' k δz' k/ δw ji
qui est le plus étape importante, l'auteur applique alors à nouveau la règle de la chaîne, cette fois dans la somme pour étendre le δz' k/ δw ji terme, c'est -
δz' k/ δw ji = δz' k/ δo j δo j/ δz j δz j/ δw ji.
si vous avez des difficultés à comprendre la règle de la chaîne, vous pourriez avoir besoin de suivre un cours sur le calcul multivarié, ou lire une telle section dans un manuel.
Bonne chance.
ce que j'ai lu de l'équation de L'Étape 3 est:
- O_h = dernière sortie de cette unité cachées (O_h sur la couche d'entrée est la réelle valeur d'entrée)
- w_kh = poids de la connexion entre l'unité cachées et d'une unité de la couche suivante (vers la sortie)
- delta_k = erreur de l'Unité de la couche suivante (vers la sortie, même unité que la puce précédente)
Chaque unité dispose d'une seule sortie, mais chaque lien entre la production et la couche suivante est pondéré. Donc la sortie est la même, mais du côté de la réception, chaque unité recevra une valeur différente si le poids des liens est différent. O_h se réfère toujours à la valeur de ce neurone pour la dernière itération. D'erreur ne s'applique pas à la couche d'entrée, car, par définition, l'entrée n'a pas de "erreur" en soi.
l'erreur doit être calculée couche par couche, en commençant par la sortie, car nous avons besoin des valeurs d'erreur de la couche N+1 pour calculer la couche N. Vous avez raison, il n'y a pas connexion directe entre l'entrée et la sortie dans les.
je crois que l'équation est correcte, si contraire à l'intuition. Ce qui est probablement déroutant est que dans la propagation vers l'avant pour chaque unité nous devons considérer toutes les unités et les liens à gauche de l'unité (valeurs d'entrée), mais pour la propagation d'erreur (rétroprojection) a dû considérer les unités à droite (valeur de sortie) de l'unité en cours de traitement.