Reconnaissance des formes dans les séries chronologiques]
en traitant un graphique de séries chronologiques, je voudrais détecter des modèles qui ressemblent à ceci:

à l'aide d'un exemple de série temporelle, je voudrais être capable de détecter les modèles marqués ici:
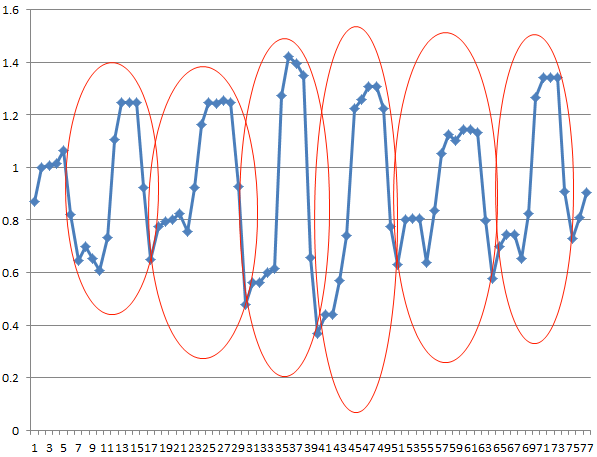
quel type d'algorithme AI (je suppose des techniques d'apprentissage de marchine) dois-je utiliser pour atteindre cet objectif? Est-il bibliothèque (en C/C++) que je peux utiliser?
5 réponses
voici un exemple de résultat d'un petit projet que j'ai fait pour la partition des données ecg.
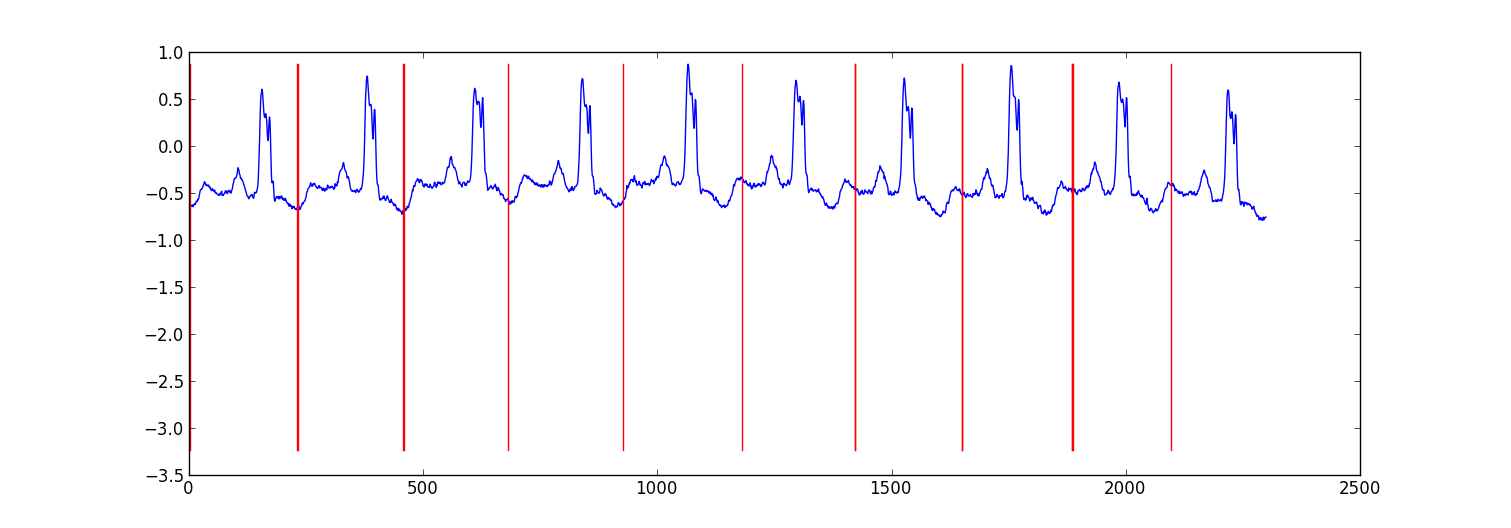
mon approche était une "commutation autorégressive HMM" (google si vous n'en avez pas entendu parler) où chaque point de données est prédite à partir du point de données précédent en utilisant un modèle de régression Bayésienne. J'ai créé 81 États cachés: un État junk pour capturer des données entre chaque battement, et 80 États cachés distincts correspondant à des positions différentes. dans le battement de coeur modèle. Les États du pattern 80 ont été construits directement à partir d'un pattern de battement simple sous - échantillonné et ont eu deux transitions-une auto-transition et une transition à l'état suivant du pattern. L'état final dans le modèle est passé à lui-même ou à l'état junk.
j'ai formé le modèle avec formation Viterbi , mettant à jour seulement les paramètres de régression.
Les résultats du testétaient adéquats dans la plupart des cas. Un de la même façon, le champ aléatoire conditionnel de structure serait probablement plus performant, mais la formation d'un CRF nécessiterait des modèles d'étiquetage manuel dans l'ensemble de données si vous n'avez pas déjà des données étiquetées.
Edit:
Voici un exemple de code python - il n'est pas parfait, mais il donne l'approche générale. Il met en œuvre EM plutôt que Viterbi formation, qui peut être un peu plus stable. L'ensemble de données ecg est de http://www.cs.ucr.edu/~eamonn/discords/ECG_data.zip
import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt
import scipy.linalg as lin
import re
data=np.array(map(lambda l: map(float,filter(lambda x: len(x)>0,re.split('\s+',l))),open('chfdb_chf01_275.txt'))).T
dK=230
pattern=data[1,:dK]
data=data[1,dK:]
def create_mats(dat):
'''
create
A - an initial transition matrix
pA - pseudocounts for A
w - emission distribution regression weights
K - number of hidden states
'''
step=5 #adjust this to change the granularity of the pattern
eps=.1
dat=dat[::step]
K=len(dat)+1
A=np.zeros( (K,K) )
A[0,1]=1.
pA=np.zeros( (K,K) )
pA[0,1]=1.
for i in xrange(1,K-1):
A[i,i]=(step-1.+eps)/(step+2*eps)
A[i,i+1]=(1.+eps)/(step+2*eps)
pA[i,i]=1.
pA[i,i+1]=1.
A[-1,-1]=(step-1.+eps)/(step+2*eps)
A[-1,1]=(1.+eps)/(step+2*eps)
pA[-1,-1]=1.
pA[-1,1]=1.
w=np.ones( (K,2) , dtype=np.float)
w[0,1]=dat[0]
w[1:-1,1]=(dat[:-1]-dat[1:])/step
w[-1,1]=(dat[0]-dat[-1])/step
return A,pA,w,K
#initialize stuff
A,pA,w,K=create_mats(pattern)
eta=10. #precision parameter for the autoregressive portion of the model
lam=.1 #precision parameter for the weights prior
N=1 #number of sequences
M=2 #number of dimensions - the second variable is for the bias term
T=len(data) #length of sequences
x=np.ones( (T+1,M) ) # sequence data (just one sequence)
x[0,1]=1
x[1:,0]=data
#emissions
e=np.zeros( (T,K) )
#residuals
v=np.zeros( (T,K) )
#store the forward and backward recurrences
f=np.zeros( (T+1,K) )
fls=np.zeros( (T+1) )
f[0,0]=1
b=np.zeros( (T+1,K) )
bls=np.zeros( (T+1) )
b[-1,1:]=1./(K-1)
#hidden states
z=np.zeros( (T+1),dtype=np.int )
#expected hidden states
ex_k=np.zeros( (T,K) )
# expected pairs of hidden states
ex_kk=np.zeros( (K,K) )
nkk=np.zeros( (K,K) )
def fwd(xn):
global f,e
for t in xrange(T):
f[t+1,:]=np.dot(f[t,:],A)*e[t,:]
sm=np.sum(f[t+1,:])
fls[t+1]=fls[t]+np.log(sm)
f[t+1,:]/=sm
assert f[t+1,0]==0
def bck(xn):
global b,e
for t in xrange(T-1,-1,-1):
b[t,:]=np.dot(A,b[t+1,:]*e[t,:])
sm=np.sum(b[t,:])
bls[t]=bls[t+1]+np.log(sm)
b[t,:]/=sm
def em_step(xn):
global A,w,eta
global f,b,e,v
global ex_k,ex_kk,nkk
x=xn[:-1] #current data vectors
y=xn[1:,:1] #next data vectors predicted from current
#compute residuals
v=np.dot(x,w.T) # (N,K) <- (N,1) (N,K)
v-=y
e=np.exp(-eta/2*v**2,e)
fwd(xn)
bck(xn)
# compute expected hidden states
for t in xrange(len(e)):
ex_k[t,:]=f[t+1,:]*b[t+1,:]
ex_k[t,:]/=np.sum(ex_k[t,:])
# compute expected pairs of hidden states
for t in xrange(len(f)-1):
ex_kk=A*f[t,:][:,np.newaxis]*e[t,:]*b[t+1,:]
ex_kk/=np.sum(ex_kk)
nkk+=ex_kk
# max w/ respect to transition probabilities
A=pA+nkk
A/=np.sum(A,1)[:,np.newaxis]
# solve the weighted regression problem for emissions weights
# x and y are from above
for k in xrange(K):
ex=ex_k[:,k][:,np.newaxis]
dx=np.dot(x.T,ex*x)
dy=np.dot(x.T,ex*y)
dy.shape=(2)
w[k,:]=lin.solve(dx+lam*np.eye(x.shape[1]), dy)
#return the probability of the sequence (computed by the forward algorithm)
return fls[-1]
if __name__=='__main__':
#run the em algorithm
for i in xrange(20):
print em_step(x)
#get rough boundaries by taking the maximum expected hidden state for each position
r=np.arange(len(ex_k))[np.argmax(ex_k,1)<3]
#plot
plt.plot(range(T),x[1:,0])
yr=[np.min(x[:,0]),np.max(x[:,0])]
for i in r:
plt.plot([i,i],yr,'-r')
plt.show()
pourquoi ne pas utiliser un simple filtre assorti? Ou sa contrepartie statistique générale appelée corrélation croisée. Étant donné un modèle connu x(t) et une série de temps composé bruyant contenant votre modèle décalé dans a,b,...,z comme y(t) = x(t-a) + x(t-b) +...+ x(t-z) + n(t). La fonction de corrélation croisée entre x et y donner des sommets a,b, ...,z
Weka est une puissante collection de logiciels d'apprentissage automatique, et prend en charge certains outils d'analyse de séries chronologiques, mais je ne sais pas assez sur le terrain pour recommander une meilleure méthode. Cependant, il est basé sur Java; et vous pouvez appeler le code Java à partir de C/C++ sans grande agitation.
Les paquetspour la manipulation de séries chronologiques sont principalement destinés au marché boursier. J'ai suggéré Cronos dans les commentaires; I n'ayez aucune idée de comment faire la reconnaissance de modèle avec elle, au-delà de l'évident: n'importe quel bon modèle d'une longueur de votre série devrait être en mesure de prédire que, après de petites bosses à une certaine distance de la dernière petite bosse, de grandes bosses suivent. Qui est votre série d'expositions d'auto-similarité, et les modèles utilisés dans Cronos sont conçus pour modèle.
si cela ne vous dérange pas C#, vous devriez demander une version de TimeSearcher2 des gens de hcil-reconnaissance de modèle est, pour ce système, le dessin d'un motif ressemble, puis de vérifier si votre modèle est suffisamment général pour capturer la plupart des cas avec un faible taux de faux positifs. Probablement l'approche la plus conviviale que vous trouverez; tous les autres nécessitent tout à fait une base dans les statistiques ou les stratégies de reconnaissance de modèle.
Je ne suis pas sûr que quel paquet fonctionnerait le mieux pour cela. J'ai fait quelque chose de similaire à un moment à l'université où j'ai essayé de détecter automatiquement certaines formes similaires sur un axe x-y pour un tas de graphes différents. Vous pourriez faire quelque chose comme ce qui suit.
étiquettes de Classe comme:
- pas de classe
- début de la région
- centre de la région
- fin de région
caractéristiques comme:
- axe des y relatif différence relative et absolue de chacun des points environnants dans une fenêtre 11 points de large
- Fonctionnalités comme la différence de la moyenne
- différence Relative entre le point avant et le point après
j'utilise deep learning si c'est une option pour vous. C'est fait en Java, Deeplearning4j . J'expérimente avec LSTM. J'ai essayé 1 couche cachée et 2 couches cachées pour traiter les séries chronologiques.
return new NeuralNetConfiguration.Builder()
.seed(HyperParameter.seed)
.iterations(HyperParameter.nItr)
.miniBatch(false)
.learningRate(HyperParameter.learningRate)
.biasInit(0)
.weightInit(WeightInit.XAVIER)
.momentum(HyperParameter.momentum)
.optimizationAlgo(
OptimizationAlgorithm.STOCHASTIC_GRADIENT_DESCENT // RMSE: ????
)
.regularization(true)
.updater(Updater.RMSPROP) // NESTEROVS
// .l2(0.001)
.list()
.layer(0,
new GravesLSTM.Builder().nIn(HyperParameter.numInputs).nOut(HyperParameter.nHNodes_1).activation("tanh").build())
.layer(1,
new GravesLSTM.Builder().nIn(HyperParameter.nHNodes_1).nOut(HyperParameter.nHNodes_2).dropOut(HyperParameter.dropOut).activation("tanh").build())
.layer(2,
new GravesLSTM.Builder().nIn(HyperParameter.nHNodes_2).nOut(HyperParameter.nHNodes_2).dropOut(HyperParameter.dropOut).activation("tanh").build())
.layer(3, // "identity" make regression output
new RnnOutputLayer.Builder(LossFunctions.LossFunction.MSE).nIn(HyperParameter.nHNodes_2).nOut(HyperParameter.numOutputs).activation("identity").build()) // "identity"
.backpropType(BackpropType.TruncatedBPTT)
.tBPTTBackwardLength(100)
.pretrain(false)
.backprop(true)
.build();
Trouvé quelques petites choses:
- LSTM ou RNN est très bon, à choisir les modèles de la série temporelle.
- a essayé sur une série chronologique, et un groupe de différentes séries chronologiques. Modèle ont été choisi facilement.
- C'est aussi essayer de choisir des modèles pas pour juste un de la cadence. S'il y a des modèles par semaine, et par mois, les deux seront appris par le réseau.