Régression Non linéaire en C#
je cherche un moyen de produire une courbe non linéaire (de préférence quadratique), basée sur un ensemble de données 2D, à des fins de prédiction. En ce moment, j'utilise ma propre implémentation des moindres carrés ordinaires (MCO) pour produire une tendance linéaire, mais mes tendances sont beaucoup plus adaptées à un modèle de courbe. Les données que j'analyse sont la charge du système dans le temps.
Voici l'équation que j'utilise pour produire mes coefficients linéaires:
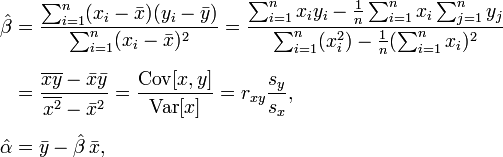
j'ai eu un coup d'oeil à Math.NET Numerics et quelques autres libs, mais ils fournissent interpolation au lieu de régression (ce qui ne me sert à rien), ou le code ne fonctionne pas d'une façon ou d'une autre.
Quelqu'un connaît des libs libres ou des échantillons de code qui peuvent produire les coefficients pour une telle courbe?
4 réponses
j'ai utilisé le MathNet.Iridium release car il est compatible avec .NET 3.5 et VS2008. La méthode est basée sur l' Vandermonde de la matrice. Puis j'ai créé une classe pour tenir ma régression polynomiale
using MathNet.Numerics.LinearAlgebra;
public class PolynomialRegression
{
Vector x_data, y_data, coef;
int order;
public PolynomialRegression(Vector x_data, Vector y_data, int order)
{
if (x_data.Length != y_data.Length)
{
throw new IndexOutOfRangeException();
}
this.x_data = x_data;
this.y_data = y_data;
this.order = order;
int N = x_data.Length;
Matrix A = new Matrix(N, order + 1);
for (int i = 0; i < N; i++)
{
A.SetRowVector( VandermondeRow(x_data[i]) , i);
}
// Least Squares of |y=A(x)*c|
// tr(A)*y = tr(A)*A*c
// inv(tr(A)*A)*tr(A)*y = c
Matrix At = Matrix.Transpose(A);
Matrix y2 = new Matrix(y_data, N);
coef = (At * A).Solve(At * y2).GetColumnVector(0);
}
Vector VandermondeRow(double x)
{
double[] row = new double[order + 1];
for (int i = 0; i <= order; i++)
{
row[i] = Math.Pow(x, i);
}
return new Vector(row);
}
public double Fit(double x)
{
return Vector.ScalarProduct( VandermondeRow(x) , coef);
}
public int Order { get { return order; } }
public Vector Coefficients { get { return coef; } }
public Vector XData { get { return x_data; } }
public Vector YData { get { return y_data; } }
}
ce qui alors je l'utilise comme ceci:
using MathNet.Numerics.LinearAlgebra;
class Program
{
static void Main(string[] args)
{
Vector x_data = new Vector(new double[] { 0, 1, 2, 3, 4 });
Vector y_data = new Vector(new double[] { 1.0, 1.4, 1.6, 1.3, 0.9 });
var poly = new PolynomialRegression(x_data, y_data, 2);
Console.WriteLine("{0,6}{1,9}", "x", "y");
for (int i = 0; i < 10; i++)
{
double x = (i * 0.5);
double y = poly.Fit(x);
Console.WriteLine("{0,6:F2}{1,9:F4}", x, y);
}
}
}
coefficients calculés de[1,0.57,-0.15] le résultat:
x y
0.00 1.0000
0.50 1.2475
1.00 1.4200
1.50 1.5175
2.00 1.5400
2.50 1.4875
3.00 1.3600
3.50 1.1575
4.00 0.8800
4.50 0.5275
qui correspond au quadratique résultats de Wolfram Alpha.
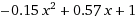
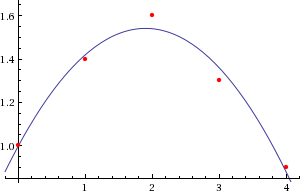
Edit 1
Pour obtenir de l'ajustement que vous voulez essayer l'initialisation suivante pour x_data et y_data:
Matrix points = new Matrix( new double[,] { { 1, 82.96 },
{ 2, 86.23 }, { 3, 87.09 }, { 4, 84.28 },
{ 5, 83.69 }, { 6, 89.18 }, { 7, 85.71 },
{ 8, 85.05 }, { 9, 85.58 }, { 10, 86.95 },
{ 11, 87.95 }, { 12, 89.44 }, { 13, 93.47 } } );
Vector x_data = points.GetColumnVector(0);
Vector y_data = points.GetColumnVector(1);
qui produit les coefficients suivants (de la puissance la plus faible à la puissance la plus élevée)
Coef=[85.892,-0.5542,0.074990]
x y
0.00 85.8920
1.00 85.4127
2.00 85.0835
3.00 84.9043
4.00 84.8750
5.00 84.9957
6.00 85.2664
7.00 85.6871
8.00 86.2577
9.00 86.9783
10.00 87.8490
11.00 88.8695
12.00 90.0401
13.00 91.3607
14.00 92.8312
le code@ja72 est assez bon. Mais je l'ai porté sur la version actuelle deMath.NET (MathNet.Iridium n'est pas supporté maintenant comme je comprends) et optimiser à la fois la taille du code et la performance (Math.La fonction Pow n'est pas utilisée dans ma solution à cause de la lenteur des performances).
public class PolynomialRegression
{
private int _order;
private Vector<double> _coefs;
public PolynomialRegression(DenseVector xData, DenseVector yData, int order)
{
_order = order;
int n = xData.Count;
var vandMatrix = new DenseMatrix(xData.Count, order + 1);
for (int i = 0; i < n; i++)
vandMatrix.SetRow(i, VandermondeRow(xData[i]));
// var vandMatrixT = vandMatrix.Transpose();
// 1 variant:
//_coefs = (vandMatrixT * vandMatrix).Inverse() * vandMatrixT * yData;
// 2 variant:
//_coefs = (vandMatrixT * vandMatrix).LU().Solve(vandMatrixT * yData);
// 3 variant (most fast I think. Possible LU decomposion also can be replaced with one triangular matrix):
_coefs = vandMatrix.TransposeThisAndMultiply(vandMatrix).LU().Solve(TransposeAndMult(vandMatrix, yData));
}
private Vector<double> VandermondeRow(double x)
{
double[] result = new double[_order + 1];
double mult = 1;
for (int i = 0; i <= _order; i++)
{
result[i] = mult;
mult *= x;
}
return new DenseVector(result);
}
private static DenseVector TransposeAndMult(Matrix m, Vector v)
{
var result = new DenseVector(m.ColumnCount);
for (int j = 0; j < m.RowCount; j++)
for (int i = 0; i < m.ColumnCount; i++)
result[i] += m[j, i] * v[j];
return result;
}
public double Calculate(double x)
{
return VandermondeRow(x) * _coefs;
}
}
il est aussi disponible sur GitHub:gist.
Je ne pense pas que vous vouliez une régression non linéaire. Même si vous utilisez une fonction quadratique, c'est encore appelée régression linéaire. Ce que vous voulez s'appelle la régression multivariée. Si vous voulez un quadratique, vous n'avez qu'à ajouter un terme X au carré à vos variables dépendantes.
je voudrais prendre un coup d'oeil à http://mathforum.org/library/drmath/view/53796.html pour essayer de se faire une idée de la façon dont il peut être fait.