Régression Linéaire: Normalisation De La Normalisation (Vs)
j'utilise la régression linéaire pour prédire les données. Mais j'obtiens des résultats totalement contrastés quand je normalise (Vs) standardiser les variables.
normalisation = x-xmin/ xmax – xmin Note zéro standardisation = x - xmean/ xstd
a) Also, when to Normalize (Vs) Standardize ?
b) How Normalization affects Linear Regression?
c) Is it okay if I don't normalize all the attributes/lables in the linear regression?
Merci, Santosh
2 réponses
notez que les résultats ne sont pas nécessairement si différents. Vous pourriez tout simplement avoir besoin de différents hyperparamètres pour les deux options pour donner des résultats similaires.
L'idéal est de tester ce qui fonctionne le mieux pour votre problème. Si vous ne pouvez pas vous le permettre pour une raison quelconque, la plupart des algorithmes bénéficieront probablement de la normalisation plus que de la normalisation.
Voir ici pour quelques exemples de cas où l'on devrait être préféré à autres:
par exemple, dans les analyses de regroupement, la normalisation peut être particulièrement cruciale pour comparer les similitudes entre les caractéristiques basées sur certaines mesures de distance. Un autre exemple important est l'analyse en composantes principales, où nous préférons habituellement la standardisation à L'échelle Min-Max, puisque nous nous intéressons aux composantes qui maximisent la variance (selon la question et si L'APC calcule les composantes via la matrice de corrélation au lieu de la matrice de covariance; mais plus sur la PCA dans mon précédent article).
cependant, cela ne signifie pas que la mise à l'échelle Min-Max n'est pas utile du tout! Une application populaire est le traitement d'image, où les intensités pixel doivent être normalisées pour s'adapter dans une certaine gamme (i.e., 0 à 255 pour la gamme de couleurs RGB). De plus, un algorithme de réseau neuronal typique requiert des données à une échelle de 0 à 1.
Un inconvénient de la normalisation sur la normalisation est qu'il perd informations dans les données, en particulier sur les valeurs aberrantes.
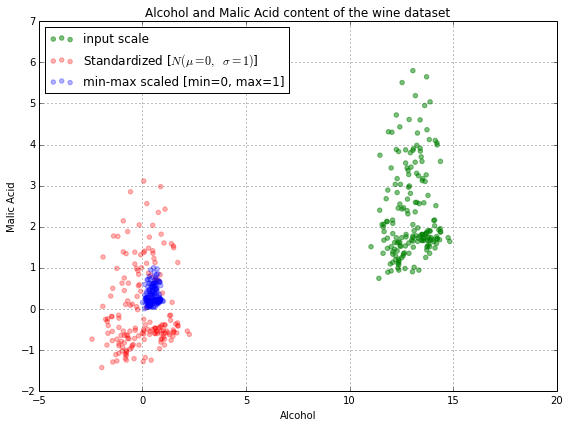
aussi sur la page liée, il y a cette image:
comme vous pouvez le voir, la mise à l'échelle regroupe toutes les données très près les unes des autres, ce qui n'est peut-être pas ce que vous voulez. Cela pourrait faire en sorte que des algorithmes comme le gradient de descente mettent plus de temps à converger vers la même solution qu'ils le feraient sur un ensemble de données standardisé, ou cela pourrait même le rendre impossible.
"Normalisation les variables" n'a pas vraiment de sens. La terminologie correcte est "normalisation / mise à l'échelle des caractéristiques". Si vous voulez normaliser ou mettre à l'échelle une fonctionnalité, vous devriez faire la même chose pour le reste.
cela a du sens parce que la normalisation et la normalisation font des choses différentes.
la normalisation transforme vos données en une plage de 0 à 1
la standardisation transforme vos données de telle sorte que la distribution résultante a une moyenne de 0 et un écart-type de 1
normalisation/normalisation sont conçus pour atteindre un objectif similaire, qui est de créer des caractéristiques qui ont des gammes similaires à l'autre. Nous le voulons pour être sûrs que nous capturent l'information vraie dans une fonctionnalité, et que nous ne surestimons pas une fonctionnalité particulière juste parce que ses valeurs sont beaucoup plus grandes que d'autres fonctionnalités.
si toutes vos fonctionnalités sont dans une plage similaire les unes des autres, alors il n'y a pas vraiment besoin de standardiser/normaliser. Si, cependant, certaines fonctionnalités prennent naturellement des valeurs beaucoup plus grandes/plus petites que d'autres, alors la normalisation / normalisation est nécessaire
si vous devez normaliser au moins un variable/fonction, je ferais la même chose à tous les autres