K-Means: Lloyd, Forgy, MacQueen, Hartigan-Wong

R fournit L'algorithme de Lloyd comme option à kmeans (); l'algorithme par défaut, par Hartigan et Wong (1979) sont beaucoup plus intelligents. Comme l'algorithme de MacQueen (MacQueen, 1967 )), il met à jour les centroïdes chaque fois qu'un point est déplacé; il fait également des choix intelligents (gain de temps) dans la vérification de l'amas le plus proche. D'un autre côté, L'algorithme de Lloyd K-means est le premier et le plus simple de tous ces algorithmes de regroupement.

L'algorithme de Lloyd (Lloyd, 1957) prend un ensemble de des observations ou des cas (penser: des rangées de une matrice nxp, ou points in Reals) et les regroupe en k groupes. Il essaie de minimiser les au sein d'un cluster somme des carrés

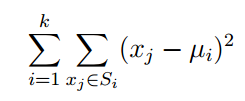
où u_i est la moyenne de tous les points du groupe S_i. L'algorithme se déroule comme suit (je vais vous épargner la formalité de la notation exhaustive):

il y a un problème avec la mise en oeuvre de R, cependant, et le problème se pose quand compte tenu de multiples les points de départ. Je dois noter qu'il est généralement prudent de considérer diérents points de départ, parce que l'algorithme est garanti à converger, mais n'est pas garanti pour couvrir un optima global. C'est particulièrement vrai pour les grands, de grande dimension problème. Je vais commencer par un exemple simple (grand, pas particulièrement dicult).

(ici je vais coller quelques images car nous ne pouvons pas écrire des formulas mathématiques avec le latex)

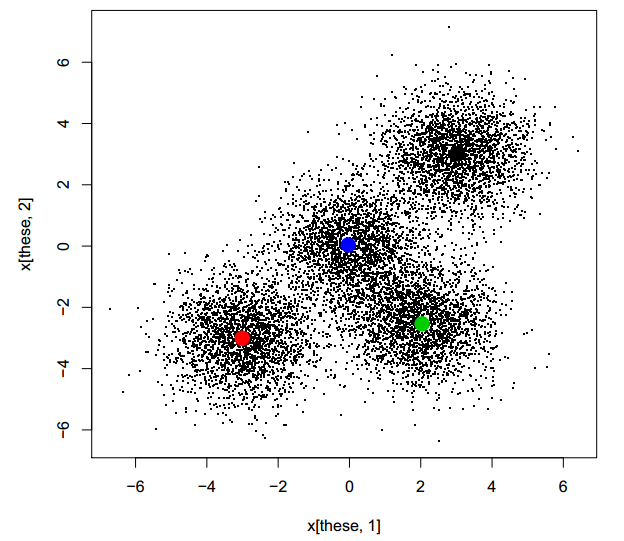
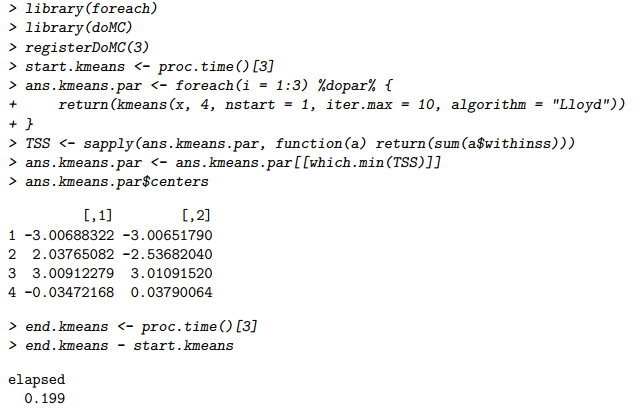
notez que la solution est très similaire à celle obtenue antérieurement, bien que l'ordre des clusters est arbitraire. Plus important encore, le travail n'a pris que 0,199 secondes en parallèle! Sûrement c'est trop beau pour être vrai: l'utilisation de 3 cœurs de processeur devrait, au mieux, prendre un tiers de la Heure de notre première course (séquentielle). Est-ce un problème? On dirait un déjeuner gratuit. Il n'y a pas de problème avec un déjeuner gratuit de temps en temps, n'est-ce pas?

cela ne fonctionne pas toujours avec les fonctions R, mais parfois nous avons la chance de regarder directement dans le code. C'est un de ces moments. Je vais mettre ce code en file, mykmeans.R, et l'éditer à la main, en insérant des instructions cat() à différents endroits. Voici une façon intelligente de faire ceci, en utilisant sink () (bien que cela ne semble pas fonctionner en Sweave, cela fonctionnera de manière interactive):

> sink("mykmeans.R")
> kmeans
> sink()

Maintenant éditer le fichier, changer le nom de la fonction et ajouter des instructions cat (). Note que vous devez également supprimer une ligne de remorquage: :

nous pouvons alors répéter nos explorations, mais en utilisant mykmeans ():

> source("mykmeans.R")
> start.kmeans <- proc.time()[3]
> ans.kmeans <- mykmeans(x, 4, nstart = 3, iter.max = 10, algorithm = "Lloyd")
JJJ statement 1: 0 elapsed time.
JJJ statement 5: 2.424 elapsed time.
JJJ statement 6: 2.425 elapsed time.
JJJ statement 7: 2.52 elapsed time.
JJJ statement 6: 2.52 elapsed time.
JJJ statement 7: 2.563 elapsed time.

maintenant nous sommes dans les affaires: la plupart du temps a été consommé avant l'état 5 (je savais cela de bien sûr, c'est pourquoi l'énoncé 5 était 5 plutôt que 2)... Vous pouvez continuer à jouer avec

Voici le code:

#######################################################################
# kmeans()

N <- 100000
x <- matrix(0, N, 2)
x[seq(1,N,by=4),] <- rnorm(N/2)
x[seq(2,N,by=4),] <- rnorm(N/2, 3, 1)
x[seq(3,N,by=4),] <- rnorm(N/2, -3, 1)
x[seq(4,N,by=4),1] <- rnorm(N/4, 2, 1)
x[seq(4,N,by=4),2] <- rnorm(N/4, -2.5, 1)
start.kmeans <- proc.time()[3]
ans.kmeans <- kmeans(x, 4, nstart=3, iter.max=10, algorithm="Lloyd")
ans.kmeans$centers
end.kmeans <- proc.time()[3]
end.kmeans - start.kmeans

these <- sample(1:nrow(x), 10000)
plot(x[these,1], x[these,2], pch=".")
points(ans.kmeans$centers, pch=19, cex=2, col=1:4)

library(foreach)
library(doMC)
registerDoMC(3)
start.kmeans <- proc.time()[3]
ans.kmeans.par <- foreach(i=1:3) %dopar% {
  return(kmeans(x, 4, nstart=1, iter.max=10, algorithm="Lloyd"))
}
TSS <- sapply(ans.kmeans.par, function(a) return(sum(a$withinss)))
ans.kmeans.par <- ans.kmeans.par[[which.min(TSS)]]
ans.kmeans.par$centers
end.kmeans <- proc.time()[3]
end.kmeans - start.kmeans

sink("mykmeans.Rfake")
kmeans
sink()

source("mykmeans.R")
start.kmeans <- proc.time()[3]
ans.kmeans <- mykmeans(x, 4, nstart=3, iter.max=10, algorithm="Lloyd")
ans.kmeans$centers
end.kmeans <- proc.time()[3]
end.kmeans - start.kmeans

#######################################################################
# Diving

x <- read.csv("Diving2000.csv", header=TRUE, as.is=TRUE)
library(YaleToolkit)
whatis(x)

x[1:14,c(3,6:9)]

meancol <- function(scores) {
  temp <- matrix(scores, length(scores)/7, ncol=7)
  means <- apply(temp, 1, mean)
  ans <- rep(means,7)
  return(ans)
}
x$panelmean <- meancol(x$JScore)

x[1:14,c(3,6:9,11)]

meancol <- function(scores) {
  browser()
  temp <- matrix(scores, length(scores)/7, ncol=7)
  means <- apply(temp, 1, mean)
  ans <- rep(means,7)
  return(ans)
}

x$panelmean <- meancol(x$JScore)

Voici la description:

Number of cases: 10,787 scores from 1,541 dives (7 judges score each
dive) performed in four events at the 2000 Olympic Games in Sydney,
Australia.

Number of variables: 10.

Description: A full description and analysis is available in an
article in The American Statistician (publication details to be
announced).

Variables:

Event       Four events, men's and women's 3M and 10m.
Round       Preliminary, semifinal, and final rounds.
Diver       The name of the diver.
Country     The country of the diver.
Rank        The final rank of the diver in the event.
DiveNo      The number of the dive in sequence within round.
Difficulty  The degree of difficulty of the dive.
JScore      The score provided for the judge on this dive.
Judge       The name of the judge.
JCountry    The country of the judge.

dataset Et de les expérimenter à https://www.dropbox.com/s/urgzagv0a22114n/Diving2000.csv

aller à la page 16-

Ceci a une explication claire de Gorgy / Llyods, MacQueen, hatigan-Wong algos.

https://core.ac.uk/download/pdf/27210461.pdf