Problème dans la formation caché markov modèle et l'utilisation pour la classification

au Lieu de répondre à chaque question, permettez-moi d'illustrer comment utiliser le HMM boîte à outils avec un exemple-- exemple de temps qui est habituellement utilisé lors de l'introduction de modèles markov cachés.

Fondamentalement, les états du modèle sont les trois types possibles de la météo: ensoleillé, pluvieux et brumeux. À n'importe quel jour, nous supposons que le temps peut être seulement une de ces valeurs. Ainsi, L'ensemble des États HMM sont:

S = {sunny, rainy, foggy}

Cependant dans cet exemple, nous ne pouvons pas observer la météo directement (apparemment nous sommes enfermés dans le sous-sol!). Au lieu de cela, la seule preuve que nous avons est de savoir si la personne qui vous surveille tous les jours porte un parapluie ou non. En terminologie HMM, ce sont les observations discrètes:

x = {umbrella, no umbrella}

le modèle HMM se caractérise par trois choses:

• Les probabilités antérieures: vecteur des probabilités d'être dans le premier état d'une séquence.
• le prob de transition: matrice décrivant les probabilités de passer d'un État météorologique à un autre.
• le prob d'émission: matrice décrivant les probabilités d'observation d'une sortie (globale ou non) donnée par un État (météo).

ensuite, soit on nous donne ces probabilités, soit on doit les apprendre d'un entraînement. Une fois que c'est fait, nous pouvons faire le raisonnement comme le calcul de la probabilité d'une séquence d'observation par rapport à un modèle HMM (ou un tas de modèles, et de choisir le plus probable)...

1) paramètres connus du modèle

Voici un exemple de code qui montre comment combler les probabilités pour construire le modèle:

Q = 3;    %# number of states (sun,rain,fog)
O = 2;    %# number of discrete observations (umbrella, no umbrella)

%#  prior probabilities
prior = [1 0 0];

%# state transition matrix (1: sun, 2: rain, 3:fog)
A = [0.8 0.05 0.15; 0.2 0.6 0.2; 0.2 0.3 0.5];

%# observation emission matrix (1: umbrella, 2: no umbrella)
B = [0.1 0.9; 0.8 0.2; 0.3 0.7];

alors nous pouvons échantillonner un tas de séquences de ce modèle:

num = 20;           %# 20 sequences
T = 10;             %# each of length 10 (days)
[seqs,states] = dhmm_sample(prior, A, B, num, T);

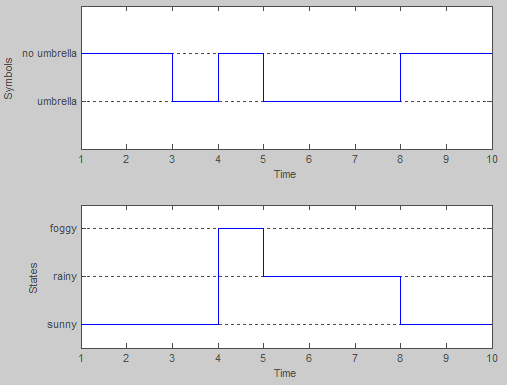
par exemple, la 5ème exemple a:

>> seqs(5,:)        %# observation sequence
ans =
     2     2     1     2     1     1     1     2     2     2

>> states(5,:)      %# hidden states sequence
ans =
     1     1     1     3     2     2     2     1     1     1

nous pouvons évaluer la log-vraisemblance de la séquence:

dhmm_logprob(seqs(5,:), prior, A, B)

dhmm_logprob_path(prior, A, B, states(5,:))

ou calculer le chemin de Viterbi (le plus probable état de la séquence):

vPath = viterbi_path(prior, A, multinomial_prob(seqs(5,:),B))

2) paramètres inconnus du modèle

la formation est effectuée à L'aide de L'algorithme EM, et le mieux est de faire avec un set de séquences d'observation.

en continuant sur le même exemple, nous pouvons utiliser les données générées ci-dessus pour former un nouveau modèle et le comparer à l'original:

%# we start with a randomly initialized model
prior_hat = normalise(rand(Q,1));
A_hat = mk_stochastic(rand(Q,Q));
B_hat = mk_stochastic(rand(Q,O));  

%# learn from data by performing many iterations of EM
[LL,prior_hat,A_hat,B_hat] = dhmm_em(seqs, prior_hat,A_hat,B_hat, 'max_iter',50);

%# plot learning curve
plot(LL), xlabel('iterations'), ylabel('log likelihood'), grid on

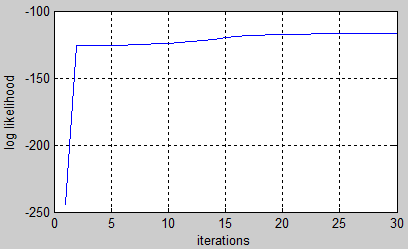
gardez à l'esprit que l'ordre des États ne doivent correspondre. C'est pourquoi nous devons permuter les états avant de comparer les deux modèles. Dans cet exemple, le modèle formé ressemble à celui d'origine:

>> p = [2 3 1];              %# states permutation

>> prior, prior_hat(p)
prior =
     1     0     0
ans =
      0.97401
  7.5499e-005
      0.02591

>> A, A_hat(p,p)
A =
          0.8         0.05         0.15
          0.2          0.6          0.2
          0.2          0.3          0.5
ans =
      0.75967      0.05898      0.18135
     0.037482      0.77118      0.19134
      0.22003      0.53381      0.24616

>> B, B_hat(p,[1 2])
B =
          0.1          0.9
          0.8          0.2
          0.3          0.7
ans =
      0.11237      0.88763
      0.72839      0.27161
      0.25889      0.74111

il y a plus de choses que vous pouvez faire avec les modèles markov cachés tels que la classification ou la reconnaissance de modèle. Vous auriez différents ensembles de séquences d'obervation appartenant à différentes classes. Vous commencez par former un modèle pour chaque ensemble. Ensuite, avec une nouvelle séquence d'observation, vous pouvez classer il calcule sa vraisemblance par rapport à chaque modèle et prédit le modèle ayant la plus forte probabilité logarithmique.

argmax[ log P(X|model_i) ] over all model_i