Comment comprendre le hachage sensible à la localité?
J'ai remarqué que LSH semble un bon moyen de trouver des éléments similaires avec des propriétés de grande dimension.
Après avoir lu le papier http://www.slaney.org/malcolm/yahoo/Slaney2008-LSHTutorial.pdf , je suis toujours confondu avec ces formules.
Est-ce que quelqu'un connaît un blog ou un article qui explique que le moyen facile?
5 réponses
Le meilleur tutoriel que j'ai vu pour LSH est dans le livre: Mining of Massive Datasets. Consultez Le Chapitre 3-Trouver Des Éléments Similaires http://infolab.stanford.edu / ~ ullman / mmds / ch3a. pdf
Je recommande également la diapositive ci-dessous: http://www.cs.jhu.edu/%7Evandurme/papers/VanDurmeLallACL10-slides.pdf . L'exemple dans la diapositive m'aide beaucoup à comprendre le hachage pour la similitude des cosinus.
J'emprunte deux diapositives de Benjamin Van Durme & Ashwin Lall, ACL2010 et essayez d'expliquer un peu les intuitions des familles LSH pour la Distance cosinus.
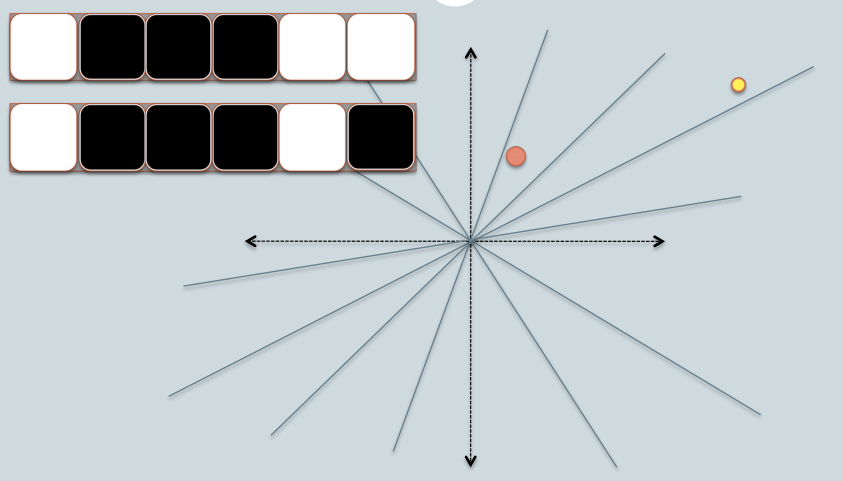
- sur la figure, il y a deux cercles avec Rouge etjaune colorés, représentant deux points de données bidimensionnels. Nous essayons de trouver leur similarité cosinus en utilisant LSH.
- les lignes grises sont des plans uniformément choisis au hasard.
- selon que le point de données se situe au-dessus ou au-dessous d'une ligne grise, nous marquons cette relation comme 0/1.
- dans le coin supérieur gauche, il y a deux rangées de carrés blancs/noirs, représentant respectivement la signature des deux points de données. Chaque carré correspond à un bit 0(blanc) ou 1(noir).
- donc, une fois que vous avez un pool d'avions, vous pouvez encoder les points de données avec leur emplacement respectif aux plans. Imaginez que lorsque nous avons plus de plans dans le pool, La différence angulaire codée dans la signature est plus proche de la différence réelle. Parce que seuls les avions qui résident entre les deux points donnera les deux données différentes valeur de bits.
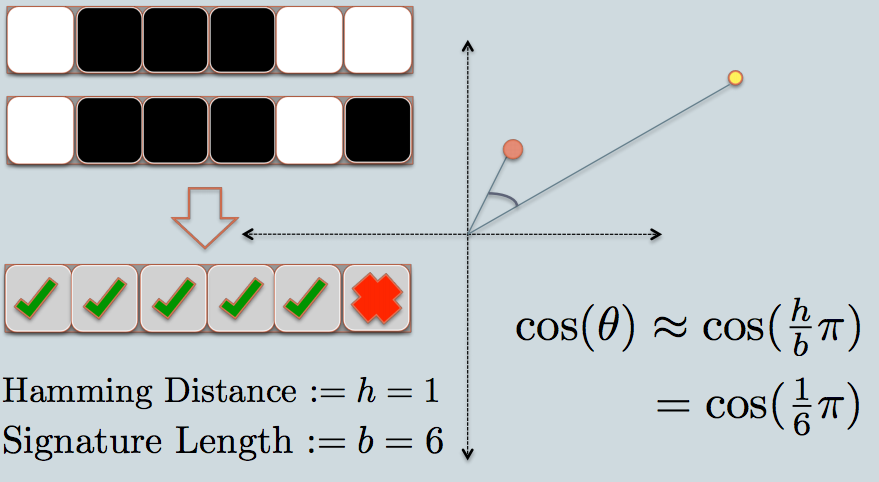
- maintenant, nous regardons la signature des deux points de données. Comme dans l'exemple, nous n'utilisons que 6 bits (carrés) pour représenter chaque donnée. C'est le hachage LSH pour les données d'origine que nous avons.
- la distance de hamming entre les deux valeurs hachées est 1, car leurs signatures ne diffèrent que de 1 bit.
- compte tenu de la longueur de la signature, on peut calculer leur similarité angulaire comme le montre le graphique.
J'ai un exemple de code (seulement 50 lignes) en python ici qui utilise la similarité cosinus. https://gist.github.com/94a3d425009be0f94751
Les Tweets dans l'espace vectoriel peuvent être un excellent exemple de données dimensionnelles élevées.
Consultez mon article de blog sur l'application du hachage sensible à la localité aux tweets pour en trouver des similaires.
Http://micvog.com/2013/09/08/storm-first-story-detection/
Et parce qu'une image est un millier de mots vérifier l'image ci-dessous:
Http://micvog.files.wordpress.com/2013/08/lsh1.png
J'espère que ça aide. @mvogiatzis
Voici une présentation de Stanford qui l'explique. Cela a fait une grande différence pour moi. La deuxième partie est plus sur LSH, mais la première partie le couvre aussi.
Une image de la vue d'ensemble (il y a beaucoup plus dans les diapositives):
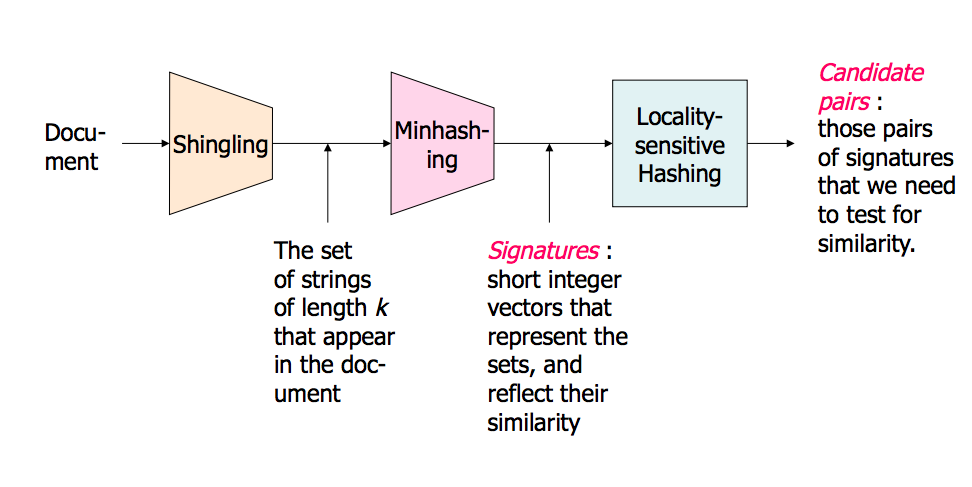
Recherche de voisin proche dans les données de dimensions élevées-Part1: http://www.stanford.edu/class/cs345a/slides/04-highdim.pdf
Recherche de voisin proche dans des données de dimensions élevées - Part2: http://www.stanford.edu/class/cs345a/slides/05-LSH.pdf
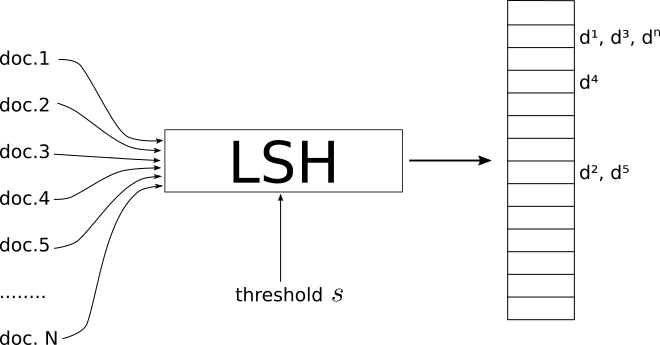
- LSH est une procédure qui prend comme entrée un ensemble de documents / images / objets et génère une sorte de Table de hachage.
- Les indices de ce tableau contiennent les documents tels que les documents qui sont sur le même indice sont considérés comme semblable et ceux sur les différents indices sont "dissemblables".
- Où similar dépend du système métrique et aussi d'une similarité de seuil s qui agit comme un paramètre global de LSH.
- Il est jusqu'à vous pouvez définir quel est le seuil adéquat s pour votre problème.
Il est important de souligner que différentes mesures de similarité ont des implémentations différentes de LSH.
Dans mon blog, j'ai essayé d'expliquer en détail LSH pour les cas de minHashing (mesure de similarité jaccard) et simHashing (mesure de distance cosinus). J'espère que vous la trouverez utile: https://aerodatablog.wordpress.com/2017/11/29/locality-sensitive-hashing-lsh/
Je suis une personne visuelle. Voici ce qui fonctionne pour moi comme une intuition.
Dites que chacune des choses que vous voulez rechercher approximativement sont des objets physiques tels qu'une pomme, un cube, une chaise.
Mon intuition pour un LSH est qu'il est similaire de prendre les ombres de ces objets. Si vous prenez l'ombre d'un cube 3D vous obtenez un 2D carré, comme sur un morceau de papier, ou d'une sphère en 3D, vous obtiendrez un cercle de l'ombre sur un morceau de papier.
Finalement, il y a beaucoup plus de trois dimensions dans un problème de recherche (où chaque mot dans un texte pourrait être une dimension) mais l'analogie shadow m'est toujours très utile.
Maintenant, nous pouvons comparer efficacement les chaînes de bits dans le logiciel. Une chaîne de bits de longueur fixe est un peu, plus ou moins, comme une ligne dans une seule dimension.
Donc, avec un LSH, je projette les ombres des objets éventuellement sous forme de points (0 ou 1) sur une seule ligne/chaîne de bits de longueur fixe.
Toute L'astuce est de prendre les ombres telles que ils ont toujours un sens dans la dimension inférieure, par exemple ils ressemblent à l'objet original d'une manière assez bonne qui peut être reconnue.
UN dessin 2D d'un cube en perspective me dit que c'est un cube. Mais je ne peux pas distinguer facilement un carré 2D d'une ombre de cube 3D sans perspective: ils ressemblent tous deux à un carré pour moi.
La façon dont je présente mon objet à la lumière déterminera si j'obtiens une bonne ombre reconnaissable ou non. Donc, je pense à un" bon " LSH comme celui qui va transformer mon objets devant une lumière telle que leur ombre est mieux reconnaissable comme représentant mon objet.
Donc pour récapituler: je pense aux choses à indexer avec un LSH comme des objets physiques comme un cube, une table ou une chaise, et je projette leurs ombres en 2D et éventuellement le long d'une ligne (une chaîne de bits). Et une "bonne" fonction LSH est la façon dont je présente mes objets devant une lumière pour obtenir une forme approximativement distinguable dans le flatland 2D et plus tard ma chaîne de bits.
Enfin quand je veux rechercher si un objet que j'ai est similaire à certains objets que j'ai indexés, je prends les ombres de cet objet "requête" en utilisant la même manière pour présenter mon objet devant la lumière (éventuellement se retrouver avec une chaîne de bits aussi). Et maintenant, je peux comparer à quel point cette chaîne de bits est similaire à toutes mes autres chaînes de bits indexées qui est un proxy pour rechercher mes objets entiers si j'ai trouvé un moyen bon et reconnaissable de présenter mes objets à ma lumière.