Comment trouver la distribution de probabilité et les paramètres pour les données réelles? (Python 3)

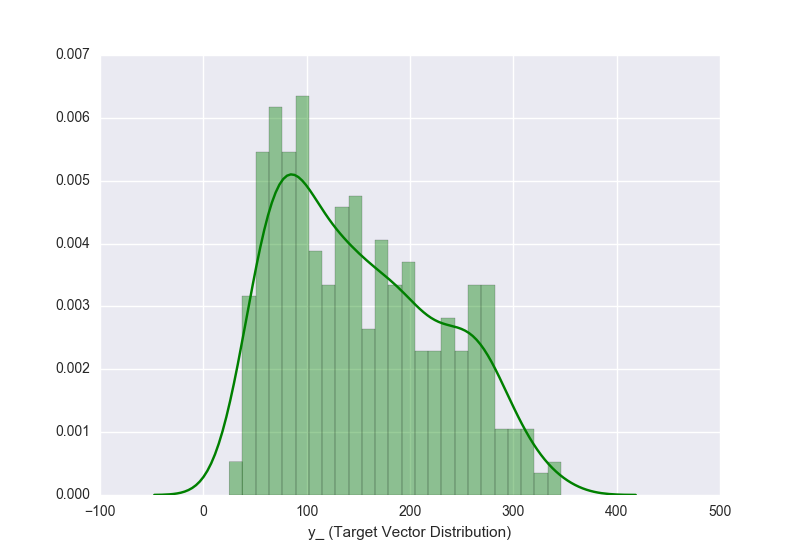
j'ai un ensemble de données de sklearn et j'ai tracé la distribution de l' load_diabetes.target données (c'est-à-dire les valeurs de la régression que le load_diabetes.data sont utilisés pour prédire).

j'ai utilisé ce parce qu'il a le plus petit nombre de variables/les attributs de la régression sklearn.datasets.

Utilisant Python 3,Comment puis-je obtenir le type de distribution et les paramètres de la distribution la plus proche?

Tout ce que je sais target les valeurs sont toutes positives et biaisé (positve inclinaison droite/inclinaison). . . Est-il possible en Python de fournir quelques distributions et ensuite d'obtenir le meilleur ajustement pour l' target données/vecteur? Ou pour suggérer un ajustement basé sur les données fournies? Cela serait très utile pour les personnes qui ont une connaissance théorique de la statistique mais peu d'expérience de son application aux "données réelles".

Bonus Serait-il judicieux d'utiliser ce type d'approche pour comprendre ce que votre la distribution postérieure serait avec "données réelles"? Si non, pourquoi pas?

from sklearn.datasets import load_diabetes
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import pandas as pd

#Get Data
data = load_diabetes()
X, y_ = data.data, data.target

#Organize Data
SR_y = pd.Series(y_, name="y_ (Target Vector Distribution)")

#Plot Data
fig, ax = plt.subplots()
sns.distplot(SR_y, bins=25, color="g", ax=ax)
plt.show()

enter image description here

17
demandé sur O.rka 2016-05-27 18:58:31

3 réponses

au meilleur de ma connaissance, il n'existe pas de moyen automatique d'obtenir le type de distribution et les paramètres d'un échantillon (inférer

À mon avis, le meilleur que vous pouvez faire c'est:

(pour chaque attribut)

  • essayez d'ajuster chaque attribut à une liste assez large de distributions possibles (voir, par exemple, ajustement de la distribution empirique aux données théoriques avec Scipy (Python)? pour un exemple avec Scipy)

  • évaluez toutes vos crises et choisissez la meilleure. Cela peut être fait en effectuant un test de Kolmogorov-Smirnov entre votre échantillon et chacune des distributions de l'ajustement (vous avez une implémentation en Scipy, encore une fois), et en choisissant celle qui minimise D, la statistique de test (A. K. A. la différence entre l'échantillon et l'ajustement).

Bonus: cela aurait du sens - comme vous le construirez un modèle sur chacune des variables lorsque vous choisissez un ajustement pour chacune d'elles - bien que la qualité de votre prédiction dépende de la qualité de vos données et des distributions que vous utilisez pour ajuster. Vous êtes à la construction d'un modèle, après tout.

9
répondu carrdelling 2017-05-23 12:08:02

Vous pouvez utiliser ce code pour ajuster (selon le maximum de vraisemblance) différentes distributions avec vos données:

import matplotlib.pyplot as plt
import scipy
import scipy.stats

dist_names = ['gamma', 'beta', 'rayleigh', 'norm', 'pareto']

for dist_name in dist_names:
    dist = getattr(scipy.stats, dist_name)
    param = dist.fit(y)
    # here's the parameters of your distribution, scale, location

Vous pouvez voir un extrait d'exemple sur la façon d'utiliser les paramètres obtenus ici: ajustement de la distribution empirique aux distributions théoriques avec Scipy (Python)?

alors, vous pouvez choisir la distribution avec la meilleure probabilité logarithmique (il y a aussi d'autres critères pour correspondre à la "meilleure" distribution, tels que le postérieur bayésien probabilité, valeurs AIC, BIC ou BICc,...).

pour votre question bonus, il n'y a pas de réponse générique. Si votre ensemble de données est significatif et obtenu dans les mêmes conditions le mot réel des données, vous pouvez le faire.

5
répondu Alexis Clarembeau 2017-05-23 12:22:39

Utilisez cette approche

def get_best_distribution(data):
    dist_names = ["norm", "exponweib", "weibull_max", "weibull_min", "pareto", "genextreme"]
    dist_results = []
    params = {}
    for dist_name in dist_names:
        dist = getattr(st, dist_name)
        param = dist.fit(data)

        params[dist_name] = param
        # Applying the Kolmogorov-Smirnov test
        D, p = st.kstest(data, dist_name, args=param)
        print("p value for "+dist_name+" = "+str(p))
        dist_results.append((dist_name, p))

    # select the best fitted distribution
    best_dist, best_p = (max(dist_results, key=lambda item: item[1]))
    # store the name of the best fit and its p value

    print("Best fitting distribution: "+str(best_dist))
    print("Best p value: "+ str(best_p))
    print("Parameters for the best fit: "+ str(params[best_dist]))

    return best_dist, best_p, params[best_dist]
2
répondu Pasindu Tennage 2018-08-08 08:51:22