Comment calculer le paramètre de régularisation dans la régression linéaire

CLOSED FORM (TIKHONOV) VERSUS GRADIENT DESCENT

Salut! belles explications pour les approches mathématiques intuitives et de premier ordre là. Je voulais juste ajouter quelques spécificités qui, lorsqu'elles ne sont pas "résolution de problèmes", peuvent certainement aider à accélérer et donner une certaine cohérence au processus de trouver un bon hyperparamètre de régularisation.

je suppose que tu parles de L2 (A. K." perte de poids") régularisation, pondérée linéairement par lambda et que vous optimisez les poids de votre modèle soit avec le fermé forme Tikhonov équation (fortement recommandé pour les modèles de régression linéaire à faible dimension), ou avec une variante de descente en pente avec rétropropagation. Et que, dans ce contexte, vous voulez choisir la valeur de lambda qui offre la meilleure capacité de généralisation.

FERMÉ FORME (TIKHONOV)

si vous êtes capable de suivre la voie de Tikhonov avec votre modèle ( Andrew Ng dit sous les dimensions de 10k, mais cette suggestion a au moins 5 ans)Wikipédia - détermination du facteur de Tikhonov offre un intéressant solution à forme fermée, dont il a été prouvé qu'elle fournit la valeur optimale. Mais cette solution soulève probablement des problèmes de mise en œuvre (complexité temporelle/stabilité numérique) dont je ne suis pas au courant., car il n'est pas courant dominant de l'algorithme à exécuter. Ce 2016 papier semble très prometteur cependant et peut-être vaut-il la peine d'essayer si vous devez vraiment optimiser votre modèle linéaire à son meilleur.

• For a quickly prototype implementation, this 2015 paquet Python semble traiter avec elle de manière itérative, vous pouvez laisser optimiser et puis d'en extraire de la valeur finale pour le lambda:

Dans cette nouvelle méthode innovante, nous ont dérivé une approche itérative pour résoudre le problème général de régularisation Tikhonov, qui converge à la solution sans bruit, ne dépend pas fortement sur le choix de lambda, et pourtant évite le problème d'inversion.

Et de la GitHub README du projet: InverseProblem.invert(A, be, k, l) #this will invert your A matrix, where be is noisy be, k is the no. of iterations, and lambda is your dampening effect (best set to 1)

DESCENTE EN PENTE

tous les liens de cette partie sont de Michael Nielsen l'incroyable livre en ligne "Neural Networks et l'Apprentissage en Profondeur", a recommandé la conférence!

pour cette approche, il semble être encore moins à dire: la fonction de coût est généralement non convexe, l'optimisation est réalisée numériquement et la performance du modèle est mesurée par une certaine forme de validation croisée (voir Survitting and Regularization et pourquoi la régularisation aide-t-elle à réduire le surpâturage si vous n'en avez pas assez). Mais même en cas de validation croisée, Nielsen suggère quelque chose: vous pouvez prendre un coup d'oeil à cette explication détaillée sur comment la régularisation L2 fournir un poids décomposition de l'effet, mais le résumé est que c'est inversement proportionnelle au nombre d'échantillons n, donc lors du calcul de l'équation de pente de descente avec le terme L2,

utilisez simplement la rétropagation, comme d'habitude, puis ajoutez (λ/n)*w pour la dérivée partielle de tout le poids terme.

et sa conclusion est que, si l'on veut un effet de régularisation similaire avec un nombre différent d'échantillons, lambda doit être changé proportionnellement:

nous devons modifier le paramètre de régularisation. La raison en est que la taille n de l'ensemble de la formation a changé à partir de n=1000n=50000, et cela modifie le poids decay 1−learning_rate*(λ/n). Si nous avons continué à utiliser λ=0.1 cela signifierait beaucoup moins de perte de poids, et donc encore moins un effet de régularisation. Nous indemniser en changeant λ=5.0.

ceci n'est utile que lorsque l'on applique le même modèle à différentes quantités des mêmes données, mais je pense que cela ouvre la porte à une certaine intuition sur la façon dont cela devrait fonctionner, et, plus important encore, accélère le processus d'hyperparamétrisation en vous permettant de finetune lambda dans des sous-ensembles plus petits, puis de mettre à l'échelle.

pour le choix des valeurs exactes, il suggère dans ses conclusions comment choisir les hyperparamètres d'un réseau neuronal l'approche purement empirique: commencer par 1 et ensuite multiplier et diviser progressivement par 10 jusqu'à trouver l'ordre de grandeur approprié, puis faire une recherche locale dans cette région. Dans les commentaires cela SE liés à la question, L'utilisateur Brian Borchers suggère également une méthode très bien connue qui pourrait être utile pour cette recherche locale:

1. Prendre de petits sous-ensembles de la formation et de la validation jeux (pour être en mesure de faire beaucoup d'entre eux dans un délai raisonnable)
2. Commençant par λ=0 et augmentant de petites quantités dans une certaine région, effectuer une formation rapide&validation du modèle et tracer les deux fonctions de perte
3. vous observerez trois choses:
   1. la fonction de perte de CV sera toujours plus élevée que la fonction de formation, puisque votre modèle est optimisé pour les données de formation exclusivement (EDIT: Après quelque temps, j'ai vu un MNIST cas où l'ajout de L2 a aidé la perte de CV à diminuer plus rapidement que celui de la formation jusqu'à la convergence. Probablement en raison de la cohérence ridicule des données et d'une hyperparamétrisation sous-optimale par contre).
   2. la fonction de perte d'entraînement aura son minimum pour λ=0, puis augmentent avec la régularisation, car empêcher le modèle d'ajuster de façon optimale les données de formation est exactement ce que fait la régularisation.
   3. la fonction de perte de CV démarre haut à λ=0, puis décroissent, puis recommencent à augmenter à un certain point (EDIT: ceci en supposant que le setup est en mesure de overfit pour λ=0, c'est-à-dire que le modèle a assez de puissance et qu'aucun autre moyen de régularisation n'est appliqué de façon trop importante).
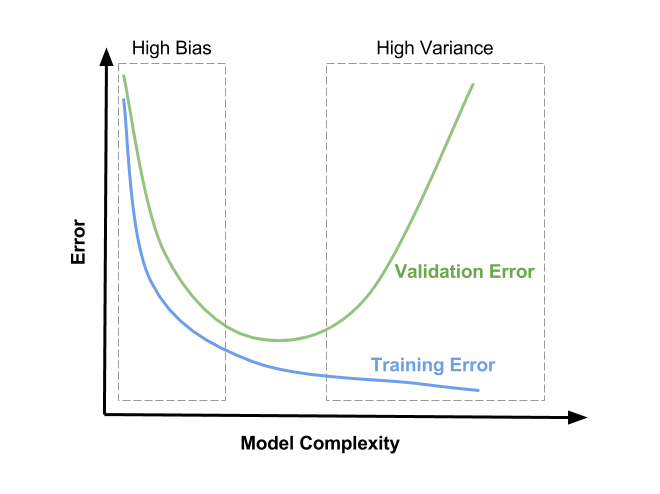
4. La valeur optimale pour λ sera probablement quelque part autour du minimum de la fonction de perte de CV, il peut également dépendre un peu sur la façon dont la fonction de perte d'entraînement ressemble. Voir la photo pour une possible (mais pas la seule) représentation de ceci: au lieu de "complexité du modèle" vous devriez interpréter l'axe x λ être zéro à droite et augmenter vers la gauche.

Espérons que cette aide! Acclamations,