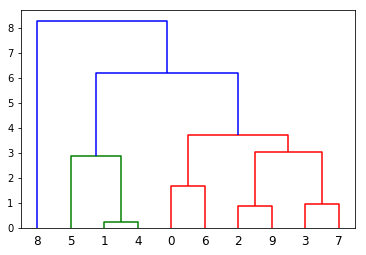
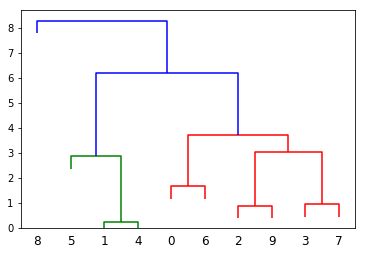
Comment ajuster la longueur des branches du dendrogramme dans matplotlib (comme dans astrodendro)? [Python]
Voici mon tracé résultant ci-dessous mais je voudrais qu'il ressemble aux dendrogrammes tronqués dans astrodendro:
il y a aussi un dendrogramme à l'air vraiment cool de ce document que je voudrais recréer matplotlib.
ci-Dessous est le code pour générer un iris ensemble de données avec les variables de bruit et le tracé dendrogramme matplotlib.
est-ce que quelqu'un sait comment soit: (1) tronquer les branches comme dans les figures d'exemple; et/ou (2) utiliser astrodendro avec une matrice de liaison personnalisée et des étiquettes?
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import astrodendro
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial import distance
def iris_data(noise=None, palette="hls", desat=1):
# Iris dataset
X = pd.DataFrame(load_iris().data,
index = [*map(lambda x:f"iris_{x}", range(150))],
columns = [*map(lambda x: x.split(" (cm)")[0].replace(" ","_"), load_iris().feature_names)])
y = pd.Series(load_iris().target,
index = X.index,
name = "Species")
c = map_colors(y, mode=1, palette=palette, desat=desat)#y.map(lambda x:{0:"red",1:"green",2:"blue"}[x])
if noise is not None:
X_noise = pd.DataFrame(
np.random.RandomState(0).normal(size=(X.shape[0], noise)),
index=X_iris.index,
columns=[*map(lambda x:f"noise_{x}", range(noise))]
)
X = pd.concat([X, X_noise], axis=1)
return (X, y, c)
def dism2linkage(DF_dism, method="ward"):
"""
Input: A (m x m) dissimalrity Pandas DataFrame object where the diagonal is 0
Output: Hierarchical clustering encoded as a linkage matrix
Further reading:
http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.cluster.hierarchy.linkage.html
https://pypi.python.org/pypi/fastcluster
"""
#Linkage Matrix
Ar_dist = distance.squareform(DF_dism.as_matrix())
return linkage(Ar_dist,method=method)
# Get data
X_iris_with_noise, y_iris, c_iris = iris_data(50)
# Get distance matrix
df_dism = 1- X_iris_with_noise.corr().abs()
# Get linkage matrix
Z = dism2linkage(df_dism)
#Create dendrogram
with plt.style.context("seaborn-white"):
fig, ax = plt.subplots(figsize=(13,3))
D_dendro = dendrogram(
Z,
labels=df_dism.index,
color_threshold=3.5,
count_sort = "ascending",
#link_color_func=lambda k: colors[k]
ax=ax
)
ax.set_ylabel("Distance")
1 réponses
Je ne suis pas sûr que cela constitue vraiment une réponse pratique, mais cela vous permet de générer des dendrogrammes avec des lignes pendantes tronquées. Le truc est de générer la parcelle comme d'habitude, puis de manipuler la parcelle matplotlib résultante pour recréer les lignes.
Je n'ai pas pu faire fonctionner votre exemple localement, donc je viens de créer un ensemble de données fictives.
from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
import numpy as np
a = np.random.multivariate_normal([0, 10], [[3, 1], [1, 4]], size=[5,])
b = np.random.multivariate_normal([0, 10], [[3, 1], [1, 4]], size=[5,])
X = np.concatenate((a, b),)
Z = linkage(X, 'ward')
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
dendrogram(Z, ax=ax)
la courbe résultante est le bras long habituel dendrogramme.
maintenant le plus intéressant. Un dendrogramme est composé d'un certain nombre de LineCollection objets (un pour chaque couleur). Pour mettre à jour les lignes que nous itérons à travers celles-ci, en extrayant les détails sur leurs chemins constituants, en les modifiant pour supprimer toutes les lignes atteignant un y de zéro, et ensuite recréer un LineCollection pour ces nouvelles voies.
le chemin mis à jour est alors ajouté aux axes, et le d'origine est supprimé.
la seule partie délicate est de déterminer à quelle hauteur tirer au lieu de zéro. Comme nous sommes en train d'itérer sur chaque chemin dendrogramme, nous ne savons pas quel point est venu avant - nous n'avons aucune idée de l'endroit où nous sommes. Cependant, nous pouvons exploiter le fait que les lignes suspendues pendent verticalement. S'il n'y a pas de lignes sur le même x, nous pouvons chercher les connu d'autres y valeurs pour un x et l'utiliser comme la base de notre nouvelle y lors du calcul. L'inconvénient est que, pour nous assurer d'avoir ce numéro, nous avons pré-analyser les données.
Remarque: Si vous obtenir dendrogramme de la pendaison de lignes sur le même x, vous devez inclure l' y et de recherche pour l' y le plus proche au-dessus de x pour ce faire.
import numpy as np
from matplotlib.path import Path
from matplotlib.collections import LineCollection
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
dendrogram(Z, ax=ax);
for c in ax.collections[:]: # use [:] to get a copy, since we're adding to the same list
paths = []
for path in c.get_paths():
segments = []
y_at_x = {}
# Pre-pass over all elements, to find the lowest y value at each x value.
# we can use this to caculate where to cut our lines.
for n, seg in enumerate(path.iter_segments()):
x, y = seg[0]
# Don't store if the y is zero, or if it's higher than the current low.
if y > 0 and y < y_at_x.get(x, np.inf):
y_at_x[x] = y
for n, seg in enumerate(path.iter_segments()):
x, y = seg[0]
if y == 0:
# If we know the last y at this x, use it - 0.5, limit > 0
y = max(0, y_at_x.get(x, 0) - 0.5)
segments.append([x,y])
paths.append(segments)
lc = LineCollection(paths, colors=c.get_colors()) # Recreate a LineCollection with the same params
ax.add_collection(lc)
ax.collections.remove(c) # Remove the original LineCollection
Le dendrogramme résultant ressemble à ceci: