descente en pente à l'aide de python et de numpy
def gradient(X_norm,y,theta,alpha,m,n,num_it):
temp=np.array(np.zeros_like(theta,float))
for i in range(0,num_it):
h=np.dot(X_norm,theta)
#temp[j]=theta[j]-(alpha/m)*( np.sum( (h-y)*X_norm[:,j][np.newaxis,:] ) )
temp[0]=theta[0]-(alpha/m)*(np.sum(h-y))
temp[1]=theta[1]-(alpha/m)*(np.sum((h-y)*X_norm[:,1]))
theta=temp
return theta
X_norm,mean,std=featureScale(X)
#length of X (number of rows)
m=len(X)
X_norm=np.array([np.ones(m),X_norm])
n,m=np.shape(X_norm)
num_it=1500
alpha=0.01
theta=np.zeros(n,float)[:,np.newaxis]
X_norm=X_norm.transpose()
theta=gradient(X_norm,y,theta,alpha,m,n,num_it)
print theta
Mon thêta du code ci-dessus est 100.2 100.2 , mais il devrait être 100.2 61.09 dans matlab qui est correct.
4 réponses
je pense que votre code est un peu trop compliqué et il a besoin de plus de structure, parce que sinon vous serez perdu dans toutes les équations et opérations. En fin de Compte, cette régression se résume à quatre opérations:
- calculer l'hypothèse h = X * thêta
- calculer la perte = h-y et peut - être le coût au carré (perte^2) / 2m
- Calculer le gradient = X' * perte / m
- mettre à jour les paramètres thêta = thêta-alpha * gradient
dans votre cas, je suppose que vous avez confondu m avec n . Ici m désigne le nombre d'exemples dans votre entraînement, pas le nombre de fonctionnalités.
regardons ma variation de votre code:
import numpy as np
import random
# m denotes the number of examples here, not the number of features
def gradientDescent(x, y, theta, alpha, m, numIterations):
xTrans = x.transpose()
for i in range(0, numIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y
# avg cost per example (the 2 in 2*m doesn't really matter here.
# But to be consistent with the gradient, I include it)
cost = np.sum(loss ** 2) / (2 * m)
print("Iteration %d | Cost: %f" % (i, cost))
# avg gradient per example
gradient = np.dot(xTrans, loss) / m
# update
theta = theta - alpha * gradient
return theta
def genData(numPoints, bias, variance):
x = np.zeros(shape=(numPoints, 2))
y = np.zeros(shape=numPoints)
# basically a straight line
for i in range(0, numPoints):
# bias feature
x[i][0] = 1
x[i][1] = i
# our target variable
y[i] = (i + bias) + random.uniform(0, 1) * variance
return x, y
# gen 100 points with a bias of 25 and 10 variance as a bit of noise
x, y = genData(100, 25, 10)
m, n = np.shape(x)
numIterations= 100000
alpha = 0.0005
theta = np.ones(n)
theta = gradientDescent(x, y, theta, alpha, m, numIterations)
print(theta)
d'abord, je crée un petit ensemble de données aléatoires qui devrait ressembler à ceci:
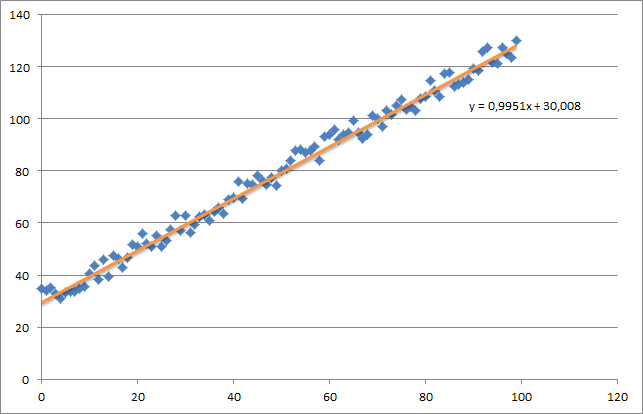
comme vous pouvez le voir, j'ai aussi ajouté la ligne de régression générée et la formule qui a été calculée par excel.
vous devez prendre soin de l'intuition de la régression en utilisant le gradient de descente. Comme vous faites un transfert de lot complet sur vos données X, vous devez réduire les pertes m de chaque exemple à une seule mise à jour de poids. Dans ce cas, c'est la moyenne de la somme des gradients, ainsi que la division par m .
le la prochaine chose dont vous devez vous soucier est de suivre la convergence et d'ajuster le taux d'apprentissage. D'ailleurs, vous devriez toujours suivre votre coût à chaque itération, peut-être même le tracer.
si vous utilisez mon exemple, la thêta retournée ressemblera à ceci:
Iteration 99997 | Cost: 47883.706462
Iteration 99998 | Cost: 47883.706462
Iteration 99999 | Cost: 47883.706462
[ 29.25567368 1.01108458]
qui est en fait assez proche de l'équation qui a été calculée par excel (y = x + 30). Notez que lorsque nous avons passé le biais dans la première colonne, la première valeur theta dénote le biais poids.
ci-dessous, vous pouvez trouver ma mise en œuvre de descente par gradient pour le problème de régression linéaire.
au début, vous calculez le gradient comme X.T * (X * w - y) / N et mettez à jour votre thêta actuel avec ce gradient simultanément.
- X: caractéristique de la matrice
- y: valeurs cibles
- w: Poids / valeurs
- N: Taille de l'ensemble de formation
voici le code python:
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import random
def generateSample(N, variance=100):
X = np.matrix(range(N)).T + 1
Y = np.matrix([random.random() * variance + i * 10 + 900 for i in range(len(X))]).T
return X, Y
def fitModel_gradient(x, y):
N = len(x)
w = np.zeros((x.shape[1], 1))
eta = 0.0001
maxIteration = 100000
for i in range(maxIteration):
error = x * w - y
gradient = x.T * error / N
w = w - eta * gradient
return w
def plotModel(x, y, w):
plt.plot(x[:,1], y, "x")
plt.plot(x[:,1], x * w, "r-")
plt.show()
def test(N, variance, modelFunction):
X, Y = generateSample(N, variance)
X = np.hstack([np.matrix(np.ones(len(X))).T, X])
w = modelFunction(X, Y)
plotModel(X, Y, w)
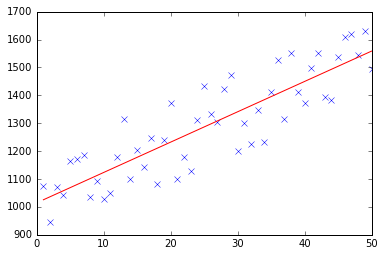
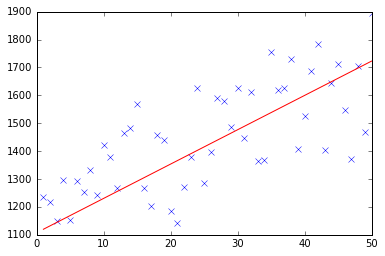
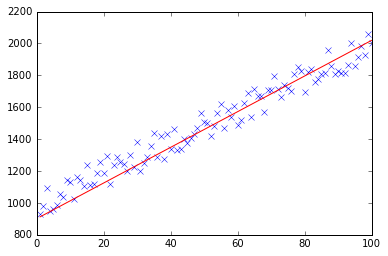
test(50, 600, fitModel_gradient)
test(50, 1000, fitModel_gradient)
test(100, 200, fitModel_gradient)
je sais que cette question a déjà été réponse mais j'ai fait une mise à jour de la fonction GD:
### COST FUNCTION
def cost(theta,X,y):
### Evaluate half MSE (Mean square error)
m = len(y)
error = np.dot(X,theta) - y
J = np.sum(error ** 2)/(2*m)
return J
cost(theta,X,y)
def GD(X,y,theta,alpha):
cost_histo = [0]
theta_histo = [0]
# an arbitrary gradient, to pass the initial while() check
delta = [np.repeat(1,len(X))]
# Initial theta
old_cost = cost(theta,X,y)
while (np.max(np.abs(delta)) > 1e-6):
error = np.dot(X,theta) - y
delta = np.dot(np.transpose(X),error)/len(y)
trial_theta = theta - alpha * delta
trial_cost = cost(trial_theta,X,y)
while (trial_cost >= old_cost):
trial_theta = (theta +trial_theta)/2
trial_cost = cost(trial_theta,X,y)
cost_histo = cost_histo + trial_cost
theta_histo = theta_histo + trial_theta
old_cost = trial_cost
theta = trial_theta
Intercept = theta[0]
Slope = theta[1]
return [Intercept,Slope]
res = GD(X,y,theta,alpha)
cette fonction réduit l'alpha au cours de l'itération ce qui fait que la fonction converge trop vite voir estimation de la régression linéaire avec Gradient de descente (descente la plus raide) pour un exemple dans R. j'applique la même logique mais en Python.
suite à l'implémentation de @thomas-jungblut en python, j'ai fait la même chose pour Octave. Si vous trouvez quelque chose qui ne va pas s'il Vous Plaît me le faire savoir et je vais corriger+mise à jour.
les données proviennent d'un fichier txt avec les lignes suivantes:
1 10 1000
2 20 2500
3 25 3500
4 40 5500
5 60 6200
pensez-y comme un échantillon très grossier pour les caractéristiques [Nombre de chambres] [mts2] et dernière colonne [Prix de location] qui est ce que nous voulons prédire.
Voici l'implémentation de L'Octave:
%
% Linear Regression with multiple variables
%
% Alpha for learning curve
alphaNum = 0.0005;
% Number of features
n = 2;
% Number of iterations for Gradient Descent algorithm
iterations = 10000
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% No need to update after here
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
DATA = load('CHANGE_WITH_DATA_FILE_PATH');
% Initial theta values
theta = ones(n + 1, 1);
% Number of training samples
m = length(DATA(:, 1));
% X with one mor column (x0 filled with '1's)
X = ones(m, 1);
for i = 1:n
X = [X, DATA(:,i)];
endfor
% Expected data must go always in the last column
y = DATA(:, n + 1)
function gradientDescent(x, y, theta, alphaNum, iterations)
iterations = [];
costs = [];
m = length(y);
for iteration = 1:10000
hypothesis = x * theta;
loss = hypothesis - y;
% J(theta)
cost = sum(loss.^2) / (2 * m);
% Save for the graphic to see if the algorithm did work
iterations = [iterations, iteration];
costs = [costs, cost];
gradient = (x' * loss) / m; % /m is for the average
theta = theta - (alphaNum * gradient);
endfor
% Show final theta values
display(theta)
% Show J(theta) graphic evolution to check it worked, tendency must be zero
plot(iterations, costs);
endfunction
% Execute gradient descent
gradientDescent(X, y, theta, alphaNum, iterations);