La différence entre un problème linéaire et non-linéaire problème? Essence de point - le produit et le noyau truc
le truc du noyau fait correspondre un problème non linéaire à un problème linéaire.
Mes questions sont:
1. Quelle est la principale différence entre un linéaire et non-linéaire problème? Quelle est l'intuition derrière la différence de ces deux classes de problèmes? Et Comment noyau astuce permet d'utiliser les classificateurs linéaires sur un problème non linéaire?
2. Pourquoi est le produit scalaire si important dans les deux cas?
Merci.
5 réponses
beaucoup de classificateurs, parmi eux le linéaire Machine à Vecteurs de Support (SVM), ne peut résoudre que des problèmes qui sont linéairement séparables, c'est-à-dire lorsque les points appartenant à la classe 1 peuvent être séparés des points appartenant à la classe 2 par un hyperplan.
dans de nombreux cas, un problème qui n'est pas linéairement séparable peut être résolu en appliquant une transformation phi() aux points de données; on dit que cette transformation transforme les points en espace. L'espoir est que, dans l'espace feature, les points seront linéairement séparables. (Note: Ce n'est pas encore le tour du noyau... restez à l'écoute.)
Il peut être démontré que, plus la dimension de l'espace de la fonctionnalité, plus le nombre de problèmes qui sont linéairement séparables dans l'espace. Donc, l'idéal serait la fonction de l'espace à dimensions que possible.
Malheureusement, comme la dimension de l'espace de la fonctionnalité augmente, la quantité de calcul nécessaire. C'est où le noyau truc. De nombreux algorithmes d'apprentissage automatique (parmi lesquels le SVM) peuvent être formulés de telle sorte que la seule opération qu'ils effectuent sur les points de données est un produit scalaire entre deux points de données. (Je vais désigner un produit scalaire entre x1 et x2 par <x1, x2>.)
si nous transformons nos points en feature space, le produit scalar ressemble maintenant à ceci:
<phi(x1), phi(x2)>
L'idée clé est que, il existe une classe de fonctions appelées les noyaux qui peut être utilisé pour optimiser le calcul de ce produit scalaire. Un noyau est une fonction K(x1, x2) qui a la propriété que
K(x1, x2) = <phi(x1), phi(x2)>
pour certaines fonctions phi (). En d'autres termes: nous pouvons évaluer le produit scalaire dans l'espace de données de faible dimension (où X1 et x2 "vivent") sans avoir à se transformer en l'espace de caractéristique de grande dimension(où phi(x1) et phi (x2) "vivent"), mais nous obtenons toujours les avantages de transformer à la de grande dimension à l'espace de la fonctionnalité. Ceci est appelé le truc du noyau.
beaucoup de noyaux populaires, comme le noyau Gaussien, correspond en fait à une Phi transform () qui se transforme en infini-dimensionnelles fonctionnalité de l'espace. Le truc du noyau nous permet de calculer des produits scalaires dans cet espace sans avoir à représenter explicitement des points dans cet espace (ce qui, évidemment, est impossible sur les ordinateurs avec des quantités limitées de mémoire).
quand les gens disent problème linéaire par rapport à un problème de classification, ils signifient généralement problème linéairement séparable. Linéairement séparable signifie qu'il existe une fonction qui permet de séparer les deux classes qui est une combinaison linéaire de la variable d'entrée. Par exemple, si vous avez deux variables d'entrée, x1 et x2, il y a quelques numéros theta1 et theta2 tels que la fonction theta1.x1 + theta2.x2 sera suffisant pour prédire la sortie. En deux dimensions correspond à une ligne droite, en 3D il devient un plan et dans les espaces dimensionnels supérieurs il devient un hyperplane.
vous pouvez obtenir une sorte d'intuition sur ces concepts en pensant à des points et des lignes en 2D/3D. Voici une paire d'exemples très astucieux...
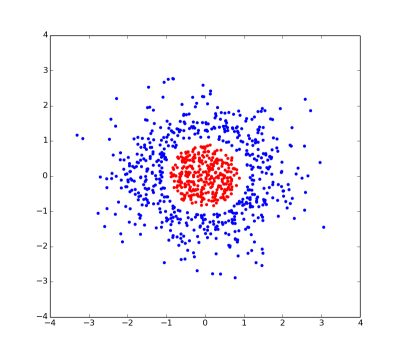
il s'agit d'une intrigue d'un problème linéairement inséparable. Il n'y a pas de ligne droite qui peut séparer le rouge et le bleu point.
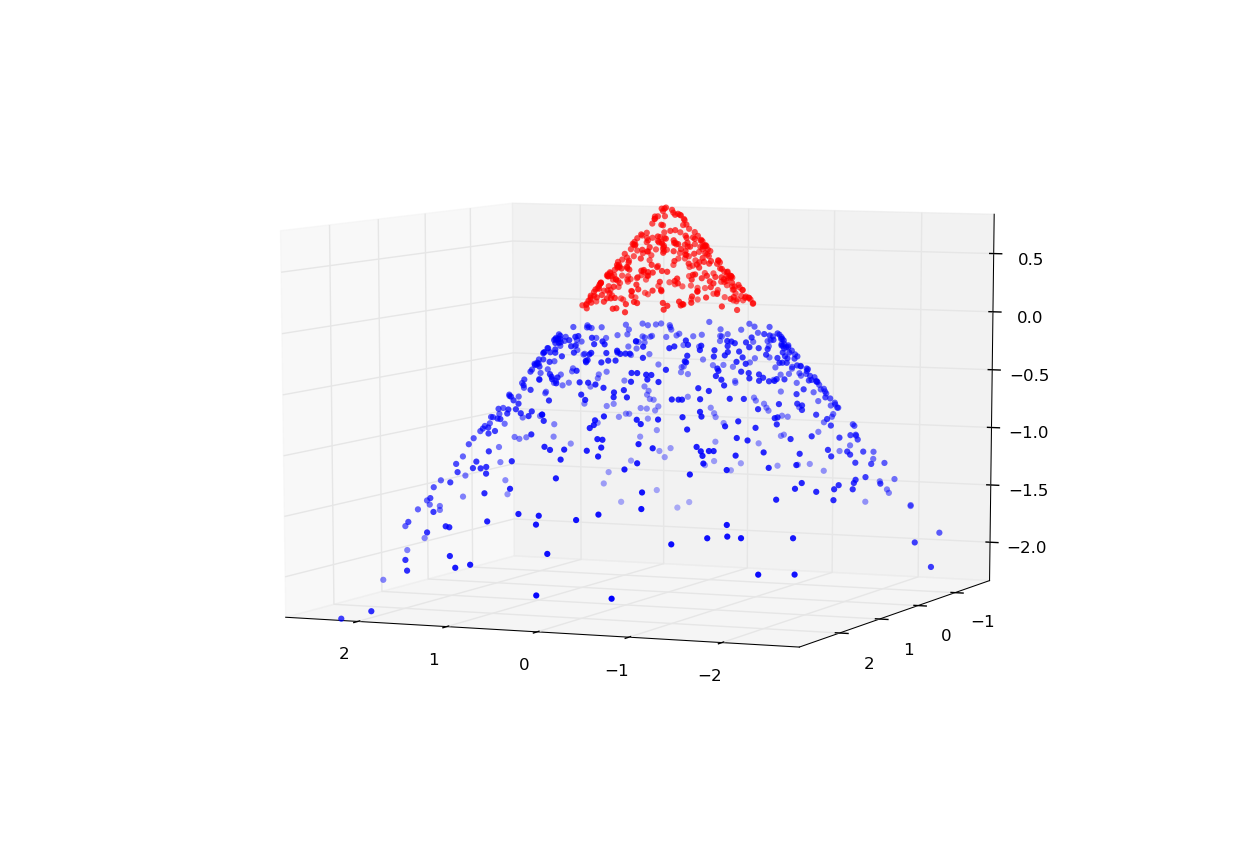
cependant, si nous donnons à chaque point une coordonnée supplémentaire (spécifiquement 1 - sqrt(x*x + y*y)... Je vous ai dit qu'il a été inventé), puis le problème devient linéairement séparable puisque les points rouges et bleus peuvent être séparés par un plan en 2 dimensions passant par z=0.
Espérons que ces exemples démontrent partie de l'idée derrière le noyau truc:
Mappage d'un problème dans un espace avec un plus grand nombre de les dimensions rendent plus probable que le problème deviendra linéairement séparable.
la deuxième idée derrière le truc du noyau (et la raison pour laquelle il est si délicat) est qu'il est généralement très difficile et coûteux de travailler dans un espace de très grande dimension. Cependant, si un algorithme utilise uniquement les produits de points entre les points (ce que vous pouvez considérer comme des distances), alors vous n'avez qu'à travailler avec une matrice de scalaires. Vous pouvez effectuer implicitement les calculs dans l'espace de dimension supérieure sans jamais avoir à faire la cartographie ou traiter les données de dimension supérieure.
la principale différence (pour des raisons pratiques) est: un problème linéaire A soit une solution (et puis il est facilement trouvé), ou vous obtenez une réponse définitive qu'il n'y a pas de solution du tout. Vous en savez autant, avant même de connaître le problème. Tant que c'est linéaire, vous obtiendrez une réponse; rapidement.
L'intuition beheind c'est le fait que si vous avez deux lignes droites dans l'espace, il est assez facile de voir si elles se croisent ou pas, et s'ils le font, c'est facile de savoir où.
si le problème n'est pas linéaire -- Eh bien, ça peut être n'importe quoi, et vous ne savez à peu près rien.
Le produit scalaire de deux vecteurs signifie simplement la suivante: La somme des produits des éléments correspondants. Donc, si votre problème est
c1 * x1 + c2 * x2 + c3 * x3 = 0
(où vous connaissez habituellement les coefficients c, et vous cherchez les variables x), le côté gauche est le produit dot des vecteurs (c1,c2,c3) et (x1,x2,x3).
ce qui précède équation est (à peu près) la définition même d'un problème linéaire, donc il ya votre lien entre le produit de points et les problèmes linéaires.
- Les équations linéaires sont homogènes, et la superposition s'applique. Vous pouvez créer des solutions en utilisant des combinaisons d'autres solutions connues; c'est l'une des raisons pour lesquelles les transformations de Fourier fonctionnent si bien. Les équations Non linéaires ne sont pas homogènes et la superposition ne s'applique pas. Les équations Non linéaires doivent généralement être résolues numériquement en utilisant des techniques itératives incrémentielles.
- Je ne sais pas comment exprimer l'importance du produit dot, mais il faut deux vecteurs et retourne un scalaire. Il est certain qu'une solution à une équation scalaire est moins efficace que la résolution d'un vecteur ou d'une équation tensorielle d'ordre supérieur, simplement parce qu'il y a moins de composants à traiter.
mon intuition dans cette affaire est plus basée sur la physique, donc j'ai du mal à traduire en AI.
je pense que lien suivant également utile ...
http://www.simafore.com/blog/bid/113227/How-support-vector-machines-use-kernel-functions-to-classify-data