Conception D'un noyau pour une machine vectorielle de soutien (XOR)

(pour quiconque n'est pas familier avec l'utilisation des fonctions du noyau dans L'apprentissage Machine, les noyaux ne font que cartographier les vecteurs d'entrée (les points de données qui composent l'ensemble de données) dans un espace plus dimensionnel, alias "L'Espace caractéristique". Le SVM trouve alors un hyperplan séparateur avec la marge maximale (distance entre l'hyperplan et les vecteurs de support) dans cet espace transformé.)

bien, commencez par les grains qui sont connus pour fonctionner avec les classificateurs SVM pour résoudre le problème de l'intérêt. Dans ce cas, nous savons que l' RBF (fonction de base radiale) noyau w/ a SVM formé, sépare proprement XOR. Vous pouvez écrire une fonction RBF en Python de cette façon:

def RBF():
    return NP.exp(-gamma * NP.abs(x - y)**2)

gamma 1/nombre de fonctionnalités (colonnes dans le jeu de données), et x, y sont Cartésien paire.

(un module de fonction de base radiale est aussi en scipy.interpoler.Rbf)

deuxièmement, si ce que vous recherchez est non seulement en utilisant les fonctions du noyau disponibles pour résoudre les problèmes de classification/régression, mais au lieu de cela vous voulez construire votre propre, je suggérerais d'abord d'étudier comment le choix de la fonction du noyau et les paramètres à l'intérieur de ces fonctions affectent les performances de classifier. Le petit groupe de fonctions du noyau couramment utilisé avec SVM / SVC est le meilleur endroit pour commencer. Ce groupe est composé de (à l'exception de RBF):

• linéaire noyau

• polynôme

• sigmoïde

mon approche serait d'étudier les données: Comment séparer les points du problème XOR? Quand j'ai commencé à étudier sur M. L. en général, et SVM en particulier, c'est ce que j'ai fait, a pris problème de jouet, le dessiner à la main, et essayer de séparer les classes.

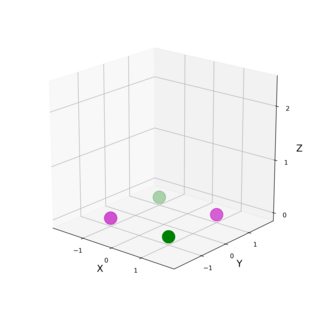
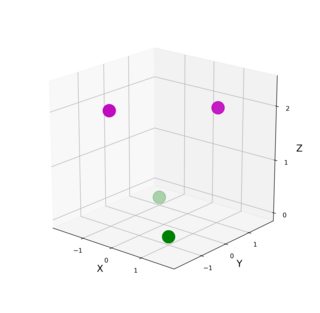
quand j'ai regardé le problème de XOR la première fois, il m'est venu à l'esprit que les deux points pourpres (ci-dessous, à gauche) ont X et Y du même signe, dans un cas négatif dans un positif, alors que les deux points verts ont X et Y de des signes opposés. Par conséquent, la somme au carré de X et Y serait 0 (ou très petit avec un peu de bruit dans le problème initial) pour les points verts, et 2 (ou presque 2) pour les violets. Par conséquent, ajouter une troisième coordonnée Z = np.sqrt(np.square(X + Y)) faudra bien séparer les deux séries:

Sur une note de côté, Z n'est pas trop différent de la formulation de le rbf de doug si vous considérez que np.sqrt(np.square(X + Y)) est essentiellement identique à np.abs(X + Y) dans ce cas.

Je n'ai pas accès au papier de Crisitanini mais j'aborderais ce problème aussi d'une manière similaire, en commençant par une version jouet (soit dit en passant, code de damier merci à rien d'autre qu' doug):

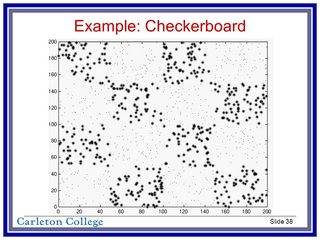
une intuition possible ici est que la somme des indices de ligne et de colonne pour les carrés noirs serait toujours égale, alors que pour les les carrés blancs seraient toujours étranges, donc en ajoutant comme troisième dimension quelque chose comme (row_index + col_index) % 2 ferait l'affaire dans cette version simple. Dans un ensemble de données de damier plus grand et plus complexe, comme celui-ci que j'ai trouvé sur le web:

les choses ne sont pas si simples, mais peut-être pourrait-on faire une cascade de clusters pour trouver les emplacements X et Y moyens des 16 clusters (peut-être en utilisant medoids de clustering), puis appliquer une version du " modulo kernel trick"?

Avec l'avertissement que je n'ai pas travaillé avec une tonne de problèmes de classification, pour l'instant j'ai trouvé qu'en faisant un jouet version de complexe, habituellement, j'ai acquis une 'numérique' intuition pour le type de solution qui pourrait fonctionner.

enfin, comme indiqué dans un commentaire à la réponse de doug, Je ne trouve rien de mal à un approche empirique comme sa, étudiant la performance de tous les noyaux possibles en les passant à la grille rechercher dans la validation croisée imbriquée avec le même algorithme (SVC) et changer seulement le noyau. Vous pouvez ajouter à cette approche en traçant les marges respectives dans les espaces transformés: par exemple, pour rbf, en utilisant l'équation suggérée par Doug (et Sebastian Raschka la routine de traquer les régions de décision - cellule 13 ici).

mise à jour 27/17 octobre Dans une conversation sur mon canal mou, un autre géophysicien m'a questionné sur le cas que la porte XOR est conçue comme 0s et 1s par opposition à-1s et 1s (ce dernier étant similaire à un problème classique en géophysique d'exploration, d'où mon premier exemple de jouet).

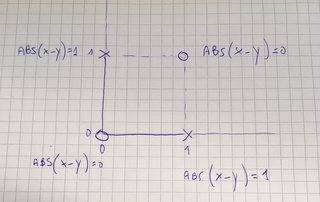
si je m'attaquais à la porte XOR avec des 0 et des 1, et que je n'avais pas la connaissance du noyau rbf, dans ce cas aussi je m'asseyais et je regardais le problème en termes de coordonnées de ces problèmes et je voyais si je pouvais arriver à une transformation.

ma première observation ici était que les Os sont assis sur le x=y ligne, le Xs sur l' x=-y ligne, de sorte que la différence x-y 0 (ou petit, avec un peu de bruit) dans un cas, +/-1 dans l'autre, respectivement. La valeur absolue prendrait soin du signe, donc Z = np.abs(X-Y) va fonctionner. Qui, en passant, est très similaire à doug estrbf = np.exp(-gamma * np.abs(x - y)**2) (une autre raison d'augmenter sa réponse); et en fait, sa rbf est solution plus générale, travaillant dans tous les cas XOR.

je suis à la recherche d'un travail de noyau polynomial à travers des exemples et je suis tombé sur ce post. Un couple de choses qui pourraient aider si vous êtes toujours à la recherche sont cette boîte à outils (http://www2.fml.tuebingen.mpg.de/raetsch/projects/shogun) qui utilise l'apprentissage du noyau multiple, où vous pouvez choisir une large sélection de méthodes du noyau et ensuite l'apprentissage choisira le meilleur pour le problème, donc vous n'avez pas à le faire.

une méthode plus simple et plus traditionnelle pour votre choix de noyau est d'utiliser validation croisée avec différentes méthodes de noyau pour trouver le meilleur.

J'espère que cela vous aidera, vous ou quelqu'un d'autre, à lire autour des méthodes du noyau.