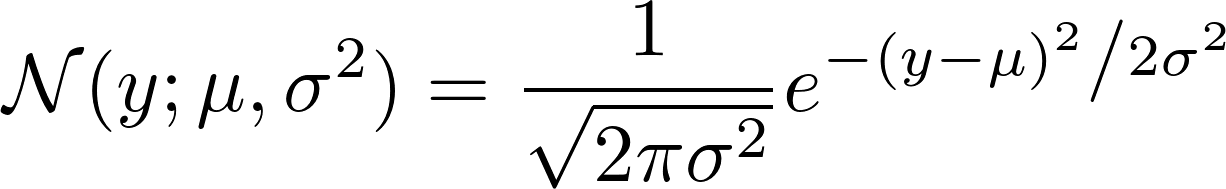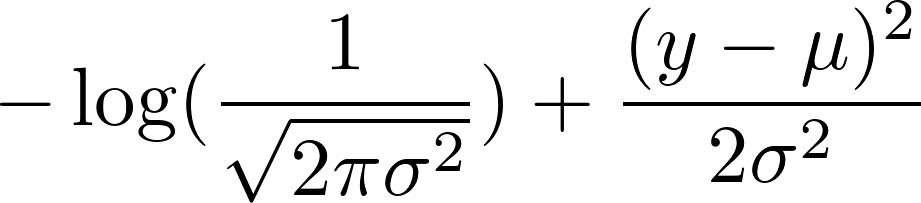Fonction de coût pour la régression logistique
dans les modèles des moindres carrés, la fonction de coût est définie comme le carré de la différence entre la valeur prévue et la valeur réelle en fonction de l'intrant.
quand nous faisons une régression logistique, nous changeons la fonction de coût pour une fonction logirithmique, au lieu de la définir comme étant le carré de la différence entre la fonction sigmoïde (la valeur de sortie) et la sortie réelle.
est-il correct de changer et de définir notre propre fonction de coût pour déterminer les paramètres?
4 réponses
Oui, vous définissez votre propre fonction de perte, mais si vous êtes un novice, vous êtes probablement mieux en utilisant un de la littérature. Il y a des conditions que les fonctions de perte doivent remplir:
ils devraient se rapprocher de la perte réelle que vous essayez de minimiser. Comme il a été dit dans l'autre réponse, les fonctions de perte standard pour la classification est zéro-une perte (taux de classification erronée) et ceux utilisés pour les classificateurs de formation sont des approximations de ce qui suit: perte.
la perte d'erreur quadratique de la régression linéaire n'est pas utilisée parce qu'elle n'est pas approximative de zéro-une-perte bien: lorsque votre modèle prédit +50 pour un échantillon alors que la réponse prévue était +1 (classe positive), la prédiction est du bon côté de la limite de décision donc la perte zéro-une est zéro, mais la perte d'erreur quadratique est toujours 492 = 2401. Certains algorithmes de formation va perdre beaucoup de temps à obtenir des prédictions très proche de {-1, +1} au lieu de se concentrer sur l'obtention juste le signe/classe étiquette de droite.(*)
la fonction de perte devrait fonctionner avec votre algorithme d'optimisation prévu. C'est pourquoi zero-one-loss n'est pas utilisé directement: il ne fonctionne pas avec les méthodes d'optimisation basées sur le gradient car il n'a pas de gradient bien défini (ou même un subgradient, comme la perte de charnière pour SVMs a).
l'algorithme principal qui optimise directement la perte zéro-un est le vieux perceptron algorithme.
en outre, lorsque vous branchez une fonction de perte personnalisée, vous ne construisez plus un modèle de régression logistique, mais une autre sorte de classificateur linéaire.
(*) erreur au carré utilisé avec l'analyse discriminante linéaire, mais qui est généralement résolu sous forme proche au lieu de itérativement.
la fonction logistique, la perte de la charnière, la perte de la charnière lissée,etc. sont utilisés parce qu'ils sont des limites supérieures sur la perte de classification binaire zéro-un.
ces fonctions pénalisent aussi généralement les exemples qui sont correctement classés mais qui sont encore près de la limite de décision, créant ainsi une "marge"."
donc, si vous faites une classification binaire, alors vous devriez certainement choisir une fonction de perte standard.
Si vous essayez de résoudre un autre problème, une perte de la fonction fera mieux.
vous ne choisissez pas la fonction de perte, vous choisissez le modèle
la fonction de perte est habituellement déterminée directement par le modèle lorsque vous ajustez vos paramètres en utilisant L'Estimation de vraisemblance maximale (MLE), qui est l'approche la plus populaire dans L'apprentissage automatique.
vous avez mentionné L'erreur quadratique moyenne comme fonction de perte pour la régression linéaire. Puis "nous changeons la fonction de coût en fonction logarithmique", se référant à la perte entropique croisée. Nous n'avons pas à changer la la fonction de coût. En fait, L'erreur quadratique moyenne est la perte D'entropie croisée pour la régression linéaire, lorsque nous supposons yà distribuer normalement par un gaussien, dont la moyenne est définie par Wx + b.
Explication
avec MLE, vous choisissez les paramètres de manière à maximiser la probabilité des données de formation. La probabilité de l'ensemble des données sur la formation est un produit des probabilités de chaque échantillon de formation. Parce que cela peut couler à zéro, nous avons habituellement maximiser la probabilité logarithmique des données de formation / minimiser la probabilité logarithmique négative. Ainsi, la fonction de coût devient une somme de la log-probabilité négative de chaque échantillon de formation, qui est donnée par:
-log(p(y | x; w))
où w sont les paramètres de notre modèle (y compris la polarisation). Maintenant, pour la régression logistique, c'est le logarithme auquel vous avez fait référence. Mais qu'en est-il de l'affirmation, que cela correspond également à la MSE pour linéaire une régression?
Exemple
Pour afficher le MSE correspond à l'entropie croisée, nous supposons que y est normalement distribué autour d'une moyenne, que nous prédisons en utilisant w^T x + b. Nous supposons aussi qu'il a une variance fixe, donc nous ne prédisons pas la variance avec notre régression linéaire, seulement la moyenne du gaussien.
p(y | x; w) = N(y; w^T x + b, 1)
Vous pouvez le voir, mean = w^T x + b et variance = 1
maintenant, la fonction de perte correspond
-log N(y; w^T x + b, 1)
si nous regardons comment le gaussien N est défini, nous voir:
maintenant, prenez le logarithme négatif de cela. Il en résulte:
nous avons choisi une variance fixe de 1. Cela rend le premier terme constant et réduit le second terme à:
0.5 (y - mean)^2
Maintenant, rappelez-vous que nous défini la moyenne comme w^T x + b. Puisque le premier terme est constant, minimiser le logarithme négatif du gaussien correspond à minimiser
(y - w^T x + b)^2
ce qui correspond à minimiser l'erreur quadratique moyenne.
Oui, d'autres fonctions de coût peut être utilisé pour déterminer les paramètres.
la fonction d'erreur au Carré (Fonction couramment utilisée pour la régression linéaire) ne convient pas très bien à la régression logistique.
comme dans le cas de la régression logistique, l'hypothèse est non linéaire (fonction sigmoïde), ce qui fait que la fonction d'erreur carrée est non convexe.
La fonction logarithme est une fonction convexe qui n'est pas local optima, donc la descente en pente fonctionne bien.