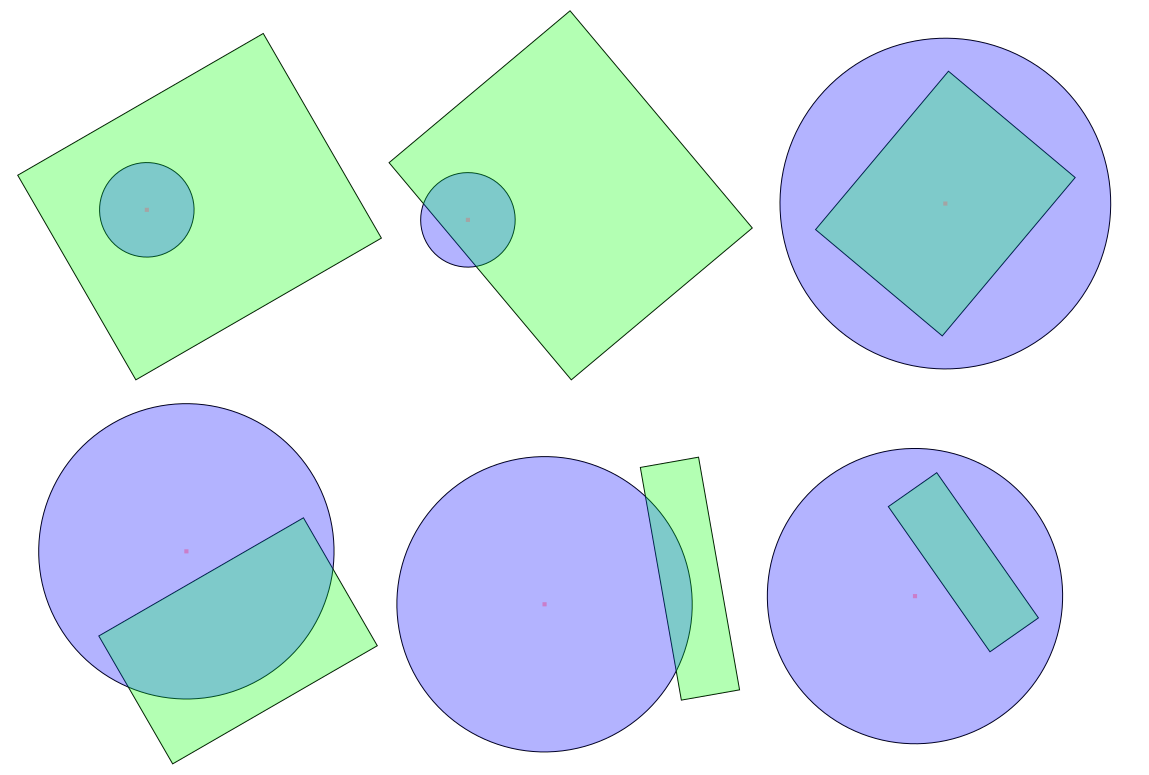
Détection des collisions cercle-Rectangle (intersection)

Voici comment je le ferais:

bool intersects(CircleType circle, RectType rect)
{
    circleDistance.x = abs(circle.x - rect.x);
    circleDistance.y = abs(circle.y - rect.y);

    if (circleDistance.x > (rect.width/2 + circle.r)) { return false; }
    if (circleDistance.y > (rect.height/2 + circle.r)) { return false; }

    if (circleDistance.x <= (rect.width/2)) { return true; } 
    if (circleDistance.y <= (rect.height/2)) { return true; }

    cornerDistance_sq = (circleDistance.x - rect.width/2)^2 +
                         (circleDistance.y - rect.height/2)^2;

    return (cornerDistance_sq <= (circle.r^2));
}

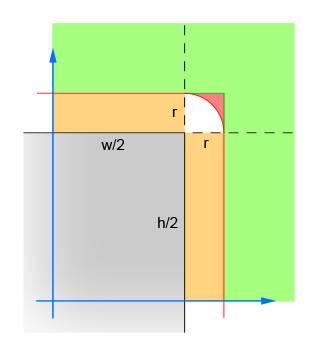
Voici comment ça marche:

1. la première paire de lignes calcule les valeurs absolues de la différence de x et de y entre le centre du cercle et le centre du rectangle. Cela réduit les quatre quadrants en un, de sorte que les calculs ne doivent pas être faits quatre fois. L'image montre la zone dans que le centre du cercle doit maintenant se trouver. Notez que seul le quadrant est indiqué. Le rectangle est la zone grise, et la bordure rouge délimite la zone critique qui est exactement à un rayon des bords du rectangle. Le centre du cercle est à l'intérieur de cette bordure rouge pour l'intersection de se produire.

2. la deuxième paire de lignes élimine les cas faciles où le cercle est assez éloigné du rectangle (dans l'un ou l'autre direction) qu'aucune intersection n'est possible. Cela correspond à la zone verte dans l'image.

3. la troisième paire de lignes gère les cas faciles où le cercle est assez proche du rectangle (dans l'une ou l'autre direction) qu'une intersection est garantie. Cela correspond aux sections orange et grise de l'image. Notez que cette étape doit être effectuée après l'étape 2 de la logique du sens.

4. le les lignes restantes calculent le cas difficile où le cercle peut croiser le coin du rectangle. Pour résoudre, de calculer la distance à partir du centre du cercle et l'angle, puis vérifiez que la distance n'est pas plus que le rayon du cercle. Ce calcul retourne false pour tous les cercles dont le centre est à l'intérieur de la zone ombrée rouge et retourne true pour tous les cercles dont le centre est à l'intérieur de la zone ombrée blanche.

Voici une autre solution qui est assez simple à mettre en œuvre (et assez rapide, aussi). Il saisira toutes les intersections, y compris lorsque la sphère est entièrement entrée dans le rectangle.

// clamp(value, min, max) - limits value to the range min..max

// Find the closest point to the circle within the rectangle
float closestX = clamp(circle.X, rectangle.Left, rectangle.Right);
float closestY = clamp(circle.Y, rectangle.Top, rectangle.Bottom);

// Calculate the distance between the circle's center and this closest point
float distanceX = circle.X - closestX;
float distanceY = circle.Y - closestY;

// If the distance is less than the circle's radius, an intersection occurs
float distanceSquared = (distanceX * distanceX) + (distanceY * distanceY);
return distanceSquared < (circle.Radius * circle.Radius);

avec n'importe quelle bibliothèque de maths décente, qui peut être raccourcie à 3 ou 4 lignes.

votre sphère et rect se croisent IIF

la distance entre le centre du cercle et un sommet de votre rect est plus petite que le rayon de votre sphère

Ou

la distance entre le centre du cercle et un bord de votre rect est plus petite que le rayon de votre sphère ([ point-line distance ])

Ou

le centre du cercle est à l'intérieur du rect



distance point - point:

P1 = [x1,y1]
P2 = [x2,y2]
Distance = sqrt(abs(x1 - x2)+abs(y1-y2))

point-ligne distance:

L1 = [x1,y1],L2 = [x2,y2] (two points of your line, ie the vertex points)
P1 = [px,py] some point

Distance d =  abs( (x2-x1)(y1-py)-(x1-px)(y2-y1) ) / Distance(L1,L2)

cercle de centre à l'intérieur de rect:

prendre un axe de séparation aproach: s'il existe une projection sur une ligne qui sépare le rectangle du point, ils ne se croisent pas

vous projetez le point sur des lignes parallèles aux côtés de votre fond et peut alors déterminer si elles se croisent. s'ils ne se croisent pas sur les 4 projections, ils (le point et le rectangle) ne peuvent pas se croiser.

vous avez juste besoin du produit intérieur (x= [x1,x2] , y = [y1,y2] , x*y = x1*y1 + x2*y2 )

votre test ressemblerait à cela:

//rectangle edges: TL (top left), TR (top right), BL (bottom left), BR (bottom right)
//point to test: POI

seperated = false
for egde in { {TL,TR}, {BL,BR}, {TL,BL},{TR-BR} }:  // the edges
    D = edge[0] - edge[1]
    innerProd =  D * POI
    Interval_min = min(D*edge[0],D*edge[1])
    Interval_max = max(D*edge[0],D*edge[1])
    if not (  Interval_min ≤ innerProd ≤  Interval_max ) 
           seperated = true
           break  // end for loop 
    end if
end for
if (seperated is true)    
      return "no intersection"
else 
      return "intersection"
end if

ceci ne suppose pas un rectangle aligné sur l'axe et est facilement extensible pour tester les intersections entre ensembles convexes.

C'est la solution la plus rapide:

public static boolean intersect(Rectangle r, Circle c)
{
    float cx = Math.abs(c.x - r.x - r.halfWidth);
    float xDist = r.halfWidth + c.radius;
    if (cx > xDist)
        return false;
    float cy = Math.abs(c.y - r.y - r.halfHeight);
    float yDist = r.halfHeight + c.radius;
    if (cy > yDist)
        return false;
    if (cx <= r.halfWidth || cy <= r.halfHeight)
        return true;
    float xCornerDist = cx - r.halfWidth;
    float yCornerDist = cy - r.halfHeight;
    float xCornerDistSq = xCornerDist * xCornerDist;
    float yCornerDistSq = yCornerDist * yCornerDist;
    float maxCornerDistSq = c.radius * c.radius;
    return xCornerDistSq + yCornerDistSq <= maxCornerDistSq;
}

noter l'ordre d'exécution, et la moitié de la largeur/hauteur est pré-calculée. Aussi la quadrature est faite "manuellement" pour sauver quelques cycles d'horloge.

en Fait, c'est beaucoup plus simple. Vous avez seulement besoin de deux choses.

vous devez D'abord trouver quatre distances orthogonales entre le centre du cercle et chaque ligne du rectangle. Alors votre cercle ne coupera pas le rectangle si trois d'entre eux sont plus grands que le rayon du cercle.

Deuxièmement, vous devez trouver la distance entre le centre du cercle et le centre du rectangle, alors vous cercle ne sera pas à l'intérieur de la rectangle si la distance est supérieure à la moitié de la longueur diagonale du rectangle.

bonne chance!

voici mon code C pour résoudre une collision entre une sphère et une boîte non alignée. Il s'appuie sur quelques-unes de mes propres routines de bibliothèque, mais il peut s'avérer utile pour certains. Je l'utilise dans un jeu et il fonctionne parfaitement.

float physicsProcessCollisionBetweenSelfAndActorRect(SPhysics *self, SPhysics *actor)
{
    float diff = 99999;

    SVector relative_position_of_circle = getDifference2DBetweenVectors(&self->worldPosition, &actor->worldPosition);
    rotateVector2DBy(&relative_position_of_circle, -actor->axis.angleZ); // This aligns the coord system so the rect becomes an AABB

    float x_clamped_within_rectangle = relative_position_of_circle.x;
    float y_clamped_within_rectangle = relative_position_of_circle.y;
    LIMIT(x_clamped_within_rectangle, actor->physicsRect.l, actor->physicsRect.r);
    LIMIT(y_clamped_within_rectangle, actor->physicsRect.b, actor->physicsRect.t);

    // Calculate the distance between the circle's center and this closest point
    float distance_to_nearest_edge_x = relative_position_of_circle.x - x_clamped_within_rectangle;
    float distance_to_nearest_edge_y = relative_position_of_circle.y - y_clamped_within_rectangle;

    // If the distance is less than the circle's radius, an intersection occurs
    float distance_sq_x = SQUARE(distance_to_nearest_edge_x);
    float distance_sq_y = SQUARE(distance_to_nearest_edge_y);
    float radius_sq = SQUARE(self->physicsRadius);
    if(distance_sq_x + distance_sq_y < radius_sq)   
    {
        float half_rect_w = (actor->physicsRect.r - actor->physicsRect.l) * 0.5f;
        float half_rect_h = (actor->physicsRect.t - actor->physicsRect.b) * 0.5f;

        CREATE_VECTOR(push_vector);         

        // If we're at one of the corners of this object, treat this as a circular/circular collision
        if(fabs(relative_position_of_circle.x) > half_rect_w && fabs(relative_position_of_circle.y) > half_rect_h)
        {
            SVector edges;
            if(relative_position_of_circle.x > 0) edges.x = half_rect_w; else edges.x = -half_rect_w;
            if(relative_position_of_circle.y > 0) edges.y = half_rect_h; else edges.y = -half_rect_h;   

            push_vector = relative_position_of_circle;
            moveVectorByInverseVector2D(&push_vector, &edges);

            // We now have the vector from the corner of the rect to the point.
            float delta_length = getVector2DMagnitude(&push_vector);
            float diff = self->physicsRadius - delta_length; // Find out how far away we are from our ideal distance

            // Normalise the vector
            push_vector.x /= delta_length;
            push_vector.y /= delta_length;
            scaleVector2DBy(&push_vector, diff); // Now multiply it by the difference
            push_vector.z = 0;
        }
        else // Nope - just bouncing against one of the edges
        {
            if(relative_position_of_circle.x > 0) // Ball is to the right
                push_vector.x = (half_rect_w + self->physicsRadius) - relative_position_of_circle.x;
            else
                push_vector.x = -((half_rect_w + self->physicsRadius) + relative_position_of_circle.x);

            if(relative_position_of_circle.y > 0) // Ball is above
                push_vector.y = (half_rect_h + self->physicsRadius) - relative_position_of_circle.y;
            else
                push_vector.y = -((half_rect_h + self->physicsRadius) + relative_position_of_circle.y);

            if(fabs(push_vector.x) < fabs(push_vector.y))
                push_vector.y = 0;
            else
                push_vector.x = 0;
        }

        diff = 0; // Cheat, since we don't do anything with the value anyway
        rotateVector2DBy(&push_vector, actor->axis.angleZ);
        SVector *from = &self->worldPosition;       
        moveVectorBy2D(from, push_vector.x, push_vector.y);
    }   
    return diff;
}

pour visualiser, prenez la tête de votre clavier. Si la touche " 5 " représente votre rectangle, alors toutes les touches 1-9 représentent les 9 quadrants d'espace divisés par les lignes qui composent votre rectangle (avec 5 étant l'intérieur.)

1) si le centre du cercle se trouve dans le quadrant 5 (c.-à-d. à l'intérieur du rectangle), les deux formes se croisent.

avec cela hors du chemin, il y a deux cas possibles: a) le cercle se croise avec deux ou plusieurs voisins les bords du rectangle. b) Le cercle croise un bord du rectangle.

le premier cas est simple. Si le cercle coupe avec deux voisins bords du rectangle, il doit contenir le coin reliant ces deux bords. (Cela, ou son centre se trouve dans le quadrant 5, que nous avons déjà couvert. Notez également que le cas où le cercle se croise avec seulement deux s'opposant aux bords du rectangle est également couvert.)

2) si l'un des Coins A, B, C, D du rectangle se trouve à l'intérieur du cercle, alors les deux formes se croisent.

Le deuxième cas est plus délicat. Il faut noter que cela ne peut se produire que lorsque le centre du cercle se trouve dans l'un des quadrants 2, 4, 6 ou 8. (En fait, si le centre est sur l'un des quadrants 1, 3, 7, 8, le coin correspondant sera le point le plus proche de lui.)

Maintenant, nous avons le cas que le centre du cercle est dans l'un des les quadrants 'bord', et ils ne croisent que le bord correspondant. Puis, le point sur le bord le plus proche du centre du cercle, doit se trouver à l'intérieur du cercle.

3) pour chaque ligne AB, BC, CD, DA, construire les lignes perpendiculaires p(AB,P), p(BC,P), p(CD,P), p(DA,P) à travers le centre du cercle P. pour chaque ligne perpendiculaire, si l'intersection avec le bord d'origine se trouve à l'intérieur du cercle, alors les deux formes se croisent.

il y a un raccourci pour cette dernière étape. Si le centre du cercle est dans le quadrant 8 et que le bord AB est le bord supérieur, le point d'intersection aura la coordonnée y DE A et B, et la coordonnée x du Centre P.

vous pouvez construire les quatre intersections de ligne et vérifier si elles se trouvent sur leurs bords correspondants, ou trouver quel quadrant P est dedans et vérifier l'intersection correspondante. Les deux devraient simplifier la même équation booléenne. Méfiez-vous de l'étape 2 ci-dessus n'a pas exclure P étant dans l'un des quadrants de "coin"; il a juste cherché une intersection.

Edit: comme il s'avère, j'ai négligé le simple fait que #2 est un sous-cas de #3 ci-dessus. Après tout, les coins aussi sont des points sur les bords. Voir la réponse de @ShreevatsaR ci-dessous pour une excellente explication. Et en attendant, oubliez le numéro 2 ci-dessus à moins que vous ne vouliez une vérification rapide mais redondante.

cette fonction détecte les collisions (intersections) entre le cercle et le Rectangle. Il travaille comme E. Méthode James dans sa réponse, mais celle-ci détecte les collisions pour tous les angles du rectangle (pas seulement à droite en haut du coin).

NOTE:

aRect.origine.x et aRect.origine.y sont les coordonnées de l'angle inférieur gauche du rectangle!

acrcle.x et acrcle.y sont les coordonnées du Centre du cercle!

static inline BOOL RectIntersectsCircle(CGRect aRect, Circle aCircle) {

    float testX = aCircle.x;
    float testY = aCircle.y;

    if (testX < aRect.origin.x)
        testX = aRect.origin.x;
    if (testX > (aRect.origin.x + aRect.size.width))
        testX = (aRect.origin.x + aRect.size.width);
    if (testY < aRect.origin.y)
        testY = aRect.origin.y;
    if (testY > (aRect.origin.y + aRect.size.height))
        testY = (aRect.origin.y + aRect.size.height);

    return ((aCircle.x - testX) * (aCircle.x - testX) + (aCircle.y - testY) * (aCircle.y - testY)) < aCircle.radius * aCircle.radius;
}

la solution la plus simple que j'ai trouvée est assez simple.

il fonctionne en trouvant le point dans le rectangle le plus proche du cercle, puis en comparant la distance.

vous pouvez faire tout cela avec quelques opérations, et même éviter la fonction sqrt.

public boolean intersects(float cx, float cy, float radius, float left, float top, float right, float bottom)
{
   float closestX = (cx < left ? left : (cx > right ? right : cx));
   float closestY = (cy < top ? top : (cy > bottom ? bottom : cy));
   float dx = closestX - cx;
   float dy = closestY - cy;

   return ( dx * dx + dy * dy ) <= radius * radius;
}

Et c'est tout! La solution ci-dessus suppose une origine dans la partie supérieure gauche du monde avec l'axe des abscisses pointant vers le bas.

Si vous voulez une solution pour gérer les collisions entre un cercle mobile et un rectangle, c'est beaucoup plus compliqué et couvert dans une autre de mes réponses.

j'ai créé la classe pour le travail avec des formes espérons que vous apprécierez

public class Geomethry {
  public static boolean intersectionCircleAndRectangle(int circleX, int circleY, int circleR, int rectangleX, int rectangleY, int rectangleWidth, int rectangleHeight){
    boolean result = false;

    float rectHalfWidth = rectangleWidth/2.0f;
    float rectHalfHeight = rectangleHeight/2.0f;

    float rectCenterX = rectangleX + rectHalfWidth;
    float rectCenterY = rectangleY + rectHalfHeight;

    float deltax = Math.abs(rectCenterX - circleX);
    float deltay = Math.abs(rectCenterY - circleY);

    float lengthHypotenuseSqure = deltax*deltax + deltay*deltay;

    do{
        // check that distance between the centerse is more than the distance between the circumcircle of rectangle and circle
        if(lengthHypotenuseSqure > ((rectHalfWidth+circleR)*(rectHalfWidth+circleR) + (rectHalfHeight+circleR)*(rectHalfHeight+circleR))){
            //System.out.println("distance between the centerse is more than the distance between the circumcircle of rectangle and circle");
            break;
        }

        // check that distance between the centerse is less than the distance between the inscribed circle
        float rectMinHalfSide = Math.min(rectHalfWidth, rectHalfHeight);
        if(lengthHypotenuseSqure < ((rectMinHalfSide+circleR)*(rectMinHalfSide+circleR))){
            //System.out.println("distance between the centerse is less than the distance between the inscribed circle");
            result=true;
            break;
        }

        // check that the squares relate to angles
        if((deltax > (rectHalfWidth+circleR)*0.9) && (deltay > (rectHalfHeight+circleR)*0.9)){
            //System.out.println("squares relate to angles");
            result=true;
        }
    }while(false);

    return result;
}

public static boolean intersectionRectangleAndRectangle(int rectangleX, int rectangleY, int rectangleWidth, int rectangleHeight, int rectangleX2, int rectangleY2, int rectangleWidth2, int rectangleHeight2){
    boolean result = false;

    float rectHalfWidth = rectangleWidth/2.0f;
    float rectHalfHeight = rectangleHeight/2.0f;
    float rectHalfWidth2 = rectangleWidth2/2.0f;
    float rectHalfHeight2 = rectangleHeight2/2.0f;

    float deltax = Math.abs((rectangleX + rectHalfWidth) - (rectangleX2 + rectHalfWidth2));
    float deltay = Math.abs((rectangleY + rectHalfHeight) - (rectangleY2 + rectHalfHeight2));

    float lengthHypotenuseSqure = deltax*deltax + deltay*deltay;

    do{
        // check that distance between the centerse is more than the distance between the circumcircle
        if(lengthHypotenuseSqure > ((rectHalfWidth+rectHalfWidth2)*(rectHalfWidth+rectHalfWidth2) + (rectHalfHeight+rectHalfHeight2)*(rectHalfHeight+rectHalfHeight2))){
            //System.out.println("distance between the centerse is more than the distance between the circumcircle");
            break;
        }

        // check that distance between the centerse is less than the distance between the inscribed circle
        float rectMinHalfSide = Math.min(rectHalfWidth, rectHalfHeight);
        float rectMinHalfSide2 = Math.min(rectHalfWidth2, rectHalfHeight2);
        if(lengthHypotenuseSqure < ((rectMinHalfSide+rectMinHalfSide2)*(rectMinHalfSide+rectMinHalfSide2))){
            //System.out.println("distance between the centerse is less than the distance between the inscribed circle");
            result=true;
            break;
        }

        // check that the squares relate to angles
        if((deltax > (rectHalfWidth+rectHalfWidth2)*0.9) && (deltay > (rectHalfHeight+rectHalfHeight2)*0.9)){
            //System.out.println("squares relate to angles");
            result=true;
        }
    }while(false);

    return result;
  } 
}

voici le code modelé 100% working:

public static bool IsIntersected(PointF circle, float radius, RectangleF rectangle)
{
    var rectangleCenter = new PointF((rectangle.X +  rectangle.Width / 2),
                                     (rectangle.Y + rectangle.Height / 2));

    var w = rectangle.Width  / 2;
    var h = rectangle.Height / 2;

    var dx = Math.Abs(circle.X - rectangleCenter.X);
    var dy = Math.Abs(circle.Y - rectangleCenter.Y);

    if (dx > (radius + w) || dy > (radius + h)) return false;

    var circleDistance = new PointF
                             {
                                 X = Math.Abs(circle.X - rectangle.X - w),
                                 Y = Math.Abs(circle.Y - rectangle.Y - h)
                             };

    if (circleDistance.X <= (w))
    {
        return true;
    }

    if (circleDistance.Y <= (h))
    {
        return true;
    }

    var cornerDistanceSq = Math.Pow(circleDistance.X - w, 2) + 
                                    Math.Pow(circleDistance.Y - h, 2);

    return (cornerDistanceSq <= (Math.Pow(radius, 2)));
}

Bassam Alugili

voici un test rapide d'une ligne pour cela:

if (length(max(abs(center - rect_mid) - rect_halves, 0)) <= radius ) {
  // They intersect.
}

c'est le cas aligné sur l'axe où rect_halves est un vecteur positif pointant du milieu du rectangle vers un coin. L'expression à l'intérieur de length() est un vecteur delta allant de center à un point le plus proche dans le rectangle. Cela fonctionne dans n'importe quelle dimension.

• vérifier D'abord si le rectangle et la tangente carrée au cercle se chevauchent (facile). S'ils ne se chevauchent pas, ils ne se heurtent pas.
• vérifiez si le centre du cercle est à l'intérieur du rectangle (facile). Si c'est à l'intérieur, ils entrent en collision.
• Calculez la distance carrée minimale entre les côtés du rectangle et le centre du cercle (petit dur). S'il est plus bas que le rayon carré, alors ils entrent en collision, sinon ils ne le font pas.

c'est efficace, parce que:

• tout d'abord, il vérifie le scénario le plus commun avec un algorithme bon marché et quand il est sûr qu'ils ne se heurtent pas, il se termine.
• ensuite, il vérifie le scénario le plus commun suivant avec un algorithme bon marché (ne calculez pas la racine carrée, utilisez les valeurs carrées) et quand il est sûr qu'ils entrent en collision, il se termine.
• exécute alors l'algorithme le plus coûteux pour vérifier la collision avec le rectangle frontières.

j'ai une méthode qui évite de coûteux pythagore si pas nécessaire - ie. quand les boîtes du rectangle et du cercle ne se croisent pas.

et ça marchera aussi pour les non-euclidiens:

class Circle {
 // create the bounding box of the circle only once
 BBox bbox;

 public boolean intersect(BBox b) {
    // test top intersect
    if (lat > b.maxLat) {
        if (lon < b.minLon)
            return normDist(b.maxLat, b.minLon) <= normedDist;
        if (lon > b.maxLon)
            return normDist(b.maxLat, b.maxLon) <= normedDist;
        return b.maxLat - bbox.minLat > 0;
    }

    // test bottom intersect
    if (lat < b.minLat) {
        if (lon < b.minLon)
            return normDist(b.minLat, b.minLon) <= normedDist;
        if (lon > b.maxLon)
            return normDist(b.minLat, b.maxLon) <= normedDist;
        return bbox.maxLat - b.minLat > 0;
    }

    // test middle intersect
    if (lon < b.minLon)
        return bbox.maxLon - b.minLon > 0;
    if (lon > b.maxLon)
        return b.maxLon - bbox.minLon > 0;
    return true;
  }
}

• minLat, maxLat peuvent être remplacés par minY, Maxx et le même pour minLon, maxLon: le remplacer par minX, maxX
La méthode
• normDist est juste un peu plus rapide que le calcul de la pleine distance. E. g. sans la racine carrée dans l'espace euclidien (ou sans beaucoup d'autres choses pour haversine): dLat=(lat-circleY); dLon=(lon-circleX); normed=dLat*dLat+dLon*dLon . Bien sûr, si vous utilisez cette méthode normDist, vous aurez besoin de créer un normedDist = dist*dist; pour le cercle

voir le code complet BBox et Circle code de mon projet GraphHopper .

pour ceux doivent calculer la collision Cercle/Rectangle dans les coordonnées géographiques avec SQL,

c'est mon implémentation dans oracle 11 de E. James a suggéré l'algorithme .

en entrée, il faut des coordonnées circulaires, un rayon circulaire en km et deux sommets du rectangle:

CREATE OR REPLACE FUNCTION "DETECT_CIRC_RECT_COLLISION"
(
    circleCenterLat     IN NUMBER,      -- circle Center Latitude
    circleCenterLon     IN NUMBER,      -- circle Center Longitude
    circleRadius        IN NUMBER,      -- circle Radius in KM
    rectSWLat           IN NUMBER,      -- rectangle South West Latitude
    rectSWLon           IN NUMBER,      -- rectangle South West Longitude
    rectNELat           IN NUMBER,      -- rectangle North Est Latitude
    rectNELon           IN NUMBER       -- rectangle North Est Longitude
)
RETURN NUMBER
AS
    -- converts km to degrees (use 69 if miles)
    kmToDegreeConst     NUMBER := 111.045;

    -- Remaining rectangle vertices 
    rectNWLat   NUMBER;
    rectNWLon   NUMBER;
    rectSELat   NUMBER;
    rectSELon   NUMBER;

    rectHeight  NUMBER;
    rectWIdth   NUMBER;

    circleDistanceLat   NUMBER;
    circleDistanceLon   NUMBER;
    cornerDistanceSQ    NUMBER;

BEGIN
    -- Initialization of remaining rectangle vertices  
    rectNWLat := rectNELat;
    rectNWLon := rectSWLon;
    rectSELat := rectSWLat;
    rectSELon := rectNELon;

    -- Rectangle sides length calculation
    rectHeight := calc_distance(rectSWLat, rectSWLon, rectNWLat, rectNWLon);
    rectWidth := calc_distance(rectSWLat, rectSWLon, rectSELat, rectSELon);

    circleDistanceLat := abs( (circleCenterLat * kmToDegreeConst) - ((rectSWLat * kmToDegreeConst) + (rectHeight/2)) );
    circleDistanceLon := abs( (circleCenterLon * kmToDegreeConst) - ((rectSWLon * kmToDegreeConst) + (rectWidth/2)) );

    IF circleDistanceLon > ((rectWidth/2) + circleRadius) THEN
        RETURN -1;   --  -1 => NO Collision ; 0 => Collision Detected
    END IF;

    IF circleDistanceLat > ((rectHeight/2) + circleRadius) THEN
        RETURN -1;   --  -1 => NO Collision ; 0 => Collision Detected
    END IF;

    IF circleDistanceLon <= (rectWidth/2) THEN
        RETURN 0;   --  -1 => NO Collision ; 0 => Collision Detected
    END IF;

    IF circleDistanceLat <= (rectHeight/2) THEN
        RETURN 0;   --  -1 => NO Collision ; 0 => Collision Detected
    END IF;


    cornerDistanceSQ := POWER(circleDistanceLon - (rectWidth/2), 2) + POWER(circleDistanceLat - (rectHeight/2), 2);

    IF cornerDistanceSQ <=  POWER(circleRadius, 2) THEN
        RETURN 0;  --  -1 => NO Collision ; 0 => Collision Detected
    ELSE
        RETURN -1;  --  -1 => NO Collision ; 0 => Collision Detected
    END IF;

    RETURN -1;  --  -1 => NO Collision ; 0 => Collision Detected
END;    

fonctionne, Juste compris Il ya une semaine, et juste maintenant à tester.

double theta = Math.atan2(cir.getX()-sqr.getX()*1.0,
                          cir.getY()-sqr.getY()*1.0); //radians of the angle
double dBox; //distance from box to edge of box in direction of the circle

if((theta >  Math.PI/4 && theta <  3*Math.PI / 4) ||
   (theta < -Math.PI/4 && theta > -3*Math.PI / 4)) {
    dBox = sqr.getS() / (2*Math.sin(theta));
} else {
    dBox = sqr.getS() / (2*Math.cos(theta));
}
boolean touching = (Math.abs(dBox) >=
                    Math.sqrt(Math.pow(sqr.getX()-cir.getX(), 2) +
                              Math.pow(sqr.getY()-cir.getY(), 2)));

si vous avez les quatre bords du rectangle, vérifiez la distance entre les bords et le centre du cercle, si elle est inférieure au rayon, alors les formes se croisent.

if sqrt((rectangleRight.x - circleCenter.x)^2 +
        (rectangleBottom.y - circleCenter.y)^2) < radius
// then they intersect

if sqrt((rectangleRight.x - circleCenter.x)^2 +
        (rectangleTop.y - circleCenter.y)^2) < radius
// then they intersect

if sqrt((rectangleLeft.x - circleCenter.x)^2 +
        (rectangleTop.y - circleCenter.y)^2) < radius
// then they intersect

if sqrt((rectangleLeft.x - circleCenter.x)^2 +
        (rectangleBottom.y - circleCenter.y)^2) < radius
// then they intersect

Si le rectangle coupe le cercle, un ou plusieurs points des coins du rectangle doit être à l'intérieur du cercle. Supposons que les quatre points D'un rectangle sont A,B,C,D. au moins l'un d'entre eux devrait croiser le cercle. donc, si la distance d'un point au centre du cercle est inférieur au rayon du cercle dans lequel il doit se coupent le cercle. Pour obtenir la distance, vous pouvez utiliser le théorème de Pythagore,

H^2 = A^2 + B^2

cette technique a des limites. Mais cela fonctionne mieux pour les développeurs de jeux. en particulier la détection des collisions

c'est une bonne mise à jour de L'algorithme D'Arvo