Comment corriger le chevauchement de cercle et de rectangle dans la réponse à une collision?
puisque dans le monde numérique une vraie collision ne se produit presque jamais, nous aurons toujours une situation où le cercle de "collision" chevauche le rectangle.
comment remettre le cercle dans la situation où il entre parfaitement en collision avec le rectangle sans chevauchement?
supposons que le rectangle soit arrêté (vitesse nulle) et aligné sur l'axe.
je voudrais résoudre ce problème avec la a posteriori approche (en deux dimensions).
en résumé, je dois résoudre cette équation pour t :
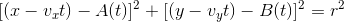
où:
-
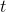 est un nombre qui répond à la question: Combien de cadres il y a fait le
collision arriver à la perfection?
est un nombre qui répond à la question: Combien de cadres il y a fait le
collision arriver à la perfection? -
 est le rayon du cercle.
est le rayon du cercle. -
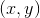 est le centre du cercle
est le centre du cercle -
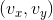 est sa vitesse.
est sa vitesse. -
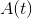 et
et 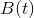 sont des fonctions qui renvoient les coordonnées x et y de
le point où le cercle et le rectangle collision (lorsque le cercle est
sont des fonctions qui renvoient les coordonnées x et y de
le point où le cercle et le rectangle collision (lorsque le cercle est
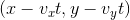 position, qui est dans la position dans laquelle parfaitement entrer en collision avec le rectangle).
position, qui est dans la position dans laquelle parfaitement entrer en collision avec le rectangle).
J'ai récemment résolu un problème similaire pour les collisions entre cercles, mais maintenant je ne connais pas la loi des fonctions A et B.
3 réponses
après des années à regarder ce problème, et sans jamais trouver une solution parfaite, je l'ai finalement fait!
c'est à peu près un algorithme simple, pas besoin de boucle et d'approximations.
C'est comme ça que ça marche à un niveau supérieur:
- calculer les temps d'intersection avec le plan de chaque côté si la trajectoire du point courant au point futur traverse ce plan.
- contrôle le secteur de chaque côté pour l'intersection à un seul côté, retournez l'intersection.
- Déterminez le coin avec lequel le cercle entre en collision.
- résolvez le triangle entre le point courant, le coin et le centre d'intersection (rayon éloigné du coin).
- calculez le temps, la normale et le centre d'intersection.
et maintenant aux détails sanglants!
l'entrée de la fonction est des bornes (qui ont un gauche, haut, droit, bas) et un point courant (début) et un point futur (fin).
La sortie est une classe appelée croisement a x, y, temps, nx et ny.
- {x, y} est le centre du cercle au moment de l'intersection.
- le temps est une valeur de 0 à 1, où 0 est au début et 1 en fin
- {NX, ny} est la normale, utilisée pour reflétant la vitesse pour déterminer la nouvelle vélocité du cercle
nous commençons par les variables de mise en cache que nous utilisons souvent:
float L = bounds.left;
float T = bounds.top;
float R = bounds.right;
float B = bounds.bottom;
float dx = end.x - start.x;
float dy = end.y - start.y;
et calcul des temps d'intersection avec le plan de chaque côté (si le vecteur entre le début et la fin passe par-dessus ce plan):
float ltime = Float.MAX_VALUE;
float rtime = Float.MAX_VALUE;
float ttime = Float.MAX_VALUE;
float btime = Float.MAX_VALUE;
if (start.x - radius < L && end.x + radius > L) {
ltime = ((L - radius) - start.x) / dx;
}
if (start.x + radius > R && end.x - radius < R) {
rtime = (start.x - (R + radius)) / -dx;
}
if (start.y - radius < T && end.y + radius > T) {
ttime = ((T - radius) - start.y) / dy;
}
if (start.y + radius > B && end.y - radius < B) {
btime = (start.y - (B + radius)) / -dy;
}
maintenant nous essayons de voir si c'est strictement une intersection latérale (et non un coin). Si le point de collision se trouve sur le côté puis retourner la intersection:
if (ltime >= 0.0f && ltime <= 1.0f) {
float ly = dy * ltime + start.y;
if (ly >= T && ly <= B) {
return new Intersection( dx * ltime + start.x, ly, ltime, -1, 0 );
}
}
else if (rtime >= 0.0f && rtime <= 1.0f) {
float ry = dy * rtime + start.y;
if (ry >= T && ry <= B) {
return new Intersection( dx * rtime + start.x, ry, rtime, 1, 0 );
}
}
if (ttime >= 0.0f && ttime <= 1.0f) {
float tx = dx * ttime + start.x;
if (tx >= L && tx <= R) {
return new Intersection( tx, dy * ttime + start.y, ttime, 0, -1 );
}
}
else if (btime >= 0.0f && btime <= 1.0f) {
float bx = dx * btime + start.x;
if (bx >= L && bx <= R) {
return new Intersection( bx, dy * btime + start.y, btime, 0, 1 );
}
}
nous sommes arrivés jusqu'ici donc nous savons soit qu'il n'y a pas d'intersection, soit qu'il y a une collision avec un coin. Nous devons déterminer le coin:
float cornerX = Float.MAX_VALUE;
float cornerY = Float.MAX_VALUE;
if (ltime != Float.MAX_VALUE) {
cornerX = L;
} else if (rtime != Float.MAX_VALUE) {
cornerX = R;
}
if (ttime != Float.MAX_VALUE) {
cornerY = T;
} else if (btime != Float.MAX_VALUE) {
cornerY = B;
}
// Account for the times where we don't pass over a side but we do hit it's corner
if (cornerX != Float.MAX_VALUE && cornerY == Float.MAX_VALUE) {
cornerY = (dy > 0.0f ? B : T);
}
if (cornerY != Float.MAX_VALUE && cornerX == Float.MAX_VALUE) {
cornerX = (dx > 0.0f ? R : L);
}
maintenant nous avons assez d'informations pour résoudre le triangle. Cela utilise la formule de distance, trouver l'angle entre deux vecteurs, et la loi de sines (deux fois):
double inverseRadius = 1.0 / radius;
double lineLength = Math.sqrt( dx * dx + dy * dy );
double cornerdx = cornerX - start.x;
double cornerdy = cornerY - start.y;
double cornerdist = Math.sqrt( cornerdx * cornerdx + cornerdy * cornerdy );
double innerAngle = Math.acos( (cornerdx * dx + cornerdy * dy) / (lineLength * cornerdist) );
double innerAngleSin = Math.sin( innerAngle );
double angle1Sin = innerAngleSin * cornerdist * inverseRadius;
// The angle is too large, there cannot be an intersection
if (Math.abs( angle1Sin ) > 1.0f) {
return null;
}
double angle1 = Math.PI - Math.asin( angle1Sin );
double angle2 = Math.PI - innerAngle - angle1;
double intersectionDistance = radius * Math.sin( angle2 ) / innerAngleSin;
maintenant que nous avons résolu pour tous les côtés et les angles, nous pouvons déterminer le temps et tout le reste:
// Solve for time
float time = (float)(intersectionDistance / lineLength);
// If time is outside the boundaries, return null. This algorithm can
// return a negative time which indicates the previous intersection.
if (time > 1.0f || time < 0.0f) {
return null;
}
// Solve the intersection and normal
float ix = time * dx + start.x;
float iy = time * dy + start.y;
float nx = (float)((ix - cornerX) * inverseRadius);
float ny = (float)((iy - cornerY) * inverseRadius);
return new Intersection( ix, iy, time, nx, ny );
Woo! C'était amusant... cela a beaucoup de place pour des améliorations de l'efficacité va. Vous pouvez réordonner la vérification de l'intersection latérale pour vous échapper le plus tôt possible tout en faisant le moins de calculs possible.
j'espérais qu'il y aurait un moyen de le faire sans les fonctions trigonométriques, mais j'ai dû céder!
Voici un exemple de m'appeler et l'utiliser pour calculer le nouveau position du cercle en utilisant la normale pour réfléchir et le temps d'intersection pour calculer l'amplitude de réflexion:
Intersection inter = handleIntersection( bounds, start, end, radius );
if (inter != null)
{
// Project Future Position
float remainingTime = 1.0f - inter.time;
float dx = end.x - start.x;
float dy = end.y - start.y;
float dot = dx * inter.nx + dy * inter.ny;
float ndx = dx - 2 * dot * inter.nx;
float ndy = dy - 2 * dot * inter.ny;
float newx = inter.x + ndx * remainingTime;
float newy = inter.y + ndy * remainingTime;
// new circle position = {newx, newy}
}
et j'ai posté le code complet sur pastebin avec un exemple complètement interactif où vous pouvez tracer les points de départ et de fin et il vous montre le temps et le rebond résultant du rectangle.
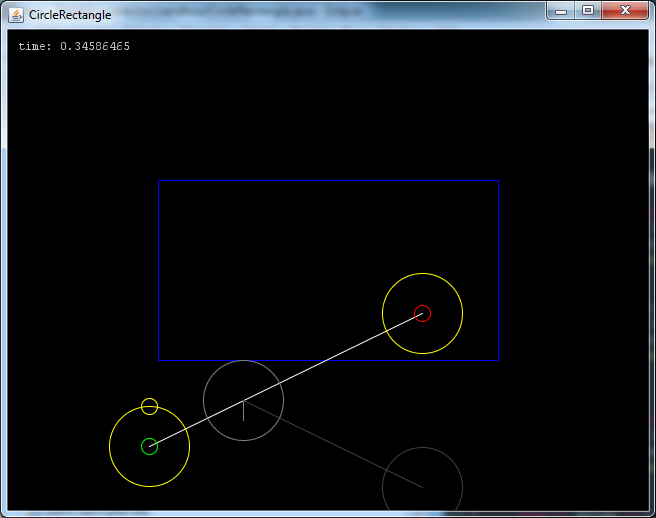
Si vous voulez l'obtenir en cours d'exécution , vous aurez à télécharger le code de mon blog , sinon coller dans votre propre application Java2D.
EDIT: J'ai modifié le code de pastebin pour y inclure le point de collision, et j'ai aussi amélioré la vitesse.
EDIT: Vous pouvez modifier ceci pour un rectangle rotatif en utilisant l'angle de ce rectangle pour dé-tourner le rectangle avec le début de cercle et les points de fin. Vous allez vérifier l'intersection. et puis tourner les points résultants et les normales.
EDIT: J'ai modifié le code sur pastebin pour sortir tôt si le volume limite du chemin du cercle ne se croise pas avec le rectangle.
trouver le moment du contact n'est pas trop difficile:
vous avez besoin de la position du cercle et du rectangle au pas de temps avant la collision (B) et au pas de temps après (a). Calculer la distance du centre du cercle à la ligne du rectangle avec lequel il entre en collision aux temps A et B (c'est à dire, une formule commune pour une distance d'un point à une ligne), et puis le temps de collision est:
tC = dt*(dB-R)/(dA+dB),
où tC est le moment de la collision, dt est le pas de temps, dB est la distance jusqu'à la ligne avant la collision, dA est la distance après la collision, et R est le rayon du cercle.
cela suppose que tout est localement linéaire, c'est-à-dire que vos pas de temps sont raisonnablement petits, et donc que la vitesse, etc, ne change pas beaucoup dans le pas de temps où vous calculez la collision. C'est, après tout, le point d'échéances: avec une assez petite timestep, les problèmes non-linéaires sont localement linéaire. Dans le équation ci-dessus je tire avantage de cela: dB-R est la distance du cercle à la ligne, et dA+dB est la distance totale déplacée, donc cette question égale juste le rapport de distance au rapport de temps en supposant que tout est approximativement linéaire dans le pas de temps. (Bien sûr, au moment de la collision l'approximation linéaire n'est pas son meilleur, mais pour trouver le moment de la collision, la question Est de savoir si elle est linéaire dans un pas de temps jusqu'à au moment de la collision.)
C'est un problème non linéaire, droite?
vous prenez un pas de temps et vous déplacez la boule par son déplacement calculé en utilisant la vitesse au début de l'étape. Si vous trouvez un chevauchement, réduisez la taille de l'étape et recalculez la convergence til.
supposez-vous que les billes et les rectangles sont rigides, sans déformation? Contact sans friction? Comment allez-vous gérer le mouvement de la balle après le contact? Êtes-vous la transformation de coordonnées système du contact (normal + tangentiel), calcul, puis transformation?
ce n'est pas un problème insignifiant.
peut-être que vous devriez regarder dans un moteur de physique, comme Box2D , plutôt que de le coder vous-même.