Calcul du pourcentage de la mesure de la variance pour k-means?

la distorsion, en ce qui concerne Kmeans , est utilisée comme critère d'arrêt (si le changement entre deux itérations est inférieur à un certain seuil, nous supposons la convergence)

si vous voulez le calculer à partir d'un ensemble de points et les centroïdes, vous pouvez faire ce qui suit (le code est dans MATLAB en utilisant pdist2 fonction, mais il devrait être simple à réécrire en Python/Numpy/Scipy):

% data
X = [0 1 ; 0 -1 ; 1 0 ; -1 0 ; 9 9 ; 9 10 ; 9 8 ; 10 9 ; 10 8];

% centroids
C = [9 8 ; 0 0];

% euclidean distance from each point to each cluster centroid
D = pdist2(X, C, 'euclidean');

% find closest centroid to each point, and the corresponding distance
[distortions,idx] = min(D,[],2);

le résultat:

% total distortion
>> sum(distortions)
ans =
           9.4142135623731

EDIT#1:

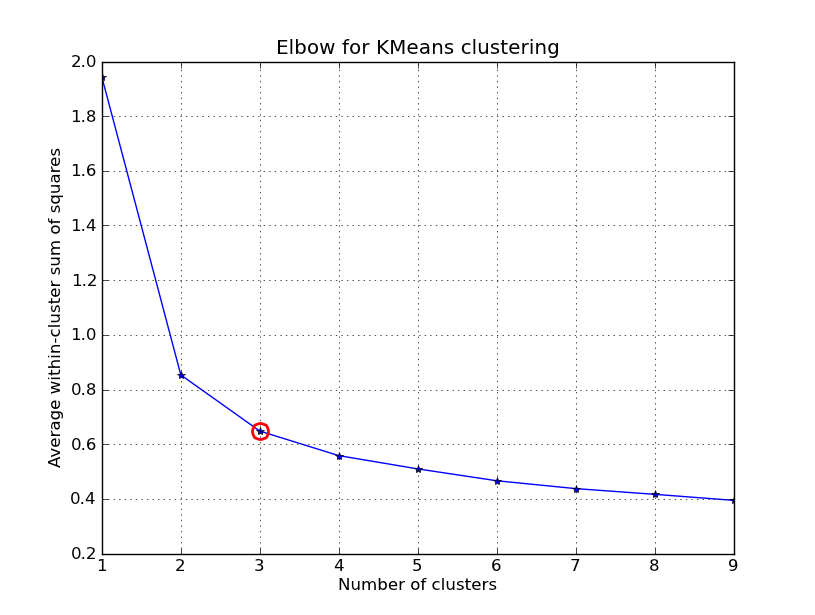
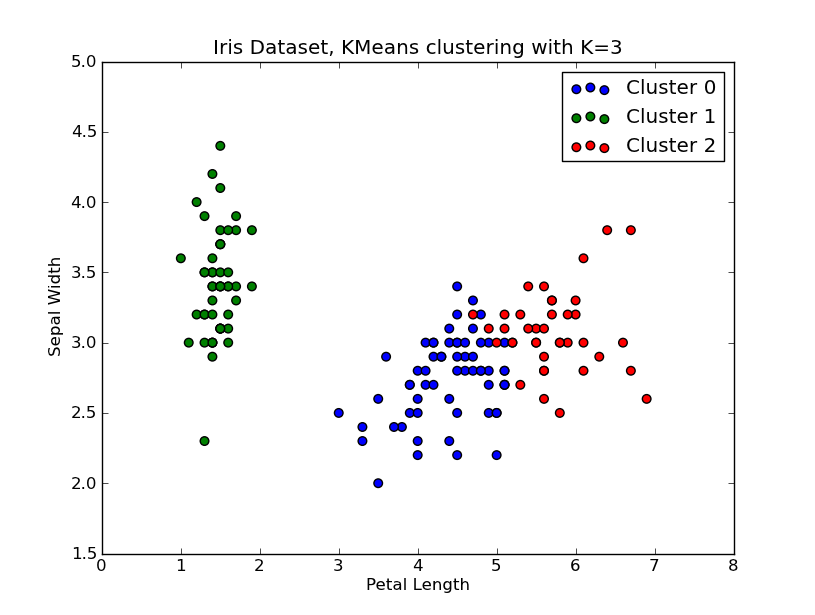
j'ai eu le temps de jouer avec ça.. Voici un exemple de clustering KMeans appliqué sur le 'Fisher Iris Dataset' (4 Caractéristiques, 150 instances). Nous itérons sur k=1..10 , traçons la courbe du coude, choisissons K=3 comme nombre de grappes, et montrons un nuage de points du résultat.

noter que J'ai inclus un certain nombre de façons de calculer les variances à l'intérieur d'un groupe (distorsions), compte tenu des points et des centroïdes. La fonction scipy.cluster.vq.kmeans renvoie cette mesure par défaut (calculée avec Euclide comme mesure de distance). Vous pouvez également utiliser la fonction scipy.spatial.distance.cdist pour calculer les distances avec la fonction de votre choix (à condition que vous ayez obtenu les centroïdes de groupe en utilisant la même mesure de distance: @Denis avez une solution pour ça), puis calculer la distorsion.

import numpy as np
from scipy.cluster.vq import kmeans,vq
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt

# load the iris dataset
fName = 'C:\Python27\Lib\site-packages\scipy\spatial\tests\data\iris.txt'
fp = open(fName)
X = np.loadtxt(fp)
fp.close()

##### cluster data into K=1..10 clusters #####
K = range(1,10)

# scipy.cluster.vq.kmeans
KM = [kmeans(X,k) for k in K]
centroids = [cent for (cent,var) in KM]   # cluster centroids
#avgWithinSS = [var for (cent,var) in KM] # mean within-cluster sum of squares

# alternative: scipy.cluster.vq.vq
#Z = [vq(X,cent) for cent in centroids]
#avgWithinSS = [sum(dist)/X.shape[0] for (cIdx,dist) in Z]

# alternative: scipy.spatial.distance.cdist
D_k = [cdist(X, cent, 'euclidean') for cent in centroids]
cIdx = [np.argmin(D,axis=1) for D in D_k]
dist = [np.min(D,axis=1) for D in D_k]
avgWithinSS = [sum(d)/X.shape[0] for d in dist]

##### plot ###
kIdx = 2

# elbow curve
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(K, avgWithinSS, 'b*-')
ax.plot(K[kIdx], avgWithinSS[kIdx], marker='o', markersize=12, 
    markeredgewidth=2, markeredgecolor='r', markerfacecolor='None')
plt.grid(True)
plt.xlabel('Number of clusters')
plt.ylabel('Average within-cluster sum of squares')
plt.title('Elbow for KMeans clustering')

# scatter plot
fig = plt.figure()
ax = fig.add_subplot(111)
#ax.scatter(X[:,2],X[:,1], s=30, c=cIdx[k])
clr = ['b','g','r','c','m','y','k']
for i in range(K[kIdx]):
    ind = (cIdx[kIdx]==i)
    ax.scatter(X[ind,2],X[ind,1], s=30, c=clr[i], label='Cluster %d'%i)
plt.xlabel('Petal Length')
plt.ylabel('Sepal Width')
plt.title('Iris Dataset, KMeans clustering with K=%d' % K[kIdx])
plt.legend()

plt.show()

EDIT#2:

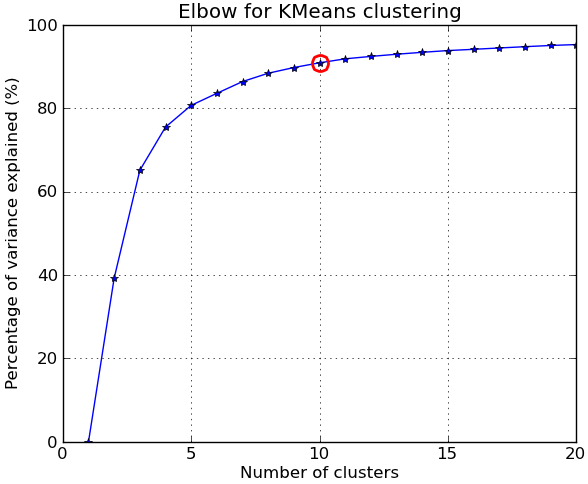
en réponse aux commentaires, je donne ci-dessous un autre exemple complet en utilisant le NIST main-written digits dataset : il a 1797 images de chiffres de 0 à 9, chacun de taille 8 par 8 pixels. Je répéter l'expérience ci-dessus légèrement modifié: L'analyse des composants principaux est appliquée pour réduire la dimensionnalité de 64 à 2:

import numpy as np
from scipy.cluster.vq import kmeans
from scipy.spatial.distance import cdist,pdist
from sklearn import datasets
from sklearn.decomposition import RandomizedPCA
from matplotlib import pyplot as plt
from matplotlib import cm

##### data #####
# load digits dataset
data = datasets.load_digits()
t = data['target']

# perform PCA dimensionality reduction
pca = RandomizedPCA(n_components=2).fit(data['data'])
X = pca.transform(data['data'])

##### cluster data into K=1..20 clusters #####
K_MAX = 20
KK = range(1,K_MAX+1)

KM = [kmeans(X,k) for k in KK]
centroids = [cent for (cent,var) in KM]
D_k = [cdist(X, cent, 'euclidean') for cent in centroids]
cIdx = [np.argmin(D,axis=1) for D in D_k]
dist = [np.min(D,axis=1) for D in D_k]

tot_withinss = [sum(d**2) for d in dist]  # Total within-cluster sum of squares
totss = sum(pdist(X)**2)/X.shape[0]       # The total sum of squares
betweenss = totss - tot_withinss          # The between-cluster sum of squares

##### plots #####
kIdx = 9        # K=10
clr = cm.spectral( np.linspace(0,1,10) ).tolist()
mrk = 'os^p<dvh8>+x.'

# elbow curve
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(KK, betweenss/totss*100, 'b*-')
ax.plot(KK[kIdx], betweenss[kIdx]/totss*100, marker='o', markersize=12, 
    markeredgewidth=2, markeredgecolor='r', markerfacecolor='None')
ax.set_ylim((0,100))
plt.grid(True)
plt.xlabel('Number of clusters')
plt.ylabel('Percentage of variance explained (%)')
plt.title('Elbow for KMeans clustering')

# show centroids for K=10 clusters
plt.figure()
for i in range(kIdx+1):
    img = pca.inverse_transform(centroids[kIdx][i]).reshape(8,8)
    ax = plt.subplot(3,4,i+1)
    ax.set_xticks([])
    ax.set_yticks([])
    plt.imshow(img, cmap=cm.gray)
    plt.title( 'Cluster %d' % i )

# compare K=10 clustering vs. actual digits (PCA projections)
fig = plt.figure()
ax = fig.add_subplot(121)
for i in range(10):
    ind = (t==i)
    ax.scatter(X[ind,0],X[ind,1], s=35, c=clr[i], marker=mrk[i], label='%d'%i)
plt.legend()
plt.title('Actual Digits')
ax = fig.add_subplot(122)
for i in range(kIdx+1):
    ind = (cIdx[kIdx]==i)
    ax.scatter(X[ind,0],X[ind,1], s=35, c=clr[i], marker=mrk[i], label='C%d'%i)
plt.legend()
plt.title('K=%d clusters'%KK[kIdx])

plt.show()

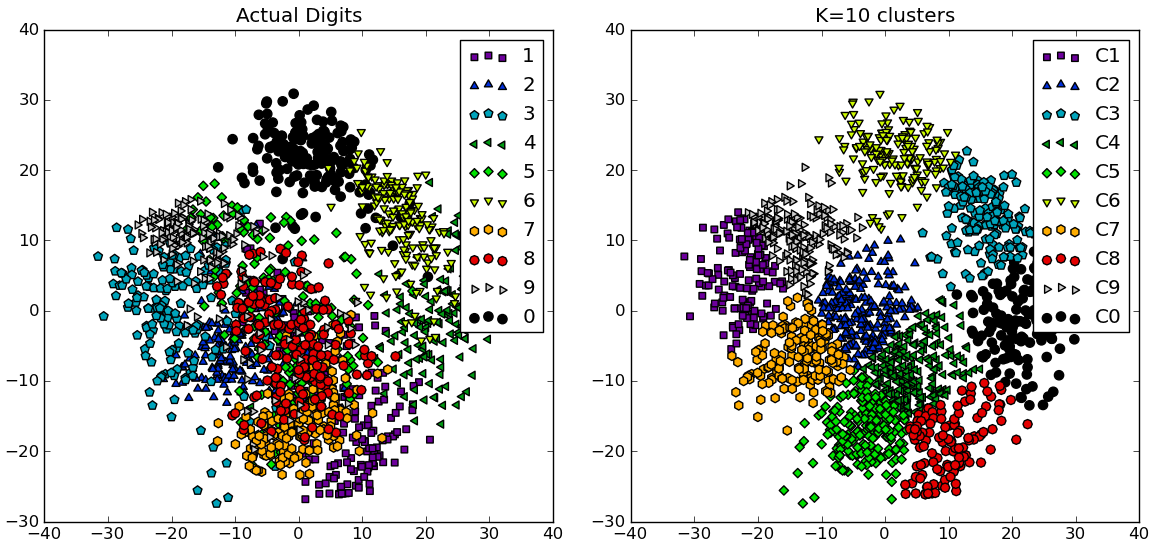
vous pouvez voir comment certains groupes correspondent en fait à des chiffres identifiables, tandis que d'autres ne correspondent pas à un seul nombre.

Note: la mise en œuvre de k-means est inclus dans scikit-learn (ainsi que de nombreux autres algorithmes de clustering et de divers clustering mesures ). ici est un autre exemple similaire.

Un simple cluster mesure:

1) tirer des rayons "sunburst" de chaque point à son centre d'amas le plus proche,

2) regardez les longueurs-distance (point, centre, métrique=... ) - de tous les rayons.

pour metric="sqeuclidean" et 1 cluster, la longueur moyenne au carré est la variance totale X.var() ; pour 2 grappes, c'est moins ... jusqu'à n grappes, longueurs toutes 0. "Pourcentage de la variance expliquée" est de 100 % - cette moyenne.

Code pour cela, dans la section est-il-possible-de-indiquez-votre-propre-distance-fonction-aide-scikits-apprendre-k-means :

def distancestocentres( X, centres, metric="euclidean", p=2 ):
    """ all distances X -> nearest centre, any metric
            euclidean2 (~ withinss) is more sensitive to outliers,
            cityblock (manhattan, L1) less sensitive
    """
    D = cdist( X, centres, metric=metric, p=p )  # |X| x |centres|
    return D.min(axis=1)  # all the distances

comme n'importe quelle longue liste de nombres, ces distances peuvent être regardées de différentes manières: np.moyenne(), np.histogramme. )(.. Le traçage, la visualisation n'est pas facile.

Voir aussi stats.stackexchange.com/questions/tagged/clustering , en particulier

Comment dire si les données sont suffisamment "regroupées" pour que les algorithmes de regroupement produisent des résultats significatifs?