XOR opération Intuition

L'opérateur Xor est commutatif :

1.      X ⊕ Y = Y ⊕ X                    for any integers X and Y

Et associatif:

2.      X ⊕ (Y ⊕ Z) = (X ⊕ Y) ⊕ Z      for any integers X, Y and Z

Il s'ensuit que le résultat de toute séquence d'opérations xor est complètement indépendant de l'ordre des opérandes (c'est-à-dire de l'ordre des éléments du tableau).

3.     X ⊕ X = 0                         for any integer X

4.     X ⊕ 0 = 0 ⊕ X = X                for any integer X

Dans le problème, nous avons une expression où chaque élément Ai apparaît deux fois sauf un élément singulier B. l'opération XOR résultante est équivalente à:

     (A1 ⊕ A1) ⊕ (A2 ⊕ A2) ⊕    ...   ⊕ B
 = 
         0      ⊕      0     ⊕    ...   ⊕ B
 = 
         B

Quoi sortes de mots-clés dois-je faire attention pour comprendre que je devrais utiliser une opération XOR pour cette question

Certains problèmes peuvent être résolus rapidement en utilisant la manipulation des bits. Après vous être familiarisé avec les opérateurs booléens et leurs propriétés, et avoir vu suffisamment d'applications comme celle-ci, vous vous sentirez naturellement quand elles sont utiles pour résoudre un problème donné.

L'aspect intuitif clé qui distingue XOR des autres opérateurs logiques est qu'il est sans perte, ou non-lossy , ce qui signifie que, contrairement à et , et ou (et plus similaire à Pas à cet égard), il est déterministe réversible: vous pouvez récupérer exactement l'une des valeurs d'entrée étant donné le reste de l'historique de calcul.

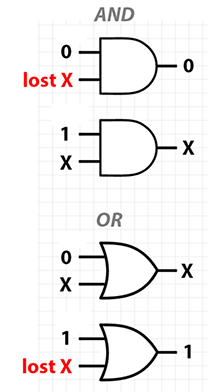
Les schémas suivants illustrent le fait que ET et OU ont chacun au au moins un cas où l'état de l'une des entrées est irrécupérable, compte tenu d'une certaine valeur de l'autre entrée. Je les indique comme des entrées "Perdues".

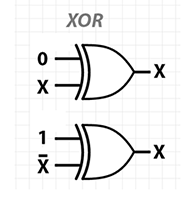
Pour la porte XOR , Il n'y a pas de condition dans laquelle une valeur d'entrée ou de sortie ne peut pas être récupérée, étant donné le reste de l'historique de calcul. En fait, il y a une symétrie que connaître deux valeurs quelconques du triple (in0, in1, out) vous permet de récupérer la troisième. En d'autres termes, quelle que soit l'entrée ou en sortie, chacune de ces trois valeurs est la XOR des deux autres!

Cette image suggère qu'une autre façon de penser à l'opération XOR est comme une porte contrôlable et non. En basculant l'une des entrées (la supérieure dans l'exemple ci-dessus), vous pouvez contrôler si l'autre (inférieure) est annulée ou non.

Une autre vue équivalente est que XOR implémente la logique positive non-égal à (∞) fonction par rapport à ses deux entrées. Et donc aussi laégale FONCTION ( = ) sous logique négative .

Conformément à ses propriétés de symétrie et de préservation de l'information, XOR devrait venir à l'esprit pour les problèmes qui nécessitent une réversibilité ou une récupération de données parfaite. L'exemple le plus évident est que XOR ing un ensemble de données avec une 'clé' constante obscurcit trivialement les données de sorte que connaître la clé (qui pourrait être gardée "secrète"), permet d'obtenir des données exactes récupération.

La préservation de toutes les informations disponibles est également souhaitable dans hashing . Parce que vous voulez des valeurs de hachage qui discriminent au maximum parmi les éléments source, vous voulez vous assurer que le plus grand nombre de leurs caractéristiques distinctives possibles sont incorporées, minimisant la perte, dans le code de hachage. Par exemple, pour hacher une valeur 64 bits en 32 bits, vous utiliserez le langage de programmation XOR operator ^ car c'est un moyen facile de garantir que chaque des 64 bits d'entrée a la possibilité d'influencer la sortie:

uint GetHashCode(ulong ul)
{
    return (uint)ul ^ (uint)(ul >> 32); 
}

Notez que dans cet exemple, les informations sont perdues même si XOR a été utilisé. (En fait ‘la "perte d'informations stratégiques" est en quelque sorte le but du hachage). La valeur d'origine de ul n'est pas récupérable à partir du code de hachage, car avec cette valeur seule, vous n'avez pas deux des trois valeurs de 32 bits utilisées dans le calcul interne. Rappelez-vous d'en haut que vous devez conserver deux des trois valeurs pour une inversion parfaite. À partir du code de hachage résultant et des deux valeurs qui étaient XORed, vous avez peut-être enregistré le résultat, mais généralement ne sauvegardez aucune de ces dernières pour l'utiliser comme valeur clé pour obtenir l'autre.¹

Comme un côté amusant, XOR était particulièrement utile à l'époque de bit-twiddling hacks. Ma contribution à l'époque était un moyen de conditionnellement définir ou effacer des bits sans brancher en C / C++:

unsigned int v;       // the value to modify
unsigned int m;       // mask: the bits to set or clear
int f;                // condition: 0 to 'set', or 1 to 'clear'

v ^= (-f ^ v) & m;    // if (f) v |= m; else v &= ~m;

Sur un note plus sérieuse, le fait que XOR est non-lossy a des implications informations-théoriques importantes pour l'informatique futuriste, en raison d'une relation importante entre le traitement de l'information et la deuxième loi de la thermodynamique. Comme expliqué dans un livre excellent et accessible par Charles Seife, décoder L'univers, Il s'avère que la perte d'informations pendant le calcul a une relation mathématique exacte avec le rayonnement corps noir émis par un système de traitement. En effet, la notion de entropie joue un rôle central dans la quantification de la façon dont la "perte" d'information est (re-)exprimée en chaleur (ceci étant également la même relation importante du célèbre pari black hole de Steven Hawking).

Un tel discours concernant XOR n'est pas nécessairement un étirement; Seife note que le développement du processeur moderne fait actuellement face à des limitations fondamentales de tolérance sur le watts / cm2 {[9] } de matériaux semi-conducteurs, et qu'une solution serait de concevoir des systèmes informatiques réversibles, ou sans perte. Dans cette future génération spéculative de processeurs, la capacité de XOR à préserver l'information - et donc à éloigner la chaleur - serait inestimable pour augmenter la densité de calcul (c'est-à-dire MIPS/par cm2) malgré ces limitations matérielles.

XOR est toujours défini en termes de chiffres binaires (ou de notions équivalentes, comme TRUE ou false statements). Il n'y a pas de XOR spécial pour les entiers autres que le XORing des bits correspondants de leurs représentations binaires.

Que A et B soient deux variables booléennes, et que XOR soit une fonction booléenne qui prend deux variables booléennes.
A⊕B = 1 si A = 0 et B = 1) ou (A = 1 et B = 0) (c'est à dire qu'ils sont différents),
A⊕B=0 si A = 0 et B = 0) ou (A = 1 et B = 1). (c'est-à-dire qu'ils sont identiques)

Prenant ainsi en considération votre question puisque sur n éléments donnés du vecteur, chaque élément apparaît deux fois sauf un élément, l'idée est que la représentation binaire des nombres en double serait la même, donc il y aurait un résultat XOR qui s'annulerait comme 1 1 1 = 0 et 0 0 0 = 0.

Pour a = 5, sa représentation binaire est 101, donc A A A = (101)⊕(101) = 000 Quelle est la représentation décimale est 0.

RAPPELEZ-VOUS QU'IL N'A PAS D'IMPORTANCE DANS QUEL ORDRE LES NOMBRES APPARAISSENT APRÈS L'AUTRE PARCE QUE ((A B B)C C) = (A⊕(B C C)). Finalement, ce que vous obtenez à la fin après XORING chaque nombre est le nombre qui se produit Une fois .

Pour répondre à votre question concernant le moment où vous devez utiliser des opérations XOR pour résoudre une question, pratiquez une question de MANIPULATION de bits que vous pourrez éventuellement résoudre.
Un indice: la question qui demande de trouver un élément qui a une propriété unique en dehors de rest, nécessite peu manipulation.
Exemple: étant donné un tableau où chaque élément se produit trois fois, sauf un élément qui ne se produit qu'une seule fois. Trouvez l'élément qui se produit Une fois .

Une opération simple qui peut être fait sur le tableau est de choisir une propriété P et compter le nombre d'éléments du tableau qui satisfont la propriété. Par exemple, si P est la propriété d'être divisible par 5, nous pouvons parcourir le tableau et de compter le nombre d'éléments qui sont divisibles par 5.

La condition préalable sur le tableau nous permet d'obtenir des informations sur l'élément singleton à partir d'un tel nombre. Si le nombre d'éléments satisfaisant P est impair, alors le singleton a la propriété P. Si le nombre d'éléments satisfaisant P est pair, alors le singleton ne doit pas avoir la propriété P. Par exemple, si nous comptons 3 éléments divisibles par 5, alors le singleton doit avoir été divisible par 5.

Par conséquent, si nous pouvons inventer une collection de propriétés de telle sorte que savoir si chaque propriété est vraie ou fausse spécifiera complètement n'importe quel élément, nous pouvons obtenir la réponse en comptant le nombre d'éléments avec chaque propriété et en vérifiant la parité du compter.

Il y a beaucoup de différentes collections de propriétés qui fonctionneront. Nous pouvons aussi bien être efficaces, cependant. Étant donné b différentes propriétés, il y a (au plus) 2**b différentes façons dont les tests pourraient sortir, donc nous ne pouvons que distinguer parmi ces nombreux éléments possibles. Donc, nous avons besoin d'au moins b différentes propriétés pour spécifier entièrement b-nombre de bits.

Une telle collection minimale de propriétés facile à tester par un ordinateur est la collection où nth propriété est "le nombre de 1 dans le nth bits?". Si nous connaissons la réponse à cette question pour chaque n, alors clairement nous pouvons reconstruire le nombre.

Une autre optimisation est que nous n'avons pas besoin de garder une trace du nombre total d'éléments satisfaisant une propriété; nous avons seulement besoin de la parité. Si nous gardons juste une trace du nombre modulo 2, alors nous n'avons besoin que d'un bit pour garder une trace au lieu d'un entier size_t.

Puisque nous gardons une trace de b différents bits de informations, chacune correspondant à une valeur de lieu particulière n, nous pouvons assembler ces bits ensemble dans un nombre b-bit.

C'est exactement la solution XOR présentée dans la question.

Pour commencer, le nombre de nombres ayant chaque bit est 0 pour chaque bit (par conséquent result est initialisé à 0). Ensuite, lorsque nous XOR un élément du tableau, nous ajoutons en fait un modulo 2 à ces bits de result où l'élément avait un 1. Enfin, result fait ne nécessite aucun décodage, car le nombre avec 1 bits exactement où result a 1 bits est result lui-même.

Comme je suis sûr que vous êtes familier avec, les entiers sont stockés en mémoire sous forme de tuples de chiffres binaires. On peut voir chaque chiffre comme un nombre dans le champ de deux éléments, qui est essentiellement des entiers modulo 2. L'opérateur ^ est XOR par composant, et avec cette interprétation, xor est simplement addition . Autrement dit, nous ajoutons les chiffres binaires les uns avec les autres.

Dans ce champ, 1 + 1 = 0, donc on peut dire que deux est zéro. Puisque l'addition est commutative et associative nous pouvons combiner tous les chiffres à la fois. Tout ce qui est ajouté un nombre pair de fois n'ajoutera rien, et seul le nombre ajouté une seule fois finit dans la variable de résultat.

Il pourrait être intéressant de savoir que les opérations booléennes sont représentées de cette façon comme (essayez-le!): a xor b = a + b, a et b = ab, ou b = ab + a + b, pas a = a + 1.