Pourquoi un tas de Fibonacci s'appelle un tas de Fibonacci?
le Fibonacci tas structure de données a le mot "Fibonacci" dans son nom, mais rien dans la structure de données semble utiliser des nombres Fibonacci. Selon L'article de Wikipedia:
le nom de Fibonacci tas vient des nombres de Fibonacci qui sont utilisés dans l'analyse du temps de course.
comment ces nombres de Fibonacci apparaissent-ils dans le tas de Fibonacci?
2 réponses
le tas de Fibonacci est constitué d'une collection de petits arbres ordonnés en tas de différents "ordres" qui obéissent à certaines contraintes structurelles. La séquence de Fibonacci se produit parce que ces arbres sont construits d'une manière telle qu'un arbre de l'ordre n a au moins F n+2 Noeuds en elle, où F n+2 est le (n + 2)nd nombre de Fibonacci.
pour voir pourquoi ce résultat est vrai, commençons par voir comment les arbres dans le Fibonacci tas sont construits. Au départ, chaque fois qu'un noeud est placé dans un tas de Fibonacci, il est placé dans un arbre d'ordre 0 qui contient juste ce noeud. Chaque fois qu'une valeur est retirée du tas de Fibonacci, certains arbres du tas de Fibonacci sont fusionnés de sorte que le nombre d'arbres ne grossit pas trop.
lorsqu'on combine des arbres ensemble, le tas de Fibonacci ne combine que des arbres du même ordre. Pour combiner deux arbres de l'ordre n Dans un arbre de ordre n + 1, le tas de Fibonacci prend celui des deux arbres qui a une plus grande valeur racine que l'autre, puis fait de cet arbre un enfant de l'Autre Arbre. Une conséquence de ce fait est que arbres de l'ordre n ont toujours exactement n enfants .
l'attraction principale du tas de Fibonacci est qu'il supporte la diminution-clé efficacement (dans amorti O(1)). Pour soutenir cela, le tas de Fibonacci met en œuvre la diminution-clé comme suit: diminuer la clé d'une valeur stockée dans certains nœud, ce nœud est coupé de son arbre-mère et traité comme son propre arbre. Lorsque cela se produit, l'ordre de son ancien noeud parent est diminué d'un. Par exemple, si une commande de 4 arbre a un enfant coupé de lui, il se rétrécit à une commande 3 de l'arbre, ce qui est logique, car l'ordre d'un arbre est censé être le nombre d'enfants qu'il contient.
Le problème avec cela est que si trop d'arbres sont coupés de la même arbre, nous pourrions avoir un arbre avec un grand ordre, mais qui contient un très petit nombre de nœuds. Les garanties de temps D'un tas de Fibonacci ne sont possibles que si les arbres avec de grandes commandes contiennent un grand nombre de noeuds, et si nous pouvons juste couper n'importe quels noeuds que nous aimerions des arbres nous pourrions facilement entrer dans une situation où un arbre avec une commande énorme ne contient qu'un petit nombre de noeuds.
pour répondre à cela, les tas de Fibonacci font une exigence - si vous coupez deux enfants d'un arbre, vous devez à votre tour couper cet arbre de son parent. cela signifie que les arbres qui forment un tas de Fibonacci ne seront pas trop endommagés par la décroissance.
et maintenant nous pouvons obtenir la partie sur les nombres de Fibonacci. À ce stade, nous pouvons dire ce qui suit au sujet des arbres dans un tas de Fibonacci:
- Un arbre d'ordre n a exactement n enfants.
- les arbres de l'ordre n sont formés en prenant deux arbres d'ordre n - 1 et de faire de l'enfant de l'autre.
- si un arbre perd deux enfants, il est coupé de ses parents.
alors maintenant nous pouvons nous demander - quels sont les plus petits arbres possibles que vous pouvez faire selon ces hypothèses?
essayons quelques exemples. Il n'y a qu'un seul arbre possible d'ordre 0, qui est un seul noeud:
Smallest possible order 0 tree: *
le plus petit arbre possible de ordre 1 aurait du être au moins un noeud avec un enfant. Le plus petit enfant possible que nous pourrions faire est un noeud simple avec le plus petit arbre d'ordre 0 comme un enfant, qui est cet arbre:
Smallest possible order 1 tree: *
|
*
Qu'en est-il du plus petit arbre de l'ordre 2? C'est là que les choses deviennent intéressantes. Cet arbre doit certainement avoir deux enfants, et il serait formé en fusionnant deux arbres de l'ordre 1. Par conséquent, l'arbre aurait initialement deux enfants - un arbre d'ordre 0 et un arbre de commande 1. Mais rappelez - vous-nous pouvons couper les enfants des arbres après les avoir fusionnés! Dans ce cas, si nous couper l'enfant de l'arbre d'ordre 1, il ne nous reste que un arbre avec deux enfants, qui sont tous deux arbres d'ordre 0:
Smallest possible order 2 tree: *
/ \
* *
et l'ordre 3? Comme auparavant, cet arbre serait fait en fusionnant deux arbres de l'ordre 2. Nous essaierions alors de couper autant de sous-arbres de cet ordre-3 que possible. Au moment de sa création, l'arbre a sous-ordres 2, 1 et 0. Nous ne pouvons pas couper l'arbre de l'ordre 0, mais nous pouvons couper un seul enfant de l'ordre 2 et l'arbre de l'ordre 1. Si nous faisons cela, nous nous retrouvons avec un arbre avec trois enfants, l'un d'ordre 1, et deux d'ordre 2:
Smallest possible order 3 tree: *
/|\
* * *
|
*
maintenant nous pouvons repérer un modèle. Le plus petit arbre d'ordre-(n + 2) possible serait formé comme suit: commencez par créer un arbre d'ordre normal (n + 2), qui a des enfants d'ordres n + 1, n, n - 1, ... 2, 1, 0. Ensuite, faire ces arbres aussi petits que possible en coupant des noeuds d'eux sans couper deux enfants du même noeud. Cela laisse un arbre avec des enfants de commandes n, n - 2, ..., 1, 0 et 0.
nous pouvons maintenant écrire une relation de récurrence pour essayer de déterminer combien de noeuds sont dans ces arbres. Si nous faisons cela, nous obtenons ce qui suit, où NC (n) représente le plus petit nombre de noeuds qui pourraient être dans un arbre d'ordre n:
NC(0) = 1
NC(1) = 2
NC(n + 2) = NC(n) + NC(n - 1) + ... + NC(1) + NC(0) + NC(0) + 1
ici, la finale +1 comptes pour le nœud racine.
si nous élargissons ces termes, nous obtenons ce qui suit:
NC(0) = 1
NC(1) = 2
NC(2) = NC(0) + NC(0) + 1 = 3
NC(3) = NC(1) + NC(0) + NC(0) + 1 = 5
NC(4) = NC(2) + NC(1) + NC(0) + NC(0) + 1 = 8
si vous remarquez, c'est exactement la série Fibonacci décalée de deux positions. En d'autres termes, chacun de ces arbres doit avoir au moins F n+2 nœuds, où F n + 2 est le (n + 2)ème nombre de Fibonacci.
alors pourquoi ça s'appelle un tas de Fibonacci? Parce que chaque arbre de l'ordonnance n doit avoir au moins F n+2 nœuds!
si vous êtes curieux, le papier original sur Fibonacci tas a des photos de ces plus petits arbres possibles. C'est assez chouette à voir!
Espérons que cette aide!
je veux donner une explication intuitive que j'ai moi-même eu un "Aha!"moment avec.
l'Arbre des structures de parvenir à O(log n) temps de fonctionnement, parce qu'ils sont capables de stocker exponentielle du nombre d'articles en fonction de leurs hauteurs. Les arbres binaires peuvent stocker 2^h, les arbres tri-naires 3^h et ainsi de suite pour x^H comme cas Générique.
est-ce que x peut être inférieur à 2? Sûr qu'il peut! Aussi longtemps que x > 1, nous atteignons des temps d'exécution logarithmiques et la capacité de stocker exponentiellement grand nombre de pièces pour sa hauteur. Mais comment pouvons-nous construire un tel arbre? Fibonacci heap est une structure de données où x ≈ 1,62, ou Golden Ratio . Chaque fois que nous rencontrons le Ratio D'Or, il y a des nombres de Fibonacci qui rôdent quelque part...
Fibonacci heap est en fait une forêt d'arbres. Après un processus appelé "consolidation", chacun de ces arbres détient un nombre distinct d'articles qui sont des puissances exactes de 2. Par exemple, si votre tas de Fibonacci a 15 articles, il serait 4 arbres 1, 2, 4 et 8 points respectivement comme ceci:
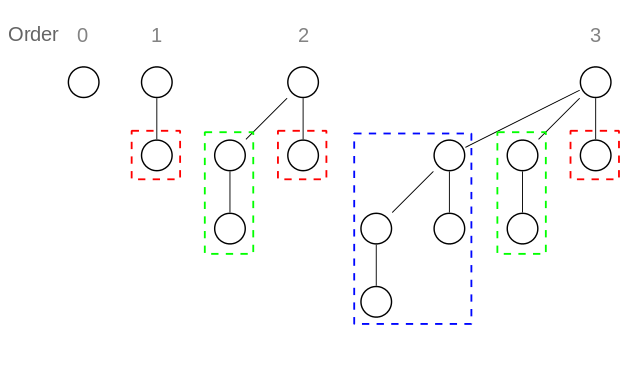
les détails du processus de " consolidation "ne sont pas pertinents, mais essentiellement il maintient les arbres unioning dans la forêt du même degré jusqu'à ce que tous les arbres ont un degré distinct (essayez un visualisation cool pour voir comment ces arbres sont construits). Comme vous pouvez l'écrire n comme somme des puissances de 2, il est facile d'imaginer comment les arbres consolidés pour Fibonacci heap ressembleraient à n'importe quel N.
OK, jusqu'à présent nous ne voyons toujours pas de connexion directe avec les nombres de Fibonacci. D'où viennent-ils dans l'image? Ils apparaissent en fait dans le cas très spécial et c'est également une clé pour pourquoi Fibonacci heap peut offrir O(1) temps pour L'opération de diminution-clé. Quand nous diminuons une clé, si la nouvelle clé est encore plus grande que la clé de parent alors nous n'avons pas besoin de faire autre chose parce que la propriété min-heap n'est pas violée. Mais si elle n'est pas alors on ne peut pas laisser un enfant plus petit enterré sous un parent plus grand et donc on doit le couper en sous-bois et en faire un nouvel arbre. Évidemment, nous ne pouvons pas continuer à faire cela pour chaque suppression car sinon nous finirons avec des arbres qui sont trop hauts et n'ont plus d'éléments exponentiels ce qui signifie plus de temps O(log n) Pour l'opération d'extraction. La question est donc de savoir quelle règle peut-on mettre en place pour que l'arbre ait encore des items exponentiels pour sa hauteur? La perspicacité intelligente est celle-ci:
We will allow each parent to loose up to one child. If there is a subsequent attempt to remove another child from same parent then we will cut that parent also out of that tree and put it in root list as tree of 1.
au-dessus de la règle s'assure que les arbres ont encore des éléments exponentiels pour sa hauteur, même dans le pire des cas. Ce qui est le pire des cas? Le pire se produit lorsque nous faisons perdre un enfant à chaque parent. Si le parent a > 1 enfant, nous avons le choix, qui l'en débarrasser. Dans ce cas, débarrassons-nous de l'enfant avec le plus grand sous-arbre. Donc, dans le schéma ci-dessus, si vous faites cela pour chaque parent, vous devez arbres de la taille 1, 1, 2 et 3. Voir un modèle ici? Juste pour le plaisir, Ajouter un nouvel arbre de ordre 4 (c.-à-d. 16 éléments) dans le diagramme ci-dessus et devinez ce qui vous resterait après avoir exécuté cette règle pour chaque parent: 5. Nous avons une séquence de Fibonacci ici!
comme la séquence de Fibonacci est exponentielle, chaque arbre conserve encore un nombre exponentiel d'articles et parvient ainsi à avoir une durée D'exécution O(log n) pour le fonctionnement EXTRACT-MIN. Notez cependant que DECREASE-KEY ne prend plus que O (1). Une autre chose cool est que vous pouvez représenter n'importe quel nombre comme une somme de nombres de Fibonacci. Pour exemple, 32 = 21 + 8 + 3 ce qui signifie que si vous aviez besoin de tenir 32 articles dans le tas de Fibonacci, vous pouvez le faire en utilisant 3 arbres tenant 21, 8 et 3 articles respectivement. Cependant le processus de "consolidation" ne produit pas les arbres avec le nombre de Fibonacci des noeuds. Ils ne se produisent que lorsque ce cas pire de diminution-clé ou supprimer se produit.
"autre lecture
- Binomial tas - les tas de Fibonacci sont essentiellement des tas binomiaux paresseux. C'est une structure de données cool parce qu'elle montre une façon différente de stocker des éléments exponentiels dans un arbre pour sa hauteur autre que binaire tas.
- l'Intuition derrière les Tas de Fibonacci une lecture Obligatoire pour quiconque veut comprendre les tas de Fibonacci à sa base. Les manuels sont souvent trop superficiels et trop encombrés sur ce sujet, mais l'auteur de cette réponse a cloué les mains.