Pourquoi ne numpy (mts) donner un résultat différent de matlab (mts)?
J'essaie de convertir le code matlab en numpy et j'ai compris que numpy a un résultat différent avec la fonction std.
Dans matlab
std([1,3,4,6])
ans = 2.0817
Dans numpy
np.std([1,3,4,6])
1.8027756377319946
Est-ce normal? Et comment dois-je gérer cela?
3 réponses
La fonction NumPy np.std prend un paramètre optionnel ddof: "Delta Degrés de Liberté". Par défaut, c'est 0. Définissez-le sur 1 pour obtenir le résultat MATLAB:
>>> np.std([1,3,4,6], ddof=1)
2.0816659994661326
Pour ajouter un peu plus de contexte, dans le calcul de la variance (dont l'écart-type est la racine carrée), nous divisons généralement par le nombre de valeurs que nous avons.
Mais si nous sélectionnons un échantillon aléatoire d'éléments N à partir d'une distribution plus grande et calculons la variance, la division par N peut conduire à une sous-estimation de la variance réelle. Pour résoudre ce problème, nous pouvons réduire le nombre on divise par (degrés de liberté) pour un nombre inférieur à N (généralement N-1). Le paramètre ddof nous permet de changer le diviseur par le montant que nous spécifions.
Sauf indication contraire, NumPy calculera l'estimateur biaisé pour la variance (ddof=0, en divisant par N). C'est ce que vous voulez si vous travaillez avec toute la distribution (et non un sous-ensemble de valeurs qui ont été choisies au hasard à partir d'une distribution plus grande). Si le paramètre ddof est donné, NumPy se divise par N - ddof à la place.
Le comportement par défaut de std de MATLAB est de corriger le biais de la variance de l'échantillon en divisant par N-1. Cela élimine une partie (mais probablement pas la totalité) du biais dans l'écart-type. C'est probablement ce que vous voulez si vous utilisez la fonction sur un échantillon aléatoire d'une distribution plus grande.
La belle réponse de @ hbaderts donne d'autres détails mathématiques.
, L'écart type est la racine carrée de la variance. La variance d'une variable aléatoire X est défini comme
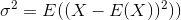
Un estimateur de la variance serait donc
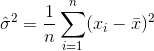
Où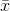 
désigne la moyenne de l'échantillon. Pour 
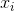sélectionné au hasard, on peut montrer que cet estimateur ne converge pas vers la variance réelle, mais vers
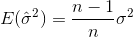
Si vous sélectionnez des échantillons au hasard et Estimez la moyenne et la variance de l'échantillon, vous utiliser un estimateur corrigé (non biaisé)
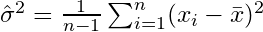
Qui convergera vers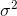 
. Le terme de correction 
est aussi appelé correction de Bessel.
Maintenant, par défaut, MATLABs std calcule la impartiale estimateur avec le terme de correction n-1. NumPy cependant (comme l'a expliqué @ ajcr) calcule l'estimateur biaisé Sans terme de correction par défaut. Le paramètre ddof permet de définir n'importe quel terme de correction n-ddof. En le définissant sur 1 vous obtenez le même résultat que dans MATLAB.
De même, MATLAB permet d'ajouter un second paramètre w, qui spécifie le "schéma de pesage". La valeur par défaut, w=0, entraîne le terme de correction n-1 (estimateur non biaisé), tandis que pour w=1, seul n est utilisé comme terme de correction (estimateur biaisé).
Pour les personnes qui ne sont pas géniales avec les statistiques, un guide simpliste est:
Include
ddof=1si vous calculeznp.std()pour un échantillon tiré de votre ensemble de données complet.-
Assurez-vous que
ddof=0Si vous calculeznp.std()pour la population complète
Le DDOF est inclus pour les échantillons afin de contrebalancer le biais qui peut se produire dans les nombres.