Pourquoi dois-je appliquer une fonction de fenêtre d'échantillons lors de la construction d'un spectre de puissance d'un signal audio?
j'ai trouvé plusieurs fois le suivre les directives pour obtenir le spectre de puissance d'un signal audio:
- rassembler les N échantillons, où N est une puissance de 2
- appliquer une fonction de fenêtre appropriée aux échantillons, p.ex. Hanning
- passer les échantillons fendus à une routine FFT-idéalement, vous voulez un FFT réel à complexe mais si tout ce que vous avez est un FFT complexe à complexe alors passer 0 pour toute l'entrée imaginaire pièces
- calculez la grandeur au carré de vos bacs de sortie FFT (re * re + im * im)
- (optionnel) calculer 10 * log10 de chaque sortie au carré de magnitude pour obtenir une valeur de magnitude en dB
- maintenant que vous avez votre spectre de puissance, vous avez juste besoin d'identifier le(s) pic (s), ce qui devrait être assez simple si vous avez un rapport s/n raisonnable. Notez que la résolution de fréquence s'améliore avec un N. plus grand pour l'exemple ci-dessus de 44,1 kHz taux d'échantillonnage et N = 32768 la résolution de fréquence de chaque série est de 44100 / 32768 = 1,35 Hz.
Mais... pourquoi dois-je appliquer une fonction de fenêtre pour les échantillons? Qu'est que cela signifie vraiment?
Quel est le spectre de puissance, est-il de la puissance de chaque fréquence dans la gamme de fréquence d'échantillonnage? (exemple: visualiseur de son Windows media player?)
4 réponses
comme le dit @cyco130, vos échantillons sont déjà empilés par une fonction rectangulaire. Étant donné qu'une transformation de Fourier suppose une périodicité, toute discontinuité entre le dernier échantillon et le premier échantillon répété provoquera des artefacts dans le spectre (p. ex. "écaillage" des pics). Ceci est connu comme fuite spectrale. Pour réduire l'effet de ceci, nous appliquons une fonction de fenêtre effilée telle qu'un Hann fenêtre qui lisse une telle discontinuité et réduit ainsi artéfacts dans le spectre.
la plupart des signaux audio du monde réel ne sont pas périodiques, ce qui signifie que les signaux audio réels ne se répètent généralement pas exactement, sur une période de temps donnée.
cependant, le calcul de la transformation de Fourier suppose que le signal en cours de transformation de Fourier est périodique au cours de la période en question.
cette inadéquation entre l'hypothèse de la périodicité de Fourier et le fait réel que les signaux audio sont généralement non périodiques, conduit à des erreurs dans le transformer.
ces erreurs sont appelées "fuites spectrales", et se manifestent généralement comme une distribution erronée de l'énergie à travers le spectre de puissance du signal.
le graphique ci-dessous montre un gros plan du spectre de puissance d'une guitare acoustique jouant de la note A4. Le spectre a été calculé avec le FFT (transformée de Fourier rapide), mais le signal n'a pas été coupé avant le FFT.
remarquez la distribution de l'énergie au-dessus de la ligne de -60 dB, et les trois pics distincts à environ 440 Hz, 880 Hz et 1320 Hz. Cette distribution particulière d'énergie contient des erreurs de "fuite spectrale".
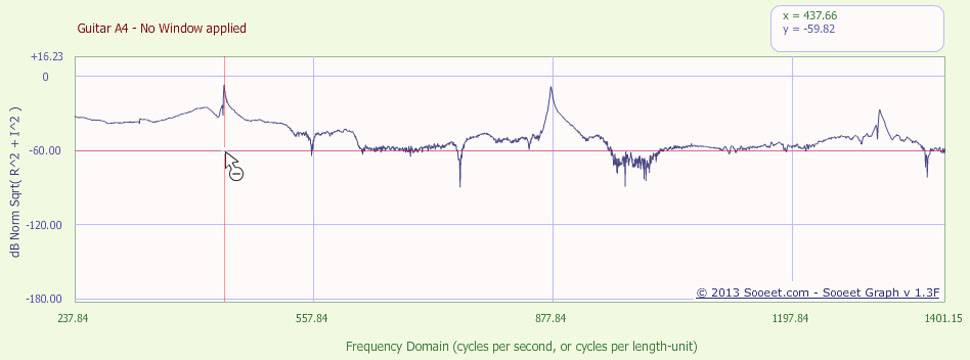
pour atténuer quelque peu les erreurs de "fuite spectrale", vous pouvez pré-multiplier le signal par une fonction de fenêtre spécialement conçue à cet effet, comme par exemple la fonction de fenêtre Hann.
le graphique ci-dessous montre la fonction Hann window dans le domaine time. Remarquez comment les queues de la fonction vont douceur de zéro, tandis que la partie centrale de la fonction tend douceur vers la valeur 1.
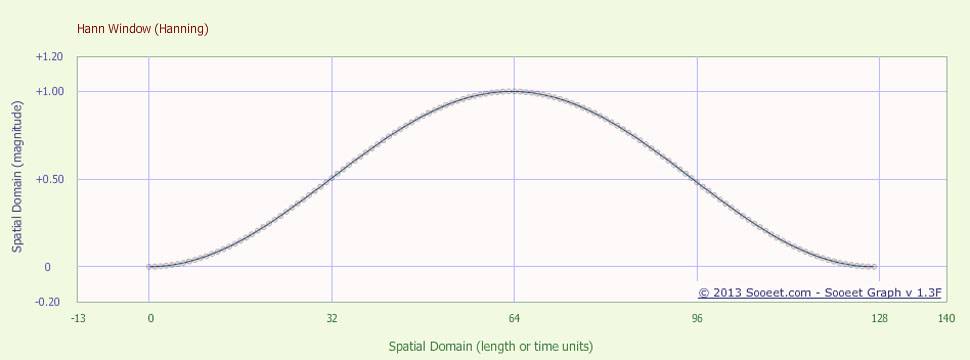
maintenant appliquons la fenêtre Hann aux données audio de la guitare, puis FFT le signal résultant.
le graphique ci-dessous montre un gros plan du spectre de puissance du même signal (une guitare acoustique jouant la note A4), mais cette fois le signal a été pré-multiplié par la fonction de fenêtre de Hann avant le FFT.
remarquez comment le la distribution de l'énergie au-dessus de la ligne de -60 dB a changé de façon significative, et la façon dont les trois pics distincts ont changé de forme et de hauteur. Cette distribution particulière de l'énergie spectrale contient moins d'erreurs de" fuite spectrale".
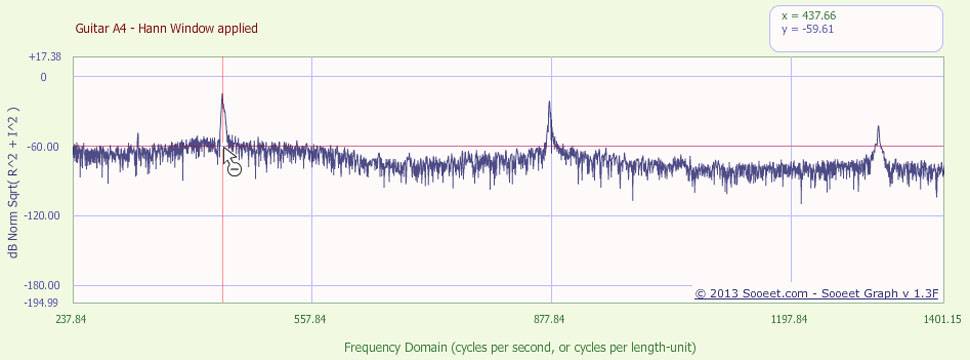
la note A4 de la guitare acoustique utilisée pour cette analyse a été échantillonnée à 44,1 KHz avec un microphone de haute qualité dans des conditions de studio, elle contient essentiellement zéro bruit de fond, aucun autre instrument ou voix, et aucun le post-traitement.
Références:
Real audio du signal de données, Hann fonction de fenêtre, les intrigues, la FFT, et l'analyse spectrale ont été fait ici:
transformée de Fourier rapide, Analyse spectrale, fonction de fenêtre de Hann, données audio
notez qu'une fenêtre non rectangulaire présente à la fois des avantages et des coûts. Le résultat d'une fenêtre dans le domaine du temps est équivalent à une convolution de la transformation de la fenêtre avec le spectre du signal. Une fenêtre typique, telle qu'une fenêtre de von Hann, réduira la " fuite "de tout contenu spectral non périodique, ce qui se traduira par un spectre moins bruyant; mais, en retour, la convolution" brouillera " n'importe quel pic spectral exactement ou proche de périodique à travers quelques bacs adjacents. par exemple, tous les les pics spectraux deviendront plus ronds, ce qui pourrait réduire la précision de l'estimation de la fréquence. Si vous savez, apriori, qu'il n'y a pas de contenu non périodique (par exemple, des données provenant d'un système d'échantillonnage synchrone en rotation), une fenêtre non rectangulaire pourrait en fait donner une image pire de FFT.
une fenêtre non rectangulaire est aussi un processus de perte informationnelle. Une quantité importante d'information spectrale près des bords de la fenêtre sera jetée, en supposant arithmétique de précision finie. Ainsi, les fenêtres non rectangulaires sont mieux utilisées avec le traitement de fenêtre qui se chevauchent, et / ou quand on peut supposer que le spectre d'intérêt est soit stationnaire à travers toute la largeur de la fenêtre, ou centré dans la fenêtre.
si vous n'appliquez aucune fonction de fenêtrage, vous appliquez en fait une fonction de fenêtrage rectangulaire. Différentes fonctions de fenêtrage ont des caractéristiques différentes, cela dépend de ce que vous voulez exactement.