Pourquoi les nombres à virgule flottante ont signé des zéros?
pourquoi les doubles ont -0 aussi bien que +0 ? Quel est le contexte et la signification?
4 réponses
-0 est (en général) est traitée comme 0 *******. Il peut en résulter quand un négatif nombre de virgule flottante est si proche de zéro qu'il peut être considéré comme 0 (pour être clair, je me réfère à sous-flux arithmétique , et les résultats des calculs suivants sont interprétés comme étant exactement "15191990920" , pas seulement des nombres vraiment petits). par exemple
System.out.println(-1 / Float.POSITIVE_INFINITY);
-0.0
si nous considérons le même cas avec un positif , nous recevrons notre bon vieux 0 :
System.out.println(1 / Float.POSITIVE_INFINITY);
0.0
******* voici un cas où l'utilisation de -0.0 résulte en quelque chose de différent que lors de l'utilisation de 0.0 :
System.out.println(1 / 0.0);
System.out.println(1 / -0.0);
Infinity -Infinity
cela a du sens si nous considérons la fonction 1 / x . Comme x approches 0 de la + -côté, nous devrions obtenir positif infini, mais comme il approche de la - -côté, nous devrions obtenir négatif infini. Le graphique de la fonction doit le montrer clairement:
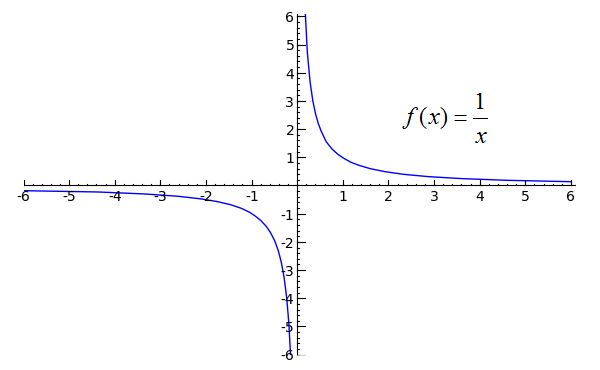
( source )
en mathématiques:
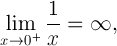
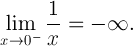
cela illustre une différence significative entre 0 et -0 au sens informatique.
voici quelques ressources pertinentes, dont certaines ont déjà été évoquées. J'ai inclus pour l'amour de exhaustivité:
- article Wikipedia sur le zéro signé
- "Ce que Chaque Ordinateur Scientifique Doit Savoir à Propos de l'Arithmétique à virgule Flottante" (Voir Signé section Zéro)
- (PDF) "Beaucoup de bruit pour Rien du Bit de Signe" - un document intéressant par W. Kahan.
De Wikipedia
zéro signé est zéro avec un signe associé. En arithmétique ordinaire,
−0 = +0 = 0. En informatique, existe le concept de existence de deux zéros dans les représentations de certains nombres, habituellement dénoté par−0et '+0", représentant négatif zéro et+0zéro positif , respectivement ( source ).cela se produit dans le signe et la magnitude et le complément de l'un signé représentations de nombre pour les entiers, et dans la plupart des points flottants représentations numériques. Le nombre 0 est généralement codé comme +0, mais peut être représenté par +0 ou -0.
selon le
IEEE 754 standard, zéro négatif et zéro positif si compare comme égal avec la comparaison (numérique) habituelle opérateurs, comme les opérateurs == de C et Java. ( source ).
quand vous avez un opération flottante qui produit un résultat qui est un point flottant négatif nombre proche de zéro , mais qui peut ne pas être représenté (dans le calcul) il est produire un"-0.0". Par exemple - 5.0 / Float.POSITIVE_INFINITY -> -0.0 .
This distinguer, dans -0.0 , et +0.0 , vous donne plus d'informations que simplement vous donner un résultat final 0. Bien sûr, ce concept il" seulement " existe dans un système de représentation fini comme celui utilisé dans les ordinateurs. En mathématiques, vous pouvez représenter n'importe quel nombre, même si elle est très très proche de zéro.
−0 et +0 sont le résultat d'opérations qui provoquent des underflows , du genre −00 ou +00 sont le résultat d'opérations qui causent débordement . Pour les opérations qui causent mathématiquement indetermination le résultat ins NaN (par exemple 0/0).
Quelle est la différence entre -0,0 et 0,0?
en réalité les deux sont représentés 0. De plus, (-0.0 = = 0.0) retourne vrai . Néanmoins:
1) 1/-0.0 produit - Infinity tandis que 1/0.0 produit Infinity .
2) 3 * (+0) = +0 et +0/-3 = -0 . Le règles de signe est applicable, lors de l'exécution de multiplications ou de division sur un zéro signé.
lecture obligatoire " Ce que Chaque Ordinateur Scientifique Doit Savoir à Propos de l'Arithmétique à virgule Flottante " (suggérer dans les commentaires).
voir la section "signé zéro" dans ce que tout informaticien devrait savoir sur L'arithmétique à virgule flottante
les zéros dans Java float et double ne représentent pas seulement le vrai zéro. Ils sont également utilisés comme résultat pour tout calcul dont le résultat exact a une magnitude trop faible pour être représenté. Il y a une grande différence, dans de nombreux contextes, entre dépassement de capacité d'un nombre négatif et dépassement de capacité d'un nombre positif. Par exemple, si x est un nombre positif de très faible magnitude, 1/x devrait être l'infini positif et 1/(-x) devrait être l'infini négatif. Le zéro signé préserve le signe des résultats de sous-flux.
la référence canonique pour l'utilité des zéros signés en virgule flottante est le papier de Kahan " coupures de branche pour les fonctions élémentaires complexes, ou beaucoup de bruit au sujet de rien signe Bit " (et certains de ses exposés sur le sujet).
la version courte est que dans les applications d'ingénierie raisonnablement courantes, l'information de signe qui est conservée par avoir signé Zéro est nécessaire pour obtenir des solutions correctes des méthodes numériques. Le signe de zero a peu de signification pour la plupart des opérations réelles , mais lorsque des fonctions à valeur complexe sont considérées, ou des mappages conformes sont utilisés, le signe de zero peut soudainement devenir tout à fait Critique.
Il est également intéressant de noter que l'original (1985) IEEE-754 le comité a examiné, et rejeté, de soutenir une projectif mode pour les opérations à virgule flottante, en vertu de laquelle il n'y aurait qu'un seul infini (+/-0 serait sémantiquement identique dans un tel mode, donc même s'il y avait encore deux codages, il n'y aurait qu'un seul zéro aussi bien).