Pourquoi DFS et non BFS pour trouver le cycle dans les graphiques

profondeur première recherche est plus efficace de mémoire que Largeur première recherche comme vous pouvez revenir en arrière plus tôt. Il est également plus facile à implémenter si vous utilisez la pile d'appels, mais cela dépend du chemin le plus long qui ne déborde pas la pile.

aussi si votre graphe est dirigé alors vous devez non seulement vous rappeler si vous avez visité un noeud ou non, mais aussi comment vous y êtes arrivé. Autrement vous pourriez penser que vous avez trouvé un cycle mais en réalité tout ce que vous avez est deux chemins séparés A - > B mais cela ne signifie pas qu'il y a un chemin B - > A. Exemple,

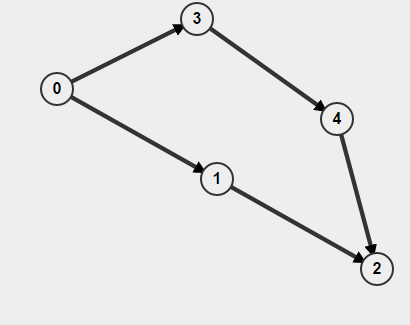
si vous faites BFS à partir de 0 , il détectera que le cycle est présent, mais en fait il n'y a pas de cycle.

avec une première recherche en profondeur, vous pouvez marquer les noeuds aussi visités que vous descendez et les dé-marquer que vous faites marche arrière. Voir les commentaires pour une amélioration de la performance sur cet algorithme.

pour le meilleur algorithme pour détecter les cycles dans un graphique dirigé vous pouvez regarder algorithme de Tarjan .

1. DFS est plus facile à mettre en œuvre
2. une fois que DFS trouve un cycle, la pile contient les noeuds formant le cycle. Le même n'est pas vrai pour BFS, donc vous devez faire un travail supplémentaire si vous voulez aussi imprimer le cycle trouvé. Cela rend DFS beaucoup plus pratique.

un BFS pourrait être raisonnable si le graphe n'est pas dirigé (soyez mon invité à montrer un algorithme efficace en utilisant BFS qui rapporterait les cycles dans un graphe dirigé!), où chaque "arête transversale" définit un cycle. Si le bord transversal est {v1, v2} , et la racine (dans l'arbre BFS) qui contient ces noeuds est r , alors le cycle est r ~ v1 - v2 ~ r ( ~ est un chemin, - un bord simple), qui peut être rapporté presque aussi facilement que dans DFS.

le la seule raison d'utiliser un BFS serait si vous savez que votre graphique (non dirigé) va avoir de longs chemins et un petit chemin couvert (en d'autres termes, profond et étroit). Dans ce cas, BFS aurait besoin proportionnellement moins de mémoire pour sa file d'attente que la pile de DFS (toutes deux toujours linéaires bien sûr).

dans tous les autres cas, la DSV est clairement la gagnante. il fonctionne à la fois sur des graphiques dirigés et non dirigés, et il est trivial de rapporter les cycles-il suffit de concatter n'importe quel bord arrière à le chemin de l'ancêtre au descendant, et vous obtenez le cycle. Dans l'ensemble, beaucoup mieux et pratique que BFS pour ce problème.

si vous placez un cycle à un endroit aléatoire dans un arbre, DFS aura tendance à frapper le cycle quand il est couvert environ la moitié de l'arbre, et la moitié du temps, il aura déjà traversé où le cycle va, et la moitié du temps, il ne sera pas (et le trouvera en moyenne dans la moitié du reste de l'arbre), de sorte qu'il évaluera en moyenne environ 0.5*0.5 + 0.5*0.75 = 0,625 de l'arbre.

Si vous placez un cycle à un endroit aléatoire dans un arbre, BFS aura tendance à frapper le cycle seulement quand il est évalué la couche de l'arbre à cette profondeur. Ainsi, vous finissent généralement par avoir à évaluer les feuilles d'un équilibre arbre binaire, ce qui permet généralement d'évaluer plus de l'arbre. En particulier, 3/4 du temps au moins un des deux liens apparaissent dans les feuilles de l'arbre, et sur ces cas, vous devez évaluer en moyenne 3/4 de l'arbre (s'il ya un lien) ou 7/8 de l'arbre (s'il ya deux), de sorte que vous êtes déjà à la hauteur d'une attente de recherche 1/2*3/4 + 1/4*7/8 = (7+12)/32 = 21/32 = 0,656... de l'arbre sans même ajouter le coût de la recherche d'un arbre avec un cycle ajouté loin des noeuds de feuilles.

en outre, DFS est plus facile à mettre en œuvre que BFS. Donc c'est celui à utiliser à moins que vous ne sachiez quelque chose sur vos cycles (par exemple les cycles sont susceptibles d'être près de la racine à partir de laquelle vous recherchez, à quel point BFS vous donne un avantage).

BFS l'habitude de travailler pour un graphe orienté dans la recherche de cycles. Considérons A - > B et A->C->B comme des chemins de A à B dans un graphique. BFS dira qu'après avoir suivi l'un des chemins que B est visité. En continuant à parcourir le chemin suivant,il dira que le noeud B marqué a été retrouvé, donc, il y a un cycle. Clairement il n'y a pas de cycle ici.

pour prouver qu'un graphe est cyclique, vous avez juste besoin de prouver qu'il a un cycle(bord pointant vers lui-même directement ou indirectement).

dans DFS nous prenons un sommet à la fois et vérifions s'il a un cycle. Dès qu'un cycle est trouvé, nous pouvons omettre de vérifier d'autres sommets.

dans BFS nous avons besoin de garder la trace de nombreux bords de sommet simultanément et le plus souvent qu'à la fin vous découvrez si elle a cycle. Lorsque la taille du graphique augmente BFS nécessite plus d'espace, de calcul et de temps par rapport à la DFS.

Ça dépend si vous parlez récursive ou itérative implémentations.

récursif-DFS visite chaque nœud deux fois. Iterative-BFS visite chaque noeud une fois.

si vous voulez détecter un cycle, vous devez enquêter sur les noeuds avant et après avoir ajouté leurs adjonctions -- à la fois quand vous" commencez "sur un noeud et quand vous" finissez " avec un noeud.

cela nécessite plus de travail itératif-BFS donc la plupart des gens choisissez Recursive-DFS.

notez qu'une simple implémentation de Iterative-DFS avec, disons, std::stack a le même problème que Iterative-bfs. Dans ce cas, vous devez placer des éléments factices dans la pile pour suivre lorsque vous "finissez" de travailler sur un noeud.

voir cette réponse pour plus de détails sur la façon itérative-DFS nécessite un travail supplémentaire pour déterminer quand vous "terminer" avec un noeud (répondu dans le contexte de TopoSort):

Tri topologique en utilisant DFS sans récursion

J'espère que cela explique pourquoi les gens préfèrent récursive-DFS pour les problèmes où vous devez déterminer quand vous "finissez" le traitement d'un noeud.