Quelle est l'erreur de numpy.polyfit?

Si vous spécifiez full=True dans votre polyfit, il va inclure des informations supplémentaires:

>>> x = np.arange(100)
>>> y = x**2 + 3*x + 5 + np.random.rand(100)
>>> np.polyfit(x, y, 2)
array([ 0.99995888,  3.00221219,  5.56776641])
>>> np.polyfit(x, y, 2, full=True)
(array([ 0.99995888,  3.00221219,  5.56776641]), # coefficients
 array([ 7.19260721]), # residuals
 3, # rank
 array([ 11.87708199,   3.5299267 ,   0.52876389]), # singular values
 2.2204460492503131e-14) # conditioning threshold

La valeur résiduelle retournée est la somme des carrés de l'ajustement des erreurs, vous ne savez pas si c'est ce que vous êtes après:

>>> np.sum((np.polyval(np.polyfit(x, y, 2), x) - y)**2)
7.1926072073491056

dans la version 1.7 il y a aussi un cov mot-clé qui renvoie la matrice de covariance pour vos coefficients, que vous pouvez utiliser pour calculer l'incertitude des coefficients d'ajustement eux-mêmes.

Comme vous pouvez le voir dans le documentation:

Returns
-------
p : ndarray, shape (M,) or (M, K)
    Polynomial coefficients, highest power first.
    If `y` was 2-D, the coefficients for `k`-th data set are in ``p[:,k]``.

residuals, rank, singular_values, rcond : present only if `full` = True
    Residuals of the least-squares fit, the effective rank of the scaled
    Vandermonde coefficient matrix, its singular values, and the specified
    value of `rcond`. For more details, see `linalg.lstsq`.

ce Qui signifie que si vous pouvez faire un ajustement et d'obtenir les résidus que:

 import numpy as np
 x = np.arange(10)
 y = x**2 -3*x + np.random.random(10)

 p, res, _, _, _ = numpy.polyfit(x, y, deg, full=True)

p sont vos paramètres d'ajustement, et l' res seront les résidus, comme décrit ci-dessus. _'s sont parce que vous n'avez pas besoin de sauver les trois derniers paramètres, donc vous pouvez juste les sauver dans la variable _ que vous n'utiliserez pas. C'est une convention et n'est pas requis.

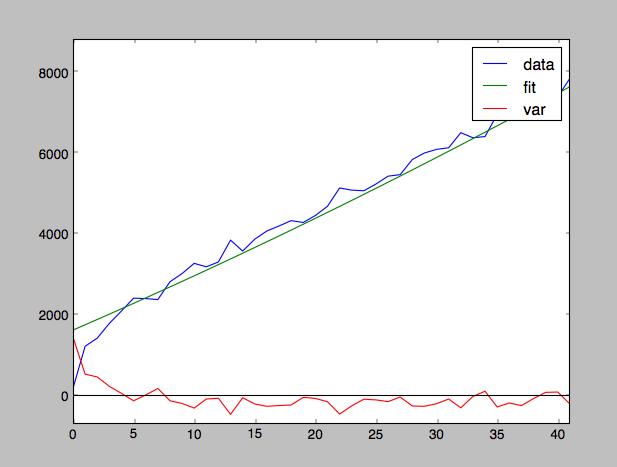
la réponse de@Jaime explique ce que signifie le résidu. Une autre chose que vous pouvez faire est de regarder ces déviations au carré comme une fonction (dont la somme est res). Cela est particulièrement utile pour déceler une tendance qui ne convenait pas suffisamment. res peut être important en raison du bruit statistique, ou peut-être un mauvais ajustement systématique, par exemple:

x = np.arange(100)
y = 1000*np.sqrt(x) + x**2 - 10*x + 500*np.random.random(100) - 250

p = np.polyfit(x,y,2) # insufficient degree to include sqrt

yfit = np.polyval(p,x)

figure()
plot(x,y, label='data')
plot(x,yfit, label='fit')
plot(x,yfit-y, label='var')

ainsi, dans la figure, noter la mauvaise ajustement près de x = 0: