Quelle est la différence entre pandas ACF et statsmodel ACF?

Je calcule la fonction D'autocorrélation pour les retours d'actions. Pour ce faire, j'ai testé deux fonctions, l' autocorr fonction intégrée dans Pandas, et le acf fonction fournie par statsmodels.tsa. Ceci est fait dans le suivant MWE:

import pandas as pd
from pandas_datareader import data
import matplotlib.pyplot as plt
import datetime
from dateutil.relativedelta import relativedelta
from statsmodels.tsa.stattools import acf, pacf

ticker = 'AAPL'
time_ago = datetime.datetime.today().date() - relativedelta(months = 6)

ticker_data = data.get_data_yahoo(ticker, time_ago)['Adj Close'].pct_change().dropna()
ticker_data_len = len(ticker_data)

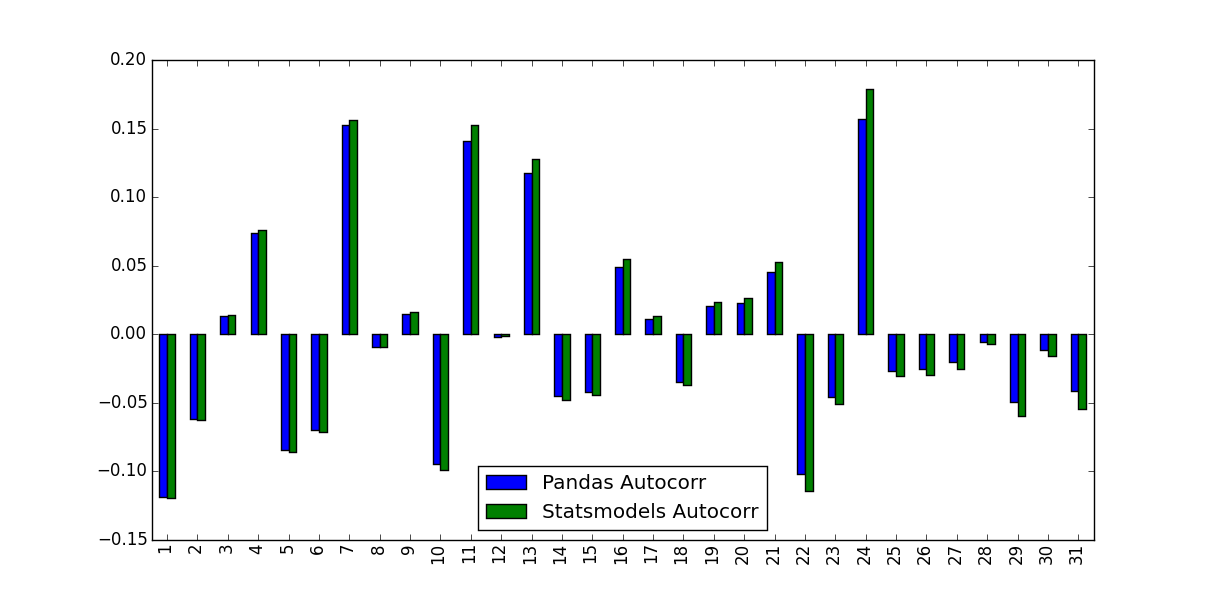
ticker_data_acf_1 =  acf(ticker_data)[1:32]
ticker_data_acf_2 = [ticker_data.autocorr(i) for i in range(1,32)]

test_df = pd.DataFrame([ticker_data_acf_1, ticker_data_acf_2]).T
test_df.columns = ['Pandas Autocorr', 'Statsmodels Autocorr']
test_df.index += 1
test_df.plot(kind='bar')

ce que j'ai remarqué, c'est que les valeurs prédites n'étaient pas identiques:

enter image description here

quelles sont les raisons de cette différence et quelles sont les valeurs à utiliser?

15
demandé sur BML91 2016-03-16 17:43:08

2 réponses

la différence entre la version Pandas et la version Statsmodels réside dans la soustraction moyenne et la normalisation / Division de la variance:

  • autocorr ne fait rien de plus que de passer des sous-séries de la série originale à np.corrcoef. Dans cette méthode, la moyenne de l'échantillon et la variance de l'échantillon de ces sous-séries sont utilisées pour déterminer le coefficient de corrélation
  • acf, au contraire, utilise la moyenne globale de l'échantillon de la série et la variance de l'échantillon pour déterminer la corrélation coefficient.

les différences peuvent devenir plus petites pour les séries chronologiques plus longues, mais sont assez grandes pour les séries plus courtes.

par rapport à Matlab, les Pandas autocorr la fonction correspond probablement à faire des Matlabs xcorr (cross-corr) avec la série (décalée) elle-même, au lieu deautocorr, qui calcule l'autocorrélation de l'échantillon (en devinant à partir du docs; Je ne peux pas valider cela parce que je n'ai pas accès à Matlab).

voir ce MWE pour clarification:

import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import acf
import matplotlib.pyplot as plt
plt.style.use("seaborn-colorblind")

def autocorr_by_hand(x, lag):
    # Slice the relevant subseries based on the lag
    y1 = x[:(len(x)-lag)]
    y2 = x[lag:]
    # Subtract the subseries means
    sum_product = np.sum((y1-np.mean(y1))*(y2-np.mean(y2)))
    # Normalize with the subseries stds
    return sum_product / ((len(x) - lag) * np.std(y1) * np.std(y2))

def acf_by_hand(x, lag):
    # Slice the relevant subseries based on the lag
    y1 = x[:(len(x)-lag)]
    y2 = x[lag:]
    # Subtract the mean of the whole series x to calculate Cov
    sum_product = np.sum((y1-np.mean(x))*(y2-np.mean(x)))
    # Normalize with var of whole series
    return sum_product / ((len(x) - lag) * np.var(x))

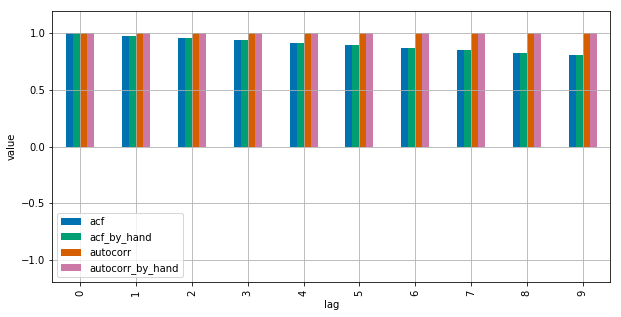
x = np.linspace(0,100,101)

results = {}
nlags=10
results["acf_by_hand"] = [acf_by_hand(x, lag) for lag in range(nlags)]
results["autocorr_by_hand"] = [autocorr_by_hand(x, lag) for lag in range(nlags)]
results["autocorr"] = [pd.Series(x).autocorr(lag) for lag in range(nlags)]
results["acf"] = acf(x, unbiased=True, nlags=nlags-1)

pd.DataFrame(results).plot(kind="bar", figsize=(10,5), grid=True)
plt.xlabel("lag")
plt.ylim([-1.2, 1.2])
plt.ylabel("value")
plt.show()

enter image description here

Statsmodels utilise np.correlate pour optimiser ceci, mais c'est essentiellement comme ça que ça marche.

11
répondu nikhase 2018-06-18 15:01:24

Comme suggéré dans les commentaires, le problème peut être diminué, mais pas complètement résolu, en fournissant unbiased=Truestatsmodels fonction. À l'aide d'un aléatoire d'entrée:

import statistics

import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import acf

DATA_LEN = 100
N_TESTS = 100
N_LAGS = 32

def test(unbiased):
  data = pd.Series(np.random.random(DATA_LEN))
  data_acf_1 = acf(data, unbiased=unbiased, nlags=N_LAGS)
  data_acf_2 = [data.autocorr(i) for i in range(N_LAGS+1)]
  # return difference between results
  return sum(abs(data_acf_1 - data_acf_2))

for value in (False, True):
  diffs = [test(value) for _ in range(N_TESTS)]
  print(value, statistics.mean(diffs))

Sortie:

False 0.464562410987
True 0.0820847168593
0
répondu Marein 2017-07-21 17:52:27