Quel est le but de meshgrid en Python / NumPy?
quelqu'un Peut m'expliquer quel est le but de meshgrid fonction Numpy? Je sais que ça crée une sorte de grille de coordonnées pour tracer, mais je ne vois pas l'avantage direct de ça.
j'étudie "Python Machine Learning" DE Sebastian Raschka, et il l'utilise pour tracer les frontières de décision. Voir Entrée 11 ici .
j'ai également essayé ce code à partir de la documentation officielle, mais, encore une fois, la sortie n'a pas vraiment de sens pour moi.
x = np.arange(-5, 5, 1)
y = np.arange(-5, 5, 1)
xx, yy = np.meshgrid(x, y, sparse=True)
z = np.sin(xx**2 + yy**2) / (xx**2 + yy**2)
h = plt.contourf(x,y,z)
s'il vous plaît, si possible, aussi me montrer beaucoup d'exemples du monde réel.
5 réponses
Le but de meshgrid est de créer une grille rectangulaire de sortir d'un tableau de valeurs x et un tableau de valeurs de y.
Ainsi, par exemple, si nous voulons créer une grille où nous avons un point à chaque valeur entière entre 0 et 4 dans les deux directions x et y. Pour créer une grille rectangulaire, nous avons besoin de chaque combinaison des points x et y .
ça va faire 25 points, non? Donc, si nous voulions créer un x et y tableau pour tous ces points, nous pourrait faire ce qui suit.
x[0,0] = 0 y[0,0] = 0
x[0,1] = 1 y[0,1] = 0
x[0,2] = 2 y[0,2] = 0
x[0,3] = 3 y[0,3] = 0
x[0,4] = 4 y[0,4] = 0
x[1,0] = 0 y[1,0] = 1
x[1,1] = 1 y[1,1] = 1
...
x[4,3] = 3 y[4,3] = 4
x[4,4] = 4 y[4,4] = 4
Ce résultat suivant x et y matrices, telles que le couplage de l'élément correspondant dans chaque matrice donne les coordonnées x et y d'un point dans la grille.
x = 0 1 2 3 4 y = 0 0 0 0 0
0 1 2 3 4 1 1 1 1 1
0 1 2 3 4 2 2 2 2 2
0 1 2 3 4 3 3 3 3 3
0 1 2 3 4 4 4 4 4 4
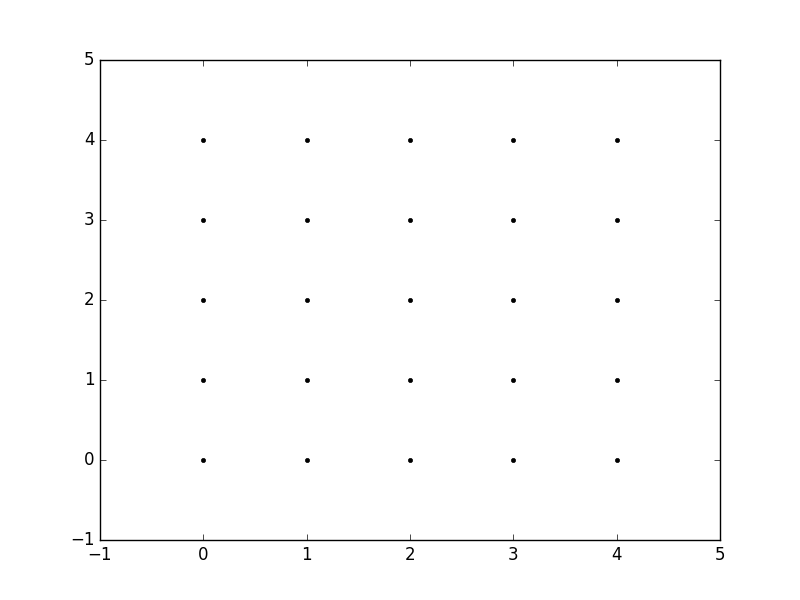
nous pouvons ensuite tracer ceux-ci pour vérifier qu'ils sont une grille:
plt.plot(x,y, marker='.', color='k', linestyle='none')
évidemment, cela devient très fastidieux surtout pour les grandes gammes de x et y . Au lieu de cela, meshgrid peut réellement générer ceci pour nous: tout ce que nous devons spécifier sont les valeurs uniques x et y .
xvalues = np.array([0, 1, 2, 3, 4]);
yvalues = np.array([0, 1, 2, 3, 4]);
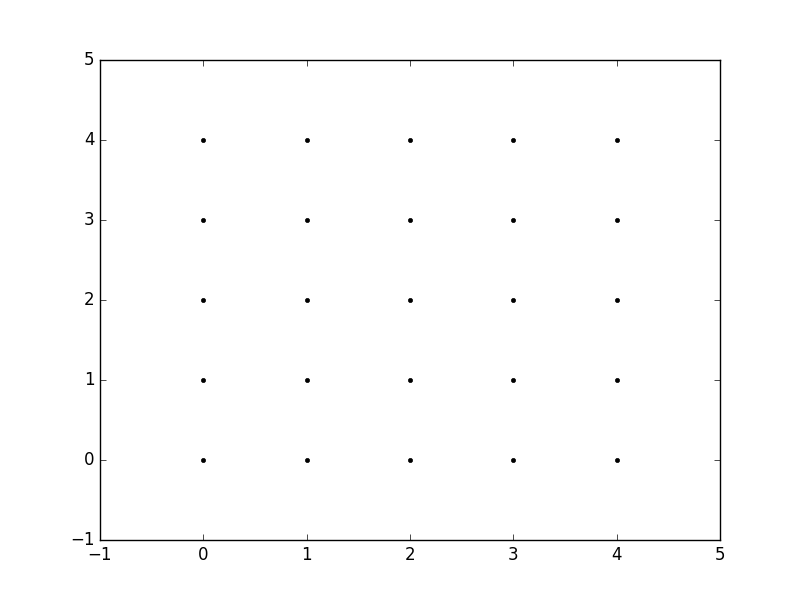
maintenant, quand nous appelons meshgrid , nous obtenons la sortie précédente automatiquement.
xx, yy = np.meshgrid(xvalues, yvalues)
plt.plot(xx, yy, marker='.', color='k', linestyle='none')
la Création de ces grilles rectangulaires est utile pour un certain nombre de tâches. Dans l'exemple que vous avez fourni dans votre post, c'est simplement une façon d'échantillonner une fonction ( sin(x**2 + y**2) / (x**2 + y**2) ) sur une plage de valeurs pour x et y .
parce que cette fonction a été échantillonnée sur une grille rectangulaire, la fonction peut maintenant être visualisée comme une"image".
en outre, le résultat peut maintenant être passé à des fonctions qui attendent des données sur la grille rectangulaire (i.e. contourf )
supposons que vous ayez une fonction:
def sinus2d(x, y):
return np.sin(x) + np.sin(y)
et vous voulez, par exemple, voir à quoi il ressemble dans la gamme de 0 à 2*pi. Comment le feriez-vous? Il y a np.meshgrid entre:
xx, yy = np.meshgrid(np.linspace(0,2*np.pi,100), np.linspace(0,2*np.pi,100))
z = sinus2d(xx, yy) # Create the image on this grid
et un tel complot ressemblerait à:
import matplotlib.pyplot as plt
plt.imshow(z, origin='lower', interpolation='none')
plt.show()
Donc np.meshgrid est juste une commodité. En principe, la même chose pourrait être fait par:
z2 = sinus2d(np.linspace(0,2*np.pi,100)[:,None], np.linspace(0,2*np.pi,100)[None,:])
mais là vous devez être conscient de vos dimensions (supposons que vous en ayez plus de deux ...) et le droit de radiodiffusion. np.meshgrid fait tout cela pour vous.
meshgrid vous permet également de supprimer les coordonnées avec les données si, par exemple, vous voulez faire une interpolation mais exclure certaines valeurs:
condition = z>0.6
z_new = z[condition] # This will make your array 1D
alors comment feriez-vous l'interpolation maintenant? Vous pouvez donner x et y à une fonction d'interpolation comme scipy.interpolate.interp2d donc vous avez besoin d'un moyen de savoir quelles coordonnées ont été supprimées:
x_new = xx[condition]
y_new = yy[condition]
et puis vous pouvez toujours interpoler avec le "droit" de coordonnées (essayer sans meshgrid et vous aurez beaucoup de code supplémentaire):
from scipy.interpolate import interp2d
interpolated = interp2(x_new, y_new, z_new)
et le meshgrid original vous permet d'obtenir l'interpolation sur la grille d'origine à nouveau:
interpolated_grid = interpolated(xx, yy)
ce ne sont que quelques exemples où j'ai utilisé le meshgrid il pourrait y avoir beaucoup plus.
en fait, le but de np.meshgrid est déjà mentionné dans la documentation:
matrices de coordonnées de retour des vecteurs de coordonnées.
Faire de N-D de coordonner les tableaux pour vectorisé évaluations de N-D scalaire/vectorielle des champs de plus de N-D des grilles, donné à une dimension de coordonner les tableaux x1, x2,..., xn.
donc son but premier est de créer des matrices de coordonnées.
vous vous êtes probablement demandé:
Pourquoi devons-nous créer des matrices de coordonnées?
la raison pour laquelle vous avez besoin de matrices de coordonnées avec Python/NumPy est qu'il n'y a pas de relation directe entre les coordonnées et les valeurs, sauf lorsque vos coordonnées commencent par zéro et sont des entiers purement positifs. Ensuite, vous pouvez simplement utiliser les indices d'un tableau comme index. Toutefois, lorsque ce n'est pas le cas, vous avez en quelque sorte besoin de stocker des coordonnées à côté de vos données. C'est là que les grilles entrent en jeu.
supposons que vos données soient:
1 2 1
2 5 2
1 2 1
Cependant chaque valeur représente une région de 2 kilomètres de large horizontalement et 3 kilomètres verticalement. Supposons que votre origine soit le coin supérieur gauche et vous voulez des tableaux qui représentent la distance que vous pourriez utiliser:
import numpy as np
h, v = np.meshgrid(np.arange(3)*3, np.arange(3)*2)
où h est:
0 2 4
0 2 4
0 2 4
et h:
0 0 0
3 3 3
6 6 6
donc si vous avez deux indices, disons x et y (c'est pourquoi la valeur de retour de meshgrid est habituellement xx ou xs au lieu de x dans ce cas j'ai choisi h pour horizontalement! ensuite, vous pouvez obtenir la coordonnée x du point, la coordonnée y du point et de la valeur à ce point en utilisant:
h[x, y] # horizontal coordinate
v[x, y] # vertical coordinate
data[x, y] # value
Cela rend beaucoup plus facile de garder la trace des coordonnées et (encore plus important) vous pouvez les passer à des fonctions qui ont besoin de connaître les coordonnées.
une explication un peu plus longue
Toutefois, np.meshgrid lui-même n'est pas souvent utilisé directement, souvent on utilise juste l'un des similaires objets np.mgrid ou np.ogrid .
Ici np.mgrid représente le sparse=False et np.ogrid le sparse=True cas (je me réfère à la sparse argument np.meshgrid ). Notez qu'il existe une différence significative entre
np.meshgrid et np.ogrid et np.mgrid : les deux premières valeurs retournées (s'il y en a deux ou plus) sont inversées. Souvent, cela n'a pas d'importance, mais vous devriez donner des noms de variables significatives
en fonction du contexte. Par exemple dans le cas d'une grille 2D et matplotlib.pyplot.imshow il est permis de nommer le premier article retourné de np.meshgrid x et le second y alors qu'il est
l'inverse pour np.mgrid et np.ogrid .
np.ogrid et réseaux épars
>>> import numpy as np
>>> yy, xx = np.ogrid[-5:6, -5:6]
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5],
[-4],
[-3],
[-2],
[-1],
[ 0],
[ 1],
[ 2],
[ 3],
[ 4],
[ 5]])
comme déjà dit la sortie est inversée par rapport à np.meshgrid , c'est pourquoi je l'ai déballé comme yy, xx au lieu de xx, yy :
>>> xx, yy = np.meshgrid(np.arange(-5, 6), np.arange(-5, 6), sparse=True)
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5],
[-4],
[-3],
[-2],
[-1],
[ 0],
[ 1],
[ 2],
[ 3],
[ 4],
[ 5]])
cela ressemble déjà à des coordonnées, en particulier le x et des lignes y pour les parcelles 2D.
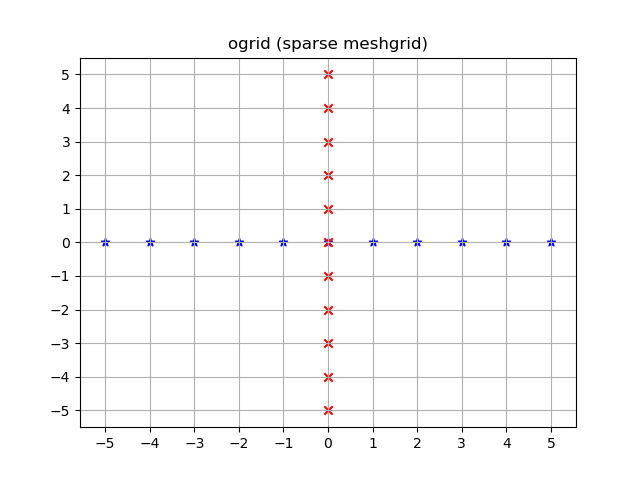
visualisé:
yy, xx = np.ogrid[-5:6, -5:6]
plt.figure()
plt.title('ogrid (sparse meshgrid)')
plt.grid()
plt.xticks(xx.ravel())
plt.yticks(yy.ravel())
plt.scatter(xx, np.zeros_like(xx), color="blue", marker="*")
plt.scatter(np.zeros_like(yy), yy, color="red", marker="x")
np.mgrid 1519900920"
>>> yy, xx = np.mgrid[-5:6, -5:6]
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5, -5, -5, -5, -5, -5, -5, -5, -5, -5, -5],
[-4, -4, -4, -4, -4, -4, -4, -4, -4, -4, -4],
[-3, -3, -3, -3, -3, -3, -3, -3, -3, -3, -3],
[-2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2],
[ 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3],
[ 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4],
[ 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]])
>>> yy, xx = np.mgrid[-5:6, -5:6]
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5, -5, -5, -5, -5, -5, -5, -5, -5, -5, -5],
[-4, -4, -4, -4, -4, -4, -4, -4, -4, -4, -4],
[-3, -3, -3, -3, -3, -3, -3, -3, -3, -3, -3],
[-2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2],
[ 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3],
[ 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4],
[ 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]])
la même chose s'applique ici: la sortie est inversée par rapport à np.meshgrid :
>>> xx, yy = np.meshgrid(np.arange(-5, 6), np.arange(-5, 6))
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5, -5, -5, -5, -5, -5, -5, -5, -5, -5, -5],
[-4, -4, -4, -4, -4, -4, -4, -4, -4, -4, -4],
[-3, -3, -3, -3, -3, -3, -3, -3, -3, -3, -3],
[-2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2],
[ 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3],
[ 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4],
[ 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]])
contrairement à ogrid ces tableaux contiennent tous xx et yy coordonnées dans le -5 <= xx <= 5; -5 <= yy <= 5 grille.
yy, xx = np.mgrid[-5:6, -5:6]
plt.figure()
plt.title('mgrid (dense meshgrid)')
plt.grid()
plt.xticks(xx[0])
plt.yticks(yy[:, 0])
plt.scatter(xx, yy, color="red", marker="x")
fonctionnalité
ce n'est pas seulement limité à la 2D, ces fonctions fonctionnent pour des dimensions arbitraires (bien, il y a un nombre maximum d'arguments donnés à la fonction en Python et un nombre maximum de dimensions que NumPy permet):
>>> x1, x2, x3, x4 = np.ogrid[:3, 1:4, 2:5, 3:6]
>>> for i, x in enumerate([x1, x2, x3, x4]):
... print('x{}'.format(i+1))
... print(repr(x))
x1
array([[[[0]]],
[[[1]]],
[[[2]]]])
x2
array([[[[1]],
[[2]],
[[3]]]])
x3
array([[[[2],
[3],
[4]]]])
x4
array([[[[3, 4, 5]]]])
>>> # equivalent meshgrid output, note how the first two arguments are reversed and the unpacking
>>> x2, x1, x3, x4 = np.meshgrid(np.arange(1,4), np.arange(3), np.arange(2, 5), np.arange(3, 6), sparse=True)
>>> for i, x in enumerate([x1, x2, x3, x4]):
... print('x{}'.format(i+1))
... print(repr(x))
# Identical output so it's omitted here.
même si cela fonctionne aussi pour 1D il y a deux (beaucoup plus commun) fonctions de création de grille 1D:
outre l'argument start et stop il soutient également l'argument step (même les étapes complexes qui représentent le nombre d'étapes):
>>> x1, x2 = np.mgrid[1:10:2, 1:10:4j]
>>> x1 # The dimension with the explicit step width of 2
array([[1., 1., 1., 1.],
[3., 3., 3., 3.],
[5., 5., 5., 5.],
[7., 7., 7., 7.],
[9., 9., 9., 9.]])
>>> x2 # The dimension with the "number of steps"
array([[ 1., 4., 7., 10.],
[ 1., 4., 7., 10.],
[ 1., 4., 7., 10.],
[ 1., 4., 7., 10.],
[ 1., 4., 7., 10.]])
Applications
vous avez spécifiquement demandé sur le but et en fait ces grilles sont extrêmement utiles si vous avez besoin d'un système de coordonnées.
par exemple si vous avez une fonction NumPy qui calcule la distance en deux dimensions:
def distance_2d(x_point, y_point, x, y):
return np.hypot(x-x_point, y-y_point)
Et vous voulez connaître la distance de chaque point:
>>> ys, xs = np.ogrid[-5:5, -5:5]
>>> distances = distance_2d(1, 2, xs, ys) # distance to point (1, 2)
>>> distances
array([[9.21954446, 8.60232527, 8.06225775, 7.61577311, 7.28010989,
7.07106781, 7. , 7.07106781, 7.28010989, 7.61577311],
[8.48528137, 7.81024968, 7.21110255, 6.70820393, 6.32455532,
6.08276253, 6. , 6.08276253, 6.32455532, 6.70820393],
[7.81024968, 7.07106781, 6.40312424, 5.83095189, 5.38516481,
5.09901951, 5. , 5.09901951, 5.38516481, 5.83095189],
[7.21110255, 6.40312424, 5.65685425, 5. , 4.47213595,
4.12310563, 4. , 4.12310563, 4.47213595, 5. ],
[6.70820393, 5.83095189, 5. , 4.24264069, 3.60555128,
3.16227766, 3. , 3.16227766, 3.60555128, 4.24264069],
[6.32455532, 5.38516481, 4.47213595, 3.60555128, 2.82842712,
2.23606798, 2. , 2.23606798, 2.82842712, 3.60555128],
[6.08276253, 5.09901951, 4.12310563, 3.16227766, 2.23606798,
1.41421356, 1. , 1.41421356, 2.23606798, 3.16227766],
[6. , 5. , 4. , 3. , 2. ,
1. , 0. , 1. , 2. , 3. ],
[6.08276253, 5.09901951, 4.12310563, 3.16227766, 2.23606798,
1.41421356, 1. , 1.41421356, 2.23606798, 3.16227766],
[6.32455532, 5.38516481, 4.47213595, 3.60555128, 2.82842712,
2.23606798, 2. , 2.23606798, 2.82842712, 3.60555128]])
la sortie serait identique si on passait dans une grille dense au lieu d'une grille ouverte. Num pys broadcasting rend cela possible!
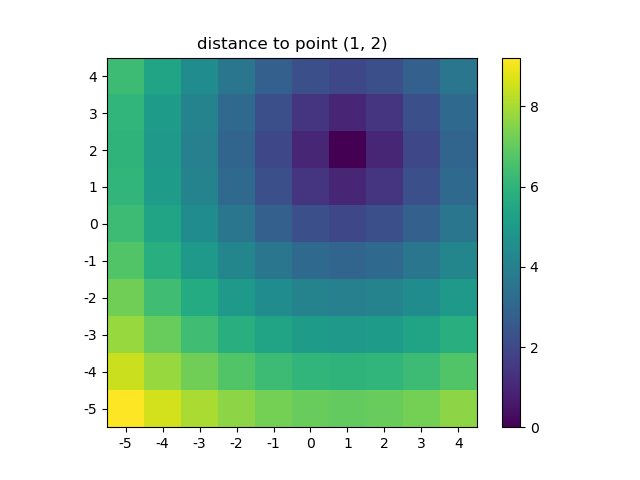
visualisons le résultat:
plt.figure()
plt.title('distance to point (1, 2)')
plt.imshow(distances, origin='lower', interpolation="none")
plt.xticks(np.arange(xs.shape[1]), xs.ravel()) # need to set the ticks manually
plt.yticks(np.arange(ys.shape[0]), ys.ravel())
plt.colorbar()
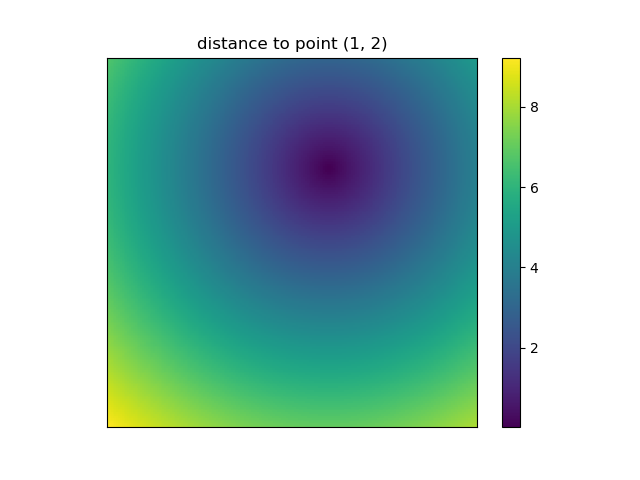
et c'est aussi le moment où NumPys mgrid et ogrid deviennent très pratiques, parce qu'il vous permet de changer facilement la résolution de vos grilles:
ys, xs = np.ogrid[-5:5:200j, -5:5:200j]
# otherwise same code as above
Cependant, puisque imshow ne supporte pas x et "1519230920 entrées" on doit changer les tiques à la main. Il serait vraiment pratique si elle accepterait de la x et y coordonnées, droit?
Il est facile d'écrire des fonctions avec NumPy qui traitent naturellement avec des grilles. En outre, il existe plusieurs fonctions de NumPy, SciPy, MatPlotLib qu'attendez vous pour passer dans la grille.
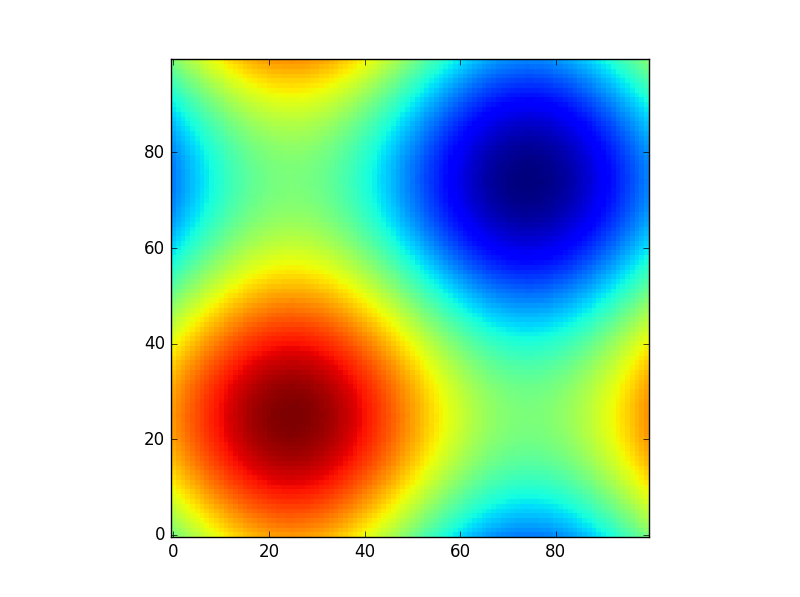
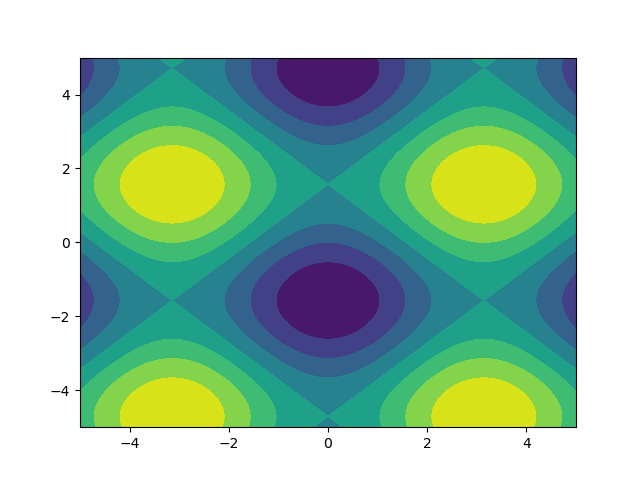
j'aime les images donc, nous allons explorer matplotlib.pyplot.contour :
ys, xs = np.mgrid[-5:5:200j, -5:5:200j]
density = np.sin(ys)-np.cos(xs)
plt.figure()
plt.contour(xs, ys, density)
Note la façon dont les coordonnées sont déjà correctement réglé! Ce ne serait pas le cas si vous venez de passer dans le density .
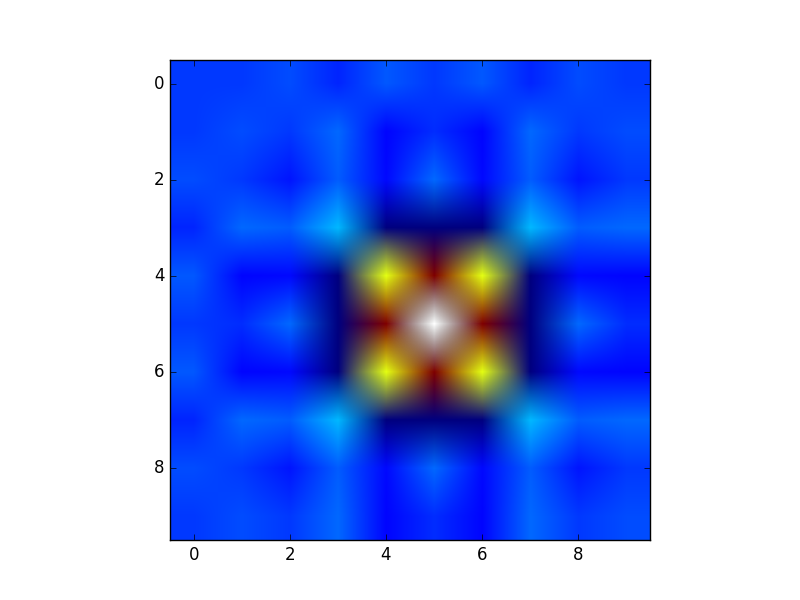
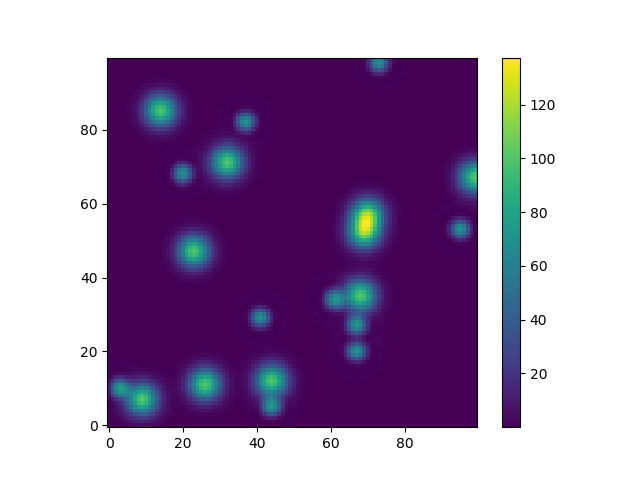
Ou pour donner un autre exemple amusant à l'aide de astropy modèles (cette fois, j'ai ne vous souciez pas beaucoup des coordonnées, je les utilise juste pour créer certains grille):
from astropy.modeling import models
z = np.zeros((100, 100))
y, x = np.mgrid[0:100, 0:100]
for _ in range(10):
g2d = models.Gaussian2D(amplitude=100,
x_mean=np.random.randint(0, 100),
y_mean=np.random.randint(0, 100),
x_stddev=3,
y_stddev=3)
z += g2d(x, y)
a2d = models.AiryDisk2D(amplitude=70,
x_0=np.random.randint(0, 100),
y_0=np.random.randint(0, 100),
radius=5)
z += a2d(x, y)
bien que ce soit juste "pour les looks" plusieurs fonctions liées aux modèles fonctionnels et l'ajustement (par exemple scipy.interpolate.interp2d ,
scipy.interpolate.griddata même montrer des exemples en utilisant np.mgrid ) en Scipy, etc. exiger des grilles. La plupart d'entre eux fonctionnent avec des grilles ouvertes et
les grilles denses, cependant certains ne fonctionnent qu'avec l'un d'eux.
meshgrid aide à créer une grille rectangulaire à partir de deux tableaux 1-D de toutes les paires de points des deux tableaux.
x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 1, 2, 3, 4])
maintenant, si vous avez défini une fonction f (x, y) et que vous voulez appliquer cette fonction à toutes les combinaisons possibles de points des tableaux 'x' et 'y', alors vous pouvez faire ceci:
f(*np.meshgrid(x, y))
dire, si votre Fonction produit juste le produit de deux éléments, alors c'est comment un produit cartésien peut être atteint, efficace pour de grands tableaux.
Visée de ici