Qu'y a-t-il dans votre sac à outils Mathematica? [fermé]

L'une des bonnes choses au sujet de L'interface du bloc-notes Mathematica est qu'elle peut évaluer des expressions dans n'importe quelle Langue, pas seulement Mathematica. À titre d'exemple simple, envisagez de créer un nouveau type de cellule d'entrée Shell qui transmet l'expression contenue au shell du système d'exploitation pour évaluation.

tout d'abord, définissez une fonction qui délègue l'évaluation d'une commande textuelle au shell externe:

shellEvaluate[cmd_, _] := Import["!"~~cmd, "Text"]

le second argument est nécessaire et ignoré pour des raisons qui apparaîtront plus tard. Ensuite, nous voulons créer un nouveau style appelé Shell :

1. ouvrir un nouveau carnet.
2. sélectionnez l'élément de menu Format/Modifier la feuille de style...
3. dans le dialogue, à côté de entrez un nom de style: type Shell .
4. sélectionnez la case à côté du nouveau style.
5. sélectionner l'élément de menu Cell/Show Expression
6. remplace l'expression de la cellule par Étape 6 texte donnée ci-dessous.
7. une fois de plus, sélectionnez l'élément de menu Cell/Show Expression
8. fermez le dialogue.

utilisez la cellule suivante expression comme le Étape 6 texte :

Cell[StyleData["Shell"],
 CellFrame->{{0, 0}, {0.5, 0.5}},
 CellMargins->{{66, 4}, {0, 8}},
 Evaluatable->True,
 StripStyleOnPaste->True,
 CellEvaluationFunction->shellEvaluate,
 CellFrameLabels->{{None, "Shell"}, {None, None}},
 Hyphenation->False,
 AutoQuoteCharacters->{},
 PasteAutoQuoteCharacters->{},
 LanguageCategory->"Formula",
 ScriptLevel->1,
 MenuSortingValue->1800,
 FontFamily->"Courier"]

la plus grande partie de cette expression a été copiée directement sous forme de programme style. Les principaux changements sont les suivants:

 Evaluatable->True,
 CellEvaluationFunction->shellEvaluate,
 CellFrameLabels->{{None, "Shell"}, {None, None}},

Evaluatable permet la fonctionnalité SHIFT+ENTER pour la cellule. L'évaluation appellera CellEvaluationFunction en passant le contenu de la cellule et le type de contenu comme arguments ( shellEvaluate ignore ce dernier argument). CellFrameLabels est juste un concept qui laisse à l'utilisateur d'identifier que cette cellule est inhabituel.

avec tout cela en place, Nous pouvons maintenant entrer et évaluer une expression shell:

1. dans le bloc-notes créé dans les étapes ci-dessus, créer une cellule vide et sélectionner le support de la cellule.
2. sélectionnez l'élément du menu Format/Style/Shell .
3. Type valide shell du système d'exploitation de commande dans la cellule (par exemple " ls "sur Unix ou" dir " sur Windows).
4. Press SHIFT+ENTER.

il est préférable de conserver ce style défini dans une feuille de style située au centre. De plus, les fonctions d'évaluation telles que shellEvaluate sont mieux définies comme étant des talons en utilisant Déclarepackage dans init.m . Les détails de ces deux activités dépassent la portée de la présente réponse.

avec cette fonctionnalité, on peut créer des notebooks qui contiennent des expressions d'entrée dans n'importe quelle syntaxe d'intérêt. La fonction d'évaluation peut être écrite en Mathematica pur, ou déléguer une partie ou la totalité de l'évaluation à un organisme externe. Soyez conscient qu'il y a d'autres crochets qui se rapportent à l'évaluation des cellules, comme CellEpilog , CellProlog et CellDynamicExpression .

un modèle commun implique l'écriture de l'expression texte d'entrée à un fichier temporaire, la compilation du fichier dans une certaine langue, l'exécution de la programme et capturer la sortie pour écran ultime dans la cellule en sortie. Il y a beaucoup de détails à régler lors de la mise en œuvre d'une solution complète de ce genre (comme la saisie des messages d'erreur correctement), mais il faut comprendre le fait qu'il est non seulement possible de faire des choses comme ça, mais pratique.

sur une note personnelle, ce sont des fonctionnalités comme celle-ci qui font de l'interface de bloc-notes le centre de mon univers de programmation.

Mise à jour

la fonction d'aide suivante est utile pour créer de telles cellules:

evaluatableCell[label_String, evaluationFunction_] :=
  ( CellPrint[
      TextCell[
        ""
      , "Program"
      , Evaluatable -> True
      , CellEvaluationFunction -> (evaluationFunction[#]&)
      , CellFrameLabels -> {{None, label}, {None, None}}
      , CellGroupingRules -> "InputGrouping"
      ]
    ]
  ; SelectionMove[EvaluationNotebook[], All, EvaluationCell]
  ; NotebookDelete[]
  ; SelectionMove[EvaluationNotebook[], Next, CellContents]
  )

il est utilisé ainsi:

shellCell[] := evaluatableCell["shell", Import["!"~~#, "Text"] &]

Maintenant, si shellCell[] est évaluée, la cellule d'entrée sera supprimé et remplacé par une nouvelle cellule d'entrée qui donne son contenu comme une commande shell.

Todd Gayley (Wolfram Research) il suffit de m'envoyer un bon hack qui permet d ' "envelopper" les fonctions intégrées avec du code arbitraire. Je pense que je dois partager cet instrument utile. Ce qui suit est la réponse de Todd sur mon question .

Un peu intéressant (?) histoire: ce style de piratage pour "emballer" un la fonction intégrée a été inventée vers 1994 par Robby Villegas et I, ironiquement pour le Message de fonction, dans un paquet appelé ErrorHelp que j'ai écrit pour le journal de Mathematica à l'époque. Il a été utilisé à plusieurs reprises, par beaucoup de gens, depuis. C'est un peu un initié tromper, mais je pense qu'il est juste de dire qu'il est devenu canonique façon d'injecter votre propre code dans la définition d'un haut- fonction. Il fait le travail très bien. Vous pouvez, bien sûr, à mettre l' variable $ inMsg dans n'importe quel contexte privé que vous souhaitez.

Unprotect[Message];

Message[args___] := Block[{$inMsg = True, result},
   "some code here";
   result = Message[args];
   "some code here";
   result] /; ! TrueQ[$inMsg]

Protect[Message];

ce n'est pas une ressource complète, donc je la jette ici dans la section des réponses, mais je l'ai trouvé très utile pour comprendre les questions de vitesse (qui, malheureusement, est une grande partie de ce que la programmation Mathematica est au sujet).

timeAvg[func_] := Module[
{x = 0, y = 0, timeLimit = 0.1, p, q, iterTimes = Power[10, Range[0, 10]]},
Catch[
 If[(x = First[Timing[(y++; Do[func, {#}]);]]) > timeLimit,
    Throw[{x, y}]
    ] & /@ iterTimes
 ] /. {p_, q_} :> p/iterTimes[[q]]
];
Attributes[timeAvg] = {HoldAll};

L'Usage est alors simplement timeAvg@funcYouWantToTest .

EDIT: M. Assistant a fourni une version simplifiée qui fait disparaître les Throw et Catch et est un peu plus facile à analyser:

SetAttributes[timeAvg, HoldFirst]
timeAvg[func_] := Do[If[# > 0.3, Return[#/5^i]] & @@ 
                     Timing @ Do[func, {5^i}]
                     ,{i, 0, 15}]

EDIT: Voici une version de acl (extrait de ici ):

timeIt::usage = "timeIt[expr] gives the time taken to execute expr, \
  repeating as many times as necessary to achieve a total time of 1s";

SetAttributes[timeIt, HoldAll]
timeIt[expr_] := Module[{t = Timing[expr;][[1]], tries = 1},
  While[t < 1., tries *= 2; t = Timing[Do[expr, {tries}];][[1]];]; 
  t/tries]

Internal`InheritedBlock

j'ai appris récemment l'existence d'une telle fonction utile comme Internal`InheritedBlock , de ce message de Daniel Lichtblau dans le groupe de discussion officiel.

comme je comprends, Internal`InheritedBlock permet de passer une copie d'une fonction de sortie à l'intérieur du Block domaine d'application:

In[1]:= Internal`InheritedBlock[{Message},
Print[Attributes[Message]];
Unprotect[Message];
Message[x___]:=Print[{{x},Stack[]}];
Sin[1,1]
]
Sin[1,1]
During evaluation of In[1]:= {HoldFirst,Protected}
During evaluation of In[1]:= {{Sin::argx,Sin,2},{Internal`InheritedBlock,CompoundExpression,Sin,Print,List}}
Out[1]= Sin[1,1]
During evaluation of In[1]:= Sin::argx: Sin called with 2 arguments; 1 argument is expected. >>
Out[2]= Sin[1,1]

je pense que cette fonction peut être très utile pour tous ceux qui ont besoin de modifier intégré fonctions temporairement!

la Comparaison avec le Bloc

définissons une fonction:

a := Print[b]

nous souhaitons maintenant transmettre une copie de cette fonction dans le champ d'application Block . Le procès naïf ne donne pas ce que nous voulons:

In[2]:= Block[{a = a}, OwnValues[a]]

During evaluation of In[9]:= b

Out[2]= {HoldPattern[a] :> Null}

essaie maintenant D'utiliser la définition retardée dans le premier argument de Block (c'est une caractéristique non documentée aussi):

In[3]:= Block[{a := a}, OwnValues[a]]
Block[{a := a}, a]

Out[3]= {HoldPattern[a] :> a}

During evaluation of In[3]:= b

nous voir que dans ce cas a fonctionne, mais nous n'avons pas une copie de l'original a à l'intérieur de la portée Block .

essayons maintenant Internal`InheritedBlock :

In[5]:= Internal`InheritedBlock[{a}, OwnValues[a]]

Out[5]= {HoldPattern[a] :> Print[b]}

nous avons une copie de la définition originale de a à l'intérieur du champ d'application de Block et nous pouvons la modifier comme nous le voulons sans affecter la définition globale de a !

Mathematica est un outil pointu, mais il peut vous couper avec son quelque peu comportement non typé et avalanches de cryptique messages de diagnostic . Une façon de traiter cela est de définir les fonctions en suivant cet idiome:

ClearAll@zot
SetAttributes[zot, ...]
zot[a_] := ...
zot[b_ /; ...] := ...
zot[___] := (Message[zot::invalidArguments]; Abort[])

C'est beaucoup de boilerplate, que je suis souvent tenté de sauter. Surtout quand il s'agit de prototypage, ce qui arrive souvent dans Mathematica. Alors, j'utilise une macro appelé define qui me permet de rester discipliné, avec beaucoup moins passe-partout.

un usage de base de define est comme ceci:

define[
  fact[0] = 1
; fact[n_ /; n > 0] := n * fact[n-1]
]

fact[5]

120

il ne semble pas beaucoup à première vue, mais il ya quelques avantages cachés. Le premier service que define fournit est qu'il applique automatiquement ClearAll au symbole défini. Cela permet de s'assurer qu'il n'y a pas de définitions manquantes -- un phénomène courant au cours de la période initiale. développement d'une fonction.

Le deuxième, c'est que la fonction définie est automatiquement "fermé". Par ceci je veux dire que la fonction émettra un message et annulera s'il est invoqué avec une liste d'arguments qui n'est pas assortie d'une des définitions:

fact[-1]

define::badargs: There is no definition for 'fact' applicable to fact[-1].
$Aborted

il s'agit de la valeur primaire de define , qui saisit une classe d'erreur très courante.

une autre commodité est une façon concise de préciser attributs sur la fonction définie. Faisons la fonction Listable :

define[
  fact[0] = 1
; fact[n_ /; n > 0] := n * fact[n-1]
, Listable
]

fact[{3, 5, 8}]

{6, 120, 40320}

en plus de tous les attributs normaux, define accepte un attribut supplémentaire appelé Open . Cela empêche define d'ajouter la définition d'erreur fourre-tout à la fonction:

define[
  successor[x_ /; x > 0] := x + 1
, Open
]

successor /@ {1, "hi"}

{2, successor["hi"]}

Plusieurs attributs peuvent être définis pour une fonction:

define[
  flatHold[x___] := Hold[x]
, {Flat, HoldAll}
]

flatHold[flatHold[1+1, flatHold[2+3]], 4+5]

Hold[1 + 1, 2 + 3, 4 + 5]

sans plus attendre, voici la définition de define :

ClearAll@define
SetAttributes[define, HoldAll]
define[body_, attribute_Symbol] := define[body, {attribute}]
define[body:(_Set|_SetDelayed), attributes_List:{}] := define[CompoundExpression[body], attributes]
define[body:CompoundExpression[((Set|SetDelayed)[name_Symbol[___], _])..], attributes_List:{}] :=
  ( ClearAll@name
  ; SetAttributes[name, DeleteCases[attributes, Open]]
  ; If[!MemberQ[attributes, Open]
    , def:name[___] := (Message[define::badargs, name, Defer@def]; Abort[])
    ]
  ; body
  ;
  )
def:define[___] := (Message[define::malformed, Defer@def]; Abort[])

define::badargs = "There is no definition for '``' applicable to ``.";
define::malformed = "Malformed definition: ``";

l'implémentation exposée ne supporte ni up-values, ni currying, ni patterns plus généraux que la simple définition de fonction. Elle reste cependant utile.

Démarrer sans un carnet vierge d'ouvrir

j'ai été ennuyé par avoir Mathematica commencer avec un carnet vide ouvert. Je pourrais fermer ce carnet avec un script, mais il resterait ouvert brièvement. Mon hack est de créer un fichier Invisible.nb contenant:

Notebook[{},Visible->False]

et ajoutez ceci à mon Kernel\init.m :

If[Length[Notebooks["Invisible*"]] > 0, 
  NotebookClose[Notebooks["Invisible*"][[1]]]
]

SetOptions[$FrontEnd,
  Options[$FrontEnd, NotebooksMenu] /. 
    HoldPattern["Invisible.nb" -> {__}] :> Sequence[]
]

je commence maintenant Mathematica en ouvrant Invisible.nb

là peut-être une meilleure façon, mais cela m'a bien servi.

---

"sur mesure Fold et FoldList

Fold[f, x] est rendu équivalent à Fold[f, First@x, Rest@x]

incidemment, je crois que cela pourrait trouver son chemin dans une version future de Mathematica.

Surprise! Cette mesure a été mise en œuvre, bien qu'elle le soit actuellement. documentés. J'ai été informé qu'il a été mis en œuvre en 2011 par Oliver Ruebenkoenig, apparemment peu de temps après que j'ai posté ceci. Merci Oliver Ruebenkoenig!

Unprotect[Fold, FoldList]

Fold[f_, h_[a_, b__]] := Fold[f, Unevaluated @ a, h @ b]
FoldList[f_, h_[a_, b__]] := FoldList[f, Unevaluated @ a, h @ b]

(* Faysal's recommendation to modify SyntaxInformation *)
SyntaxInformation[Fold]     = {"ArgumentsPattern" -> {_, _, _.}};
SyntaxInformation[FoldList] = {"ArgumentsPattern" -> {_, _., {__}}};

Protect[Fold, FoldList]

mis à Jour pour permettre cela:

SetAttributes[f, HoldAll]
Fold[f, Hold[1 + 1, 2/2, 3^3]]

f[f[1 + 1, 2/2], 3^3]

---

"Partition Dynamique "

Voir Mathematica.SE post # 7512 for a nouvelle version de cette fonction.

souvent je veux diviser une liste selon une séquence de longueurs.

exemple de pseudo-code:

partition[{1,2,3,4,5,6}, {2,3,1}]

sortie: {{1,2}, {3,4,5}, {6}}

j'ai trouvé ceci:

dynP[l_, p_] := 
 MapThread[l[[# ;; #2]] &, {{0} ~Join~ Most@# + 1, #} &@Accumulate@p]

que j'ai ensuite complété avec ceci, y compris le test d'argument:

dynamicPartition[l_List, p : {_Integer?NonNegative ..}] :=
  dynP[l, p] /; Length@l >= Tr@p

dynamicPartition[l_List, p : {_Integer?NonNegative ..}, All] :=
  dynP[l, p] ~Append~ Drop[l, Tr@p] /; Length@l >= Tr@p

dynamicPartition[l_List, p : {_Integer?NonNegative ..}, n__ | {n__}] :=
  dynP[l, p] ~Join~ Partition[l ~Drop~ Tr@p, n] /; Length@l >= Tr@p

le le troisième argument contrôle ce qui arrive aux éléments au-delà de la spécification split.

---

Szabolc's Mathematica tricks

celui que j'utilise le plus souvent est la palette de données tabulaires en pâte

CreatePalette@
 Column@{Button["TSV", 
    Module[{data, strip}, 
     data = NotebookGet[ClipboardNotebook[]][[1, 1, 1]];
     strip[s_String] := 
      StringReplace[s, RegularExpression["^\s*(.*?)\s*$"] -> ""];
     strip[e_] := e;
     If[Head[data] === String, 
      NotebookWrite[InputNotebook[], 
       ToBoxes@Map[strip, ImportString[data, "TSV"], {2}]]]]], 
   Button["CSV", 
    Module[{data, strip}, 
     data = NotebookGet[ClipboardNotebook[]][[1, 1, 1]];
     strip[s_String] := 
      StringReplace[s, RegularExpression["^\s*(.*?)\s*$"] -> ""];
     strip[e_] := e;
     If[Head[data] === String, 
      NotebookWrite[InputNotebook[], 
       ToBoxes@Map[strip, ImportString[data, "CSV"], {2}]]]]], 
   Button["Table", 
    Module[{data}, data = NotebookGet[ClipboardNotebook[]][[1, 1, 1]];
     If[Head[data] === String, 
      NotebookWrite[InputNotebook[], 
       ToBoxes@ImportString[data, "Table"]]]]]}

---

Modifier les données externes de l'intérieur de Compile

récemment Daniel Lichtblau a montré cette méthode que je n'avais jamais vu avant. À mon avis, il étend considérablement l'utilité de Compile

ll = {2., 3., 4.};
c = Compile[{{x}, {y}}, ll[[1]] = x; y];

c[4.5, 5.6]

ll

(* Out[1] = 5.6  *)

(* Out[2] = {4.5, 3., 4.}  *)

Générale PDF/FEM à l'exportation problèmes et solutions

1) c'est complètement inattendu et non documenté, mais Mathematica exporte et sauve des graphiques dans les formats PDF et EPS en utilisant un ensemble de définitions de style qui diffère de celui utilisé pour l'affichage des blocs-notes sur l'écran. Par défaut, les Notebooks sont affichés à l'écran dans l'environnement de style "Working" (qui est la valeur par défaut pour l'option ScreenStyleEvironment global $FrontEnd ) mais sont imprimé dans le "Printout" style de l'environnement (qui est la valeur par défaut pour le PrintingStyleEnvironment global $FrontEnd en option). Quand on exporte des graphiques dans des formats raster tels que GIF et PNG ou dans le format EMF Mathematica génère des graphiques qui ressemble exactement comme il regarde Bloc-notes. Il semble que l'environnement de style "Working" soit utilisé pour le rendu dans ce cas. Mais ce n'est pas le cas lorsque vous exportez/enregistrez quelque chose dans les formats PDF ou EPS! Dans ce cas, le "Printout" style environnement est utilisé par défaut qui diffère très profondément de l'environnement de" travail " style. Tout d'abord, le "Printout" les ensembles d'environnement de style Magnification à 80% . Deuxièmement, il utilise ses propres valeurs pour les tailles de police de différents styles, ce qui entraîne des changements de taille de police incohérents dans le fichier PDF génaré par rapport à la représentation originale à l'écran. Ce dernier peut être appelé FontSize fluctuations qui sont très ennuyeux. Mais heureusement cela peut être évité en mettant le PrintingStyleEnvironment global $FrontEnd option de "travailler" :

SetOptions[$FrontEnd, PrintingStyleEnvironment -> "Working"]

2 ) le problème commun avec l'exportation au format EMF est que la plupart des programmes (non seulement Mathematica ) générer un fichier qui semble agréable à la taille par défaut, mais devient laid lorsque vous zoomez. C'est parce que metafiles sont échantillonné à la résolution de l'écran fidélité . La qualité du fichier EMF généré peut être améliorée par Magnify ing l'objet graphique original de sorte que l'exactitude de l'échantillonnage des graphiques originaux devient beaucoup plus précise. Comparez deux fichiers:

graphics1 = 
  First@ImportString[
    ExportString[Style["a", FontFamily -> "Times"], "PDF"], "PDF"];
graphics2 = Magnify[graphics1, 10];
Export["C:\test1.emf", graphics1]
Export["C:\test2.emf", graphics2]

si vous insérez ces fichiers dans Microsoft Word et les zoomer, vous verrez que le premier" a "a scié dessus alors que le second n'a pas (testé avec Mathematica 6).

une Autre façon par le biais de ImageResolution a été suggéré par Chris Degnen (cette option n'a d'effet qu'au moins à partir de Mathematica 8):

Export["C:\test1.emf", graphics1]
Export["C:\test2.emf", graphics1, ImageResolution -> 300]

3) dans Mathematica nous avons trois façons de convertir les graphiques en metafile: via Export à "EMF" (méthode fortement recommandée: produit metafile avec la plus haute qualité possible), via Save selection As... menu article ( produit un chiffre beaucoup moins précis , non recommandé) et via Edit ► Copy As ► Metafile article de menu ( je recommande fortement contre cette route ).

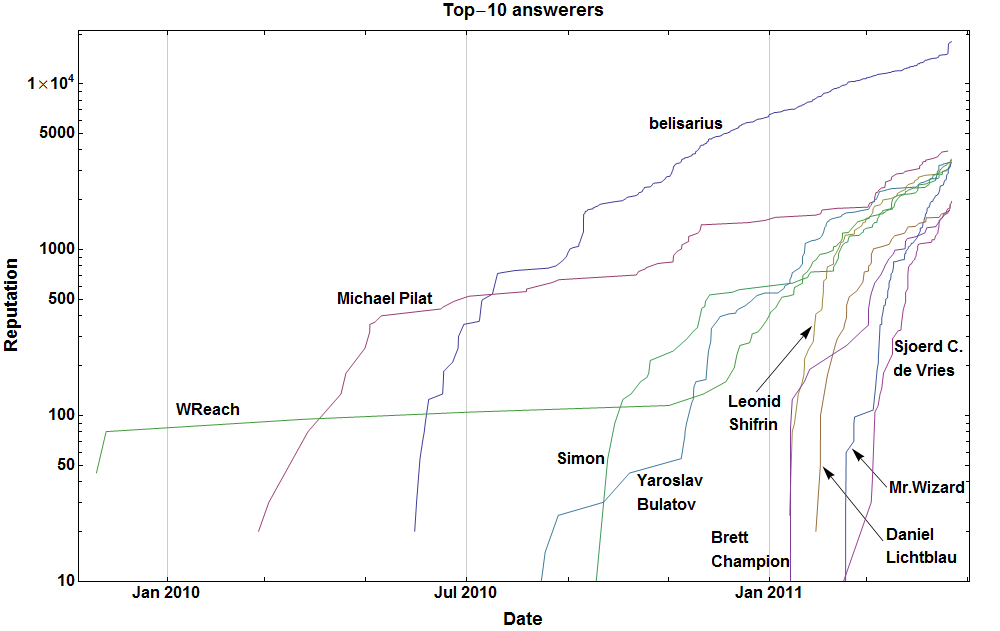
par demande populaire, le code pour générer le Top-10 so answererers parcelle (sauf annotations ) en utilisant le so API .

getRepChanges[userID_Integer] :=
 Module[{totalChanges},
  totalChanges = 
   "total" /. 
    Import["http://api.stackoverflow.com/1.1/users/" <> 
      ToString[userID] <> "/reputation?fromdate=0&pagesize=10&page=1",
      "JSON"];
  Join @@ Table[
    "rep_changes" /. 
     Import["http://api.stackoverflow.com/1.1/users/" <> 
       ToString[userID] <> 
       "/reputation?fromdate=0&pagesize=10&page=" <> ToString[page], 
      "JSON"],
    {page, 1, Ceiling[totalChanges/10]}
    ]
  ]

topAnswerers = ({"display_name", 
      "user_id"} /. #) & /@ ("user" /. ("top_users" /. 
      Import["http://api.stackoverflow.com/1.1/tags/mathematica/top-\
answerers/all-time", "JSON"]))

repChangesTopUsers =
  Monitor[Table[
    repChange = 
     ReleaseHold[(Hold[{DateList[
              "on_date" + AbsoluteTime["January 1, 1970"]], 
             "positive_rep" - "negative_rep"}] /. #) & /@ 
        getRepChanges[userID]] // Sort;
    accRepChange = {repChange[[All, 1]], 
       Accumulate[repChange[[All, 2]]]}\[Transpose],
    {userID, topAnswerers[[All, 2]]}
    ], userID];

pl = DateListLogPlot[
  Tooltip @@@ 
   Take[({repChangesTopUsers, topAnswerers[[All, 1]]}\[Transpose]), 
    10], Joined -> True, Mesh -> None, ImageSize -> 1000, 
  PlotRange -> {All, {10, All}}, 
  BaseStyle -> {FontFamily -> "Arial-Bold", FontSize -> 16}, 
  DateTicksFormat -> {"MonthNameShort", " ", "Year"}, 
  GridLines -> {True, None}, 
  FrameLabel -> (Style[#, FontSize -> 18] & /@ {"Date", "Reputation", 
      "Top-10 answerers", ""})]

"1519130920 la mise en Cache" expressions

je trouve ces fonctions très utiles pour cacher n'importe quelle expression. La chose intéressante ici pour ces deux fonctions est que l'expression retenue elle-même est utilisée comme clé du Cache de hashtable/symbole ou CacheIndex, par rapport à la memoization bien connue dans mathematica où vous ne pouvez résultat de cache que si la fonction est définie comme f[x_] := f[x] = ... De sorte que vous pouvez mettre en cache une partie d'un code, c'est utile si une fonction doit être appelée plusieurs fois mais seulement quelques parties du code ne doivent pas être recalculées.

pour mettre en cache une expression indépendamment de ses arguments.

SetAttributes[Cache, HoldFirst];
c:Cache[expr_] := c = expr;

Ex: Cache[Pause[5]; 6]
Cache[Pause[5]; 6]

la deuxième fois que l'expression retourne 6 sans attendre.

pour mettre en cache une expression utilisant une expression alias qui peut dépendre d'un argument de l'expression mise en cache.

SetAttributes[CacheIndex, HoldRest];
c:CacheIndex[index_,expr_] := c = expr;

Ex: CacheIndex[{"f",2},x=2;y=4;x+y]

si l'expr prend un certain temps à calculer, il est beaucoup plus rapide de évaluer {"f", 2} par exemple pour récupérer le résultat caché.

Pour une variation de ces fonctions afin d'avoir un localisée cache (ie. la mémoire cache est automatiquement libérée en dehors de la construction du bloc) voir ce post éviter les appels répétés à L'Interpolation

suppression des valeurs en cache

pour supprimer les valeurs mises en cache lorsque vous ne connaissez pas le nombre de définitions d'une fonction. Je considère que les définitions ont un blanc quelque part dans leurs arguments.

DeleteCachedValues[f_] := 
       DownValues[f] = Select[DownValues[f], !FreeQ[Hold@#,Pattern]&];

pour supprimer les valeurs mises en cache lorsque vous connaissez le nombre de définitions d'une fonction (va légèrement plus vite).

DeleteCachedValues[f_,nrules_] := 
       DownValues[f] = Extract[DownValues[f], List /@ Range[-nrules, -1]];

cela utilise le fait que les définitions d'une fonction sont à la fin de leur liste de valeurs inférieures, les valeurs mises en cache sont avant.

utilisation de symboles pour stocker des données et des fonctions apparentées à un objet

voici aussi fonctions intéressantes à utiliser des symboles comme des objets.

il est déjà bien connu que vous pouvez stocker des données dans des symboles et y accéder rapidement en utilisant des valeurs inférieures

mysymbol["property"]=2;

vous pouvez accéder à la liste des clés (ou propriétés) d'un symbole en utilisant ces fonctions basées sur ce que dreeves soumis dans un post sur ce site:

SetAttributes[RemoveHead, {HoldAll}];
RemoveHead[h_[args___]] := {args};
NKeys[symbol_] := RemoveHead @@@ DownValues[symbol(*,Sort->False*)][[All,1]];
Keys[symbol_] := NKeys[symbol] /. {x_} :> x;

j'utilise souvent cette fonction pour afficher toutes les informations contenues dans les valeurs basses d'un symbole:

PrintSymbol[symbol_] :=
  Module[{symbolKeys},
    symbolKeys = Keys[symbol];
    TableForm@Transpose[{symbolKeys, symbol /@ symbolKeys}]
  ];

enfin voici une façon simple de créer un symbole qui se comporte comme un objet dans la programmation orientée objet (il reproduit juste le comportement le plus basique de OOP mais je trouve la syntaxe élégante):

Options[NewObject]={y->2};
NewObject[OptionsPattern[]]:=
  Module[{newObject},
    newObject["y"]=OptionValue[y];

    function[newObject,x_] ^:= newObject["y"]+x;
    newObject /: newObject.function2[x_] := 2 newObject["y"]+x;

    newObject
  ];

Les propriétés

sont stockées en tant que valeurs et méthodes en tant que valeurs ascendantes retardées dans le symbole créé par le Module qui est retourné. J'ai trouvé la syntaxe pour function2 qui est la syntaxe oo habituelle pour les fonctions dans Tree la structure des données dans Mathematica .

pour une liste des types existants de valeurs de chaque symbole, voir http://reference.wolfram.com/mathematica/tutorial/PatternsAndTransformationRules.html et http://www.verbeia.com/mathematica/tips/HTMLLinks/Tricks_Misc_4.html .

essayez par exemple

x = NewObject[y -> 3];
function[x, 4]
x.function2[5]

Vous pouvez aller plus loin si vous souhaitez émuler objet héritage à l'aide d'un paquet appelé Héritrules disponible ici http://library.wolfram.com/infocenter/MathSource/671 /

vous pouvez aussi stocker la définition de la fonction non pas dans newObject mais dans un symbole de type, donc si NewObject renvoie le type [newObject] au lieu de newObject vous pouvez définir la fonction et function2 comme ceci en dehors de NewObject (et pas à l'intérieur) et avoir le même usage qu'avant.

function[type[object_], x_] ^:= object["y"] + x;
type /: type[object_].function2[x_] := 2 object["y"]+x;

Use UpValues[type] pour voir que la fonction et la function2 sont définies dans le symbole de type.

D'autres idées sur cette dernière syntaxe sont présentées ici https://mathematica.stackexchange.com/a/999/66 .

version améliorée de SelectEquivalents

@rcollyer: Merci beaucoup d'avoir ramené quelques équivalents à la surface, c'est une fonction incroyable. Voici une version améliorée de SelectEquivalents énumérés ci-dessus avec plus de possibilités et d'options, il est plus facile à utiliser.

Options[SelectEquivalents] = 
   {
      TagElement->Identity,
      TransformElement->Identity,
      TransformResults->(#2&) (*#1=tag,#2 list of elements corresponding to tag*),
      MapLevel->1,
      TagPattern->_,
      FinalFunction->Identity
   };

SelectEquivalents[x_List,OptionsPattern[]] := 
   With[
      {
         tagElement=OptionValue@TagElement,
         transformElement=OptionValue@TransformElement,
         transformResults=OptionValue@TransformResults,
         mapLevel=OptionValue@MapLevel,
         tagPattern=OptionValue@TagPattern,
         finalFunction=OptionValue@FinalFunction
      }
      ,
      finalFunction[
         Reap[
            Map[
               Sow[
                  transformElement@#
                  ,
                  {tagElement@#}
               ]&
               , 
               x
               , 
               {mapLevel}
            ] 
            , 
            tagPattern
            , 
            transformResults
         ][[2]]
      ]
   ];

Voici des exemples d'utilisation de cette version:

à l'Aide de Mathematica Rassembler/Collecter correctement

comment feriez-vous une fonction pivotable dans Mathematica?

Mathematica rapide 2D binning algorithme

Interne'Bag

Daniel Lichtblau décrit ici une structure de données internes intéressante pour les listes croissantes.

mise en œuvre D'un Quadtree en Mathematica

fonctions de débogage

ces deux messages pointent vers des fonctions utiles pour le débogage:

comment déboguer lors de l'écriture de petits ou grands codes en utilisant Mathematica? workbench? débogueur mma? ou quelque chose d'autre? (ShowIt)

https://stackoverflow.com/questions/5459735/the-clearest-way-to-represent-mathematicas-evaluation-sequence/5527117#5527117 (TraceView)

Voici une autre fonction basée sur Reap et Sow pour extraire des expressions de différentes parties d'un programme et les stocker dans un symbole.

SetAttributes[ReapTags,HoldFirst];
ReapTags[expr_]:=
   Module[{elements},
      Reap[expr,_,(elements[#1]=#2/.{x_}:>x)&];
      elements
   ];

voici un exemple

ftest[]:=((*some code*)Sow[1,"x"];(*some code*)Sow[2,"x"];(*some code*)Sow[3,"y"]);
s=ReapTags[ftest[]];
Keys[s]
s["x"]
PrintSymbol[s] (*Keys and PrintSymbol are defined above*)

autres ressources

Voici une liste de liens intéressants pour apprendre but:

, Une collection de Mathematica ressources d'apprentissage

mis à jour ici: https://mathematica.stackexchange.com/a/259/66

mes fonctions Utilitaires (je les ai intégrées à MASH, ce qui est mentionné dans la question):

pr = WriteString["stdout", ##]&;            (* More                           *)
prn = pr[##, "\n"]&;                        (*  convenient                    *)
perr = WriteString["stderr", ##]&;          (*   print                        *)
perrn = perr[##, "\n"]&;                    (*    statements.                 *)
re = RegularExpression;                     (* I wish mathematica             *)
eval = ToExpression[cat[##]]&;              (*  weren't so damn               *)
EOF = EndOfFile;                            (*   verbose!                     *)
read[] := InputString[""];                  (* Grab a line from stdin.        *)
doList[f_, test_] :=                        (* Accumulate list of what f[]    *)
  Most@NestWhileList[f[]&, f[], test];      (*  returns while test is true.   *)
readList[] := doList[read, #=!=EOF&];       (* Slurp list'o'lines from stdin. *)
cat = StringJoin@@(ToString/@{##})&;        (* Like sprintf/strout in C/C++.  *)
system = Run@cat@##&;                       (* System call.                   *)
backtick = Import[cat["!", ##], "Text"]&;   (* System call; returns stdout.   *)
slurp = Import[#, "Text"]&;                 (* Fetch contents of file as str. *)
                                            (* ABOVE: mma-scripting related.  *)
keys[f_, i_:1] :=                           (* BELOW: general utilities.      *)
  DownValues[f, Sort->False][[All,1,1,i]];  (* Keys of a hash/dictionary.     *)
SetAttributes[each, HoldAll];               (* each[pattern, list, body]      *)
each[pat_, lst_, bod_] := ReleaseHold[      (*  converts pattern to body for  *)
  Hold[Cases[Evaluate@lst, pat:>bod];]];    (*   each element of list.        *)
some[f_, l_List] := True ===                (* Whether f applied to some      *)
  Scan[If[f[#], Return[True]]&, l];         (*  element of list is True.      *)
every[f_, l_List] := Null ===               (* Similarly, And @@ f/@l         *)
  Scan[If[!f[#], Return[False]]&, l];       (*  (but with lazy evaluation).   *)

un truc que j'ai utilisé, qui vous permet d'émuler la façon dont la plupart des fonctions intégrées fonctionnent avec de mauvais arguments (en envoyant un message et en retournant ensuite le formulaire entier non évalué) exploite une bizarrerie de la façon Condition fonctionne lorsqu'il est utilisé dans une définition. Si foo ne devrait fonctionner qu'avec un seul argument:

foo[x_] := x + 1;
expr : foo[___] /; (Message[foo::argx, foo, Length@Unevaluated[expr], 1]; 
                    False) := Null; (* never reached *)

si vous avez des besoins plus complexes, il est facile de prendre en compte la validation de l'argument et la génération du message comme un fonction indépendante. Vous pouvez faire des choses plus élaborées en utilisant des effets secondaires dans Condition au-delà de générer des messages, mais à mon avis la plupart d'entre eux tombent dans la catégorie "sleazy hack" et devrait être évitée si possible.

aussi, dans la catégorie" métaprogrammation", si vous avez un paquet Mathematica ( .m ), vous pouvez utiliser le "HeldExpressions" élément pour obtenir toutes les expressions dans le fichier enveloppé dans HoldComplete . Cela rend il est beaucoup plus facile de retracer les choses que d'utiliser des recherches textuelles. Malheureusement, il n'y a pas de moyen facile de faire la même chose avec un ordinateur portable, mais vous pouvez obtenir toutes les expressions d'entrée en utilisant quelque chose comme ce qui suit:

inputExpressionsFromNotebookFile[nb_String] :=
 Cases[Get[nb],
  Cell[BoxData[boxes_], "Input", ___] :>
   MakeExpression[StripBoxes[boxes], StandardForm],
  Infinity]

enfin, vous pouvez utiliser le fait que Module émule des fermetures lexicales pour créer l'équivalent des types de référence. Voici une simple pile (qui utilise comme bonus une variation du Condition ):

ClearAll[MakeStack, StackInstance, EmptyQ, Pop, Push, Peek]
 With[{emptyStack = Unique["empty"]},
  Attributes[StackInstance] = HoldFirst;
  MakeStack[] :=
   Module[{backing = emptyStack},
    StackInstance[backing]];

  StackInstance::empty = "stack is empty";

  EmptyQ[StackInstance[backing_]] := (backing === emptyStack);

  HoldPattern[
    Pop[instance : StackInstance[backing_]]] /;
    ! EmptyQ[instance] || (Message[StackInstance::empty]; False) :=
   (backing = Last@backing; instance);

  HoldPattern[Push[instance : StackInstance[backing_], new_]] :=
   (backing = {new, backing}; instance);

  HoldPattern[Peek[instance : StackInstance[backing_]]] /;
    ! EmptyQ[instance] || (Message[StackInstance::empty]; False) :=
   First@backing]

Maintenant, vous pouvez imprimer les éléments d'une liste dans l'ordre inverse dans un inutilement alambiqué!

With[{stack = MakeStack[], list},
 Do[Push[stack, elt], {elt, list}];

 While[!EmptyQ[stack],
  Print[Peek@stack];
  Pop@stack]]

symboles du système D'impression définitions sans contexte préprogrammé

la fonction contextFreeDefinition[] ci-dessous tentera d'Imprimer la définition d'un symbole sans le contexte le plus courant. La définition peut alors être copiée sur Workbench et formatée pour la lisibilité (la Sélectionner, clic droit, Source - > Format)

Clear[commonestContexts, contextFreeDefinition]

commonestContexts[sym_Symbol, n_: 1] := Quiet[
  Commonest[
   Cases[Level[DownValues[sym], {-1}, HoldComplete], 
    s_Symbol /; FreeQ[$ContextPath, Context[s]] :> Context[s]], n],
  Commonest::dstlms]

contextFreeDefinition::contexts = "Not showing the following contexts: `1`";

contextFreeDefinition[sym_Symbol, contexts_List] := 
 (If[contexts =!= {}, Message[contextFreeDefinition::contexts, contexts]];
  Internal`InheritedBlock[{sym}, ClearAttributes[sym, ReadProtected];
   Block[{$ContextPath = Join[$ContextPath, contexts]}, 
    Print@InputForm[FullDefinition[sym]]]])

contextFreeDefinition[sym_Symbol, context_String] := 
 contextFreeDefinition[sym, {context}]

contextFreeDefinition[sym_Symbol] := 
 contextFreeDefinition[sym, commonestContexts[sym]]

---

withRules []

mise en garde: Cette fonction ne localise pas les variables de la même façon que With et Module font, ce qui signifie que les constructions de localisation imbriquées ne fonctionneront pas comme prévu. withRules[{a -> 1, b -> 2}, With[{a=3}, b_ :> b]] va remplacer a et b dans les emboîtés With et Rule , tandis que With ne fait pas cela.

c'est une variante de With qui utilise des règles au lieu de = et := :

ClearAll[withRules]
SetAttributes[withRules, HoldAll]
withRules[rules_, expr_] :=
  Internal`InheritedBlock[
    {Rule, RuleDelayed},
    SetAttributes[{Rule, RuleDelayed}, HoldFirst];
    Unevaluated[expr] /. rules
  ]

j'ai trouvé cela utile en nettoyant le code écrit pendant l'expérimentation et en localisant des variables. Parfois je me retrouve avec des listes de paramètres sous la forme de {par1 -> 1.1, par2 -> 2.2} . Avec withRules les valeurs de paramètre sont faciles à injecter dans le code précédemment écrit en utilisant des variables globales.

"1519250920 d'Utilisation" est comme With :

withRules[
  {a -> 1, b -> 2},
  a+b
]

---

Anticrénelage graphiques 3D

C'est un technique très simple pour les graphiques 3D antialias même si votre matériel graphique ne le supporte pas nativement.

antialias[g_, n_: 3] := 
  ImageResize[Rasterize[g, "Image", ImageResolution -> n 72], Scaled[1/n]]

voici un exemple:

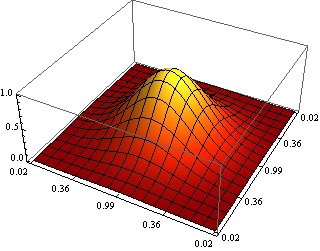
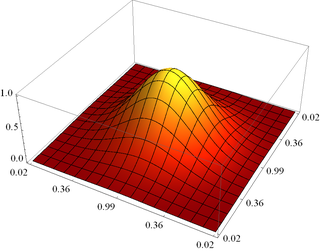
notez qu'une grande valeur pour n ou une grande taille d'image a tendance à exposer les bugs du pilote graphique ou à introduire des artefacts.

---

" Notebook diff functionality

La fonctionnalité

est disponible dans le paquet <<AuthorTools` et (au moins dans la version 8) dans le contexte non documenté NotebookTools` . Ceci est un petit GUI pour distinguer deux carnets qui sont actuellement ouverts:

PaletteNotebook@DynamicModule[
  {nb1, nb2}, 
  Dynamic@Column[
    {PopupMenu[Dynamic[nb1], 
      Thread[Notebooks[] -> NotebookTools`NotebookName /@ Notebooks[]]], 
     PopupMenu[Dynamic[nb2], 
      Thread[Notebooks[] -> NotebookTools`NotebookName /@ Notebooks[]]], 
     Button["Show differences", 
      CreateDocument@NotebookTools`NotebookDiff[nb1, nb2]]}]
  ]

fonctions pures récursives ( #0 ) semblent être l'un des coins les plus sombres de la langue. Voici quelques exemples non-triviaux de leur utilisation, où cela est vraiment utile (non pas qu'ils ne peuvent pas être faits sans elle). Ce qui suit est une fonction assez concise et raisonnablement rapide pour trouver des composants connectés dans un graphique, donné une liste des bords spécifiés comme paires de Sommets:

ClearAll[setNew, componentsBFLS];
setNew[x_, x_] := Null;
setNew[lhs_, rhs_]:=lhs:=Function[Null, (#1 := #0[##]); #2, HoldFirst][lhs, rhs];

componentsBFLS[lst_List] := Module[{f}, setNew @@@ Map[f, lst, {2}];
   GatherBy[Tally[Flatten@lst][[All, 1]], f]];

ce qui se passe ici est que nous cartographions d'abord un symbole chacun des nombres de vertex, et puis mettre en place une façon que, compte tenu d'une paire de Sommets {f[5],f[10]} , dire, puis f[5] évaluerait à f[10] . La fonction pure récursive est utilisée comme compresseur de chemin (pour configurer la mémoization de telle sorte qu'au lieu de longues chaînes comme f[1]=f[3],f[3]=f[4],f[4]=f[2], ... , les valeurs mémoizées soient corrigées chaque fois qu'une nouvelle "racine" du composant est découverte. Cela donne une vitesse importante. Parce que nous utilisons la mission, nous en avons besoin pour être HoldAll, ce qui rend cette construction même les plus obscures et les plus attractives ). Cette fonction est le résultat d'une discussion de groupe de mathématiques en ligne et hors ligne impliquant Fred Simons, Szabolcs Horvat,DrMajorBob et votre serviteur. Exemple:

In[13]:= largeTest=RandomInteger[{1,80000},{40000,2}];

In[14]:= componentsBFLS[largeTest]//Short//Timing
Out[14]= {0.828,{{33686,62711,64315,11760,35384,45604,10212,52552,63986,  
     <<8>>,40962,7294,63002,38018,46533,26503,43515,73143,5932},<<10522>>}}

il est certainement beaucoup plus lent qu'un intégré, mais pour la taille du code, assez rapide encore IMO.

autre exemple: voici une réalisation récursive de Select , basée sur des listes liées et des fonctions pures récursives:

selLLNaive[x_List, test_] :=
  Flatten[If[TrueQ[test[#1]],
     {#1, If[#2 === {}, {}, #0 @@ #2]},
     If[#2 === {}, {}, #0 @@ #2]] & @@ Fold[{#2, #1} &, {}, Reverse[x]]];

par exemple,

In[5]:= Block[
         {$RecursionLimit= Infinity},
         selLLNaive[Range[3000],EvenQ]]//Short//Timing

Out[5]= {0.047,{2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,
 <<1470>>,2972,2974,2976,2978,2980,2982,2984,2986,2988,2990,
  2992,2994,2996,2998,3000}}

il n'est cependant pas correctement récursif de queue, et va souffler la pile (planter le noyau) pour des listes plus grandes. Voici la version recursive:

selLLTailRec[x_List, test_] :=
Flatten[
 If[Last[#1] === {},
  If[TrueQ[test[First[#1]]],
   {#2, First[#1]}, #2],
  (* else *)
  #0[Last[#1],
   If[TrueQ[test[First[#1]]], {#2, First[#1]}, #2]
   ]] &[Fold[{#2, #1} &, {}, Reverse[x]], {}]];

par exemple,

In[6]:= Block[{$IterationLimit= Infinity},
       selLLTailRec[Range[500000],EvenQ]]//Short//Timing
Out[6]= {2.39,{2,4,6,8,10,12,14,16,18,20,22,
       <<249978>>,499980,499982,499984,499986,499988,499990,499992,
        499994,499996,499998,500000}} 

c'est une recette du livre de Stan Wagon...utilisez-le lorsque la parcelle intégrée se comporte de façon erratique en raison d'un manque de précision

Options[PrecisePlot] = {PrecisionGoal -> 6};
PrecisePlot[f_, {x_, a_, b_}, opts___] := Module[{g, pg},
   pg = PrecisionGoal /. {opts} /. Options[PrecisePlot];
   SetAttributes[g, NumericFunction];
   g[z_?InexactNumberQ] := Evaluate[f /. x -> z];
   Plot[N[g[SetPrecision[y, \[Infinity]]], pg], {y, a, b},
    Evaluate[Sequence @@ FilterRules[{opts}, Options[Plot]]]]];

j'utilise souvent l'astuce suivante de Kristjan Kannike quand j'ai besoin de "dictionary-like" behavior from Mathematica's downvalues

index[downvalue_, 
   dict_] := (downvalue[[1]] /. HoldPattern[dict[x_]] -> x) // 
   ReleaseHold;
value[downvalue_] := downvalue[[-1]];
indices[dict_] := 
  Map[#[[1]] /. {HoldPattern[dict[x_]] -> x} &, DownValues[dict]] // 
   ReleaseHold;
values[dict_] := Map[#[[-1]] &, DownValues[dict]];
items[dict_] := Map[{index[#, dict], value[#]} &, DownValues[dict]];
indexQ[dict_, index_] := 
  If[MatchQ[dict[index], HoldPattern[dict[index]]], False, True];

(* Usage example: *)
(* Count number of times each subexpression occurs in an expression *)
expr = Cos[x + Cos[Cos[x] + Sin[x]]] + Cos[Cos[x] + Sin[x]]
Map[(counts[#] = If[indexQ[counts, #], counts[#] + 1, 1]; #) &, expr, Infinity];
items[counts]

lorsque les résultats de l'évaluation sont confus, il est parfois utile de transférer les étapes de l'évaluation dans un fichier texte

SetAttributes[recordSteps, HoldAll];
recordSteps[expr_] :=
 Block[{$Output = List@OpenWrite["~/temp/msgStream.m"]}, 
  TracePrint[Unevaluated[expr], _?(FreeQ[#, Off] &), 
   TraceInternal -> True];
  Close /@ $Output;
  Thread[Union@
    Cases[ReadList["~/temp/msgStream.m", HoldComplete[Expression]], 
     symb_Symbol /; 
       AtomQ@Unevaluated@symb && 
        Context@Unevaluated@symb === "System`" :> 
      HoldComplete@symb, {0, Infinity}, Heads -> True], HoldComplete]
  ]

(* Usage example: *)
(* puts steps of evaluation of 1+2+Sin[5]) into ~/temp/msgStream.m *)
recordSteps[1+2+Sin[5]]

il est possible D'exécuter MathKernel en mode discontinu en utilisant options en ligne de commande -batchinput et -batchoutput :

math -batchinput -batchoutput < input.m > outputfile.txt

(où input.m est le fichier d'entrée par lots se terminant par le caractère newline, outputfile.txt est le fichier vers lequel la sortie sera redirigée).

Dans Mathematica v.>=6, le MathKernel a sans papiers option de ligne de commande:

-noicon

qui contrôle si le MathKernel aura l'icône visible sur la barre des tâches (au moins sous Windows).

le FrontEnd (au moins de v. 5) a l'option de ligne de commande non documentée

-b

qui désactive l'écran de projection et permet d'exécuter le Mathematica FrontEnd beaucoup plus rapide

et option

-directlaunch

qui désactive le mécanisme qui lance le plus récent Mathematica version installée au lieu de lancer la version associée .fichiers nb dans le registre du système.

une autre façon de faire probablement est :

au lieu de lancer le Mathematica.exe binaire dans le répertoire d'installation, lancez le Mathematica.exe binaires SystemFiles\FrontEnd\Binaires\Windows. Le premier est un simple lanceur programme qui tente son plus dur pour demandes de redirection pour l'ouverture notes pour les exemplaires courants de la interface utilisateur. Le dernier est le interface utilisateur binaire lui-même.

il est pratique de combiner la dernière option de ligne de commande avec la définition de L'option frontale globale VersionedPreferences->True qui désactive le partage des préférences entre différents Mathematica versions installées :

SetOptions[$FrontEnd, VersionedPreferences -> True]

(ce qui précède doit être évalué dans la version la plus récente de Mathematica installée.)

dans Mathematica 8 ceci est contrôlé dans la boîte de dialogue Préférences, dans le volet système, sous le paramètre" Créer et maintenir des préférences frontales spécifiques à la version " .

il est possible de obtenez la liste incomplète des options en ligne de commande de L'interface en utilisant la clé non documentée -h (le code pour Windows):

SetDirectory[$InstallationDirectory <> 
   "\SystemFiles\FrontEnd\Binaries\Windows\"];
Import["!Mathematica -h", "Text"]

donne:

Usage:  Mathematica [options] [files]
Valid options:
    -h (--help):  prints help message
    -cleanStart (--cleanStart):  removes existing preferences upon startup
    -clean (--clean):  removes existing preferences upon startup
    -nogui (--nogui):  starts in a mode which is initially hidden
    -server (--server):  starts in a mode which disables user interaction
    -activate (--activate):  makes application frontmost upon startup
    -topDirectory (--topDirectory):  specifies the directory to search for resources and initialization files
    -preferencesDirectory (--preferencesDirectory):  specifies the directory to search for user AddOns and preference files
    -password (--password):  specifies the password contents
    -pwfile (--pwfile):  specifies the path for the password file
    -pwpath (--pwpath):  specifies the directory to search for the password file
    -b (--b):  launches without the splash screen
    -min (--min):  launches as minimized

autres options:

-directLaunch:  force this FE to start
-32:  force the 32-bit FE to start
-matchingkernel:  sets the frontend to use the kernel of matching bitness
-Embedding:  specifies that this instance is being used to host content out of process

---

Existe-t-il d'autres options en ligne de commande potentiellement utiles du MathKernel et du FrontEnd? Merci de partager si vous le savez.

question connexe .

mes hacks préférés sont de petites macros générant du code qui vous permettent de remplacer un tas de commandes standard boilerplate par une courte. Vous pouvez aussi créer des commandes pour ouvrir/créer des notebooks.

voici ce que j'utilise depuis un certain temps dans Mon flux quotidien Mathematica.

1. Faire un ordinateur portable ont un contexte privé, de charger le package(s) j'ai besoin, rendre la la sauvegarde automatique.
2. après avoir travaillé avec ce carnet pendant un certain temps, je voudrais faire quelques calculs à jeter dans un carnet séparé, avec son propre contexte privé, tout en ayant accès aux définitions que j'ai utilisé dans le" principal " carnet. Parce que j'ai mis en place le contexte privé, cela nécessite d'ajuster manuellement $ContextPath

faire tout cela à la main est une douleur, alors automatisons! Tout d'abord, un certain code d'utilité:

(* Credit goes to Sasha for SelfDestruct[] *)
SetAttributes[SelfDestruct, HoldAllComplete];
SelfDestruct[e_] := (If[$FrontEnd =!= $Failed,
   SelectionMove[EvaluationNotebook[], All, EvaluationCell]; 
   NotebookDelete[]]; e)

writeAndEval[nb_,boxExpr_]:=(
    NotebookWrite[nb,  CellGroupData[{Cell[BoxData[boxExpr],"Input"]}]];
    SelectionMove[nb, Previous, Cell]; 
    SelectionMove[nb, Next, Cell];
    SelectionEvaluate[nb];
)

ExposeContexts::badargs = 
  "Exposed contexts should be given as a list of strings.";
ExposeContexts[list___] := 
 Module[{ctList}, ctList = Flatten@List@list; 
  If[! MemberQ[ctList, Except[_String]],AppendTo[$ContextPath, #] & /@ ctList, 
   Message[ExposeContexts::badargs]];
  $ContextPath = DeleteDuplicates[$ContextPath];
  $ContextPath]

    Autosave[x:(True|False)] := SetOptions[EvaluationNotebook[],NotebookAutoSave->x];

maintenant, créons une macro qui va mettre les cellules suivantes dans le carnet:

SetOptions[EvaluationNotebook[], CellContext -> Notebook]
Needs["LVAutils`"]
Autosave[True]

et voici le macro:

MyPrivatize[exposedCtxts : ({__String} | Null) : Null]:=
  SelfDestruct@Module[{contBox,lvaBox,expCtxtBox,assembledStatements,strList},
    contBox = MakeBoxes[SetOptions[EvaluationNotebook[], CellContext -> Notebook]];
    lvaBox = MakeBoxes[Needs["LVAutils`"]];

    assembledStatements = {lvaBox,MakeBoxes[Autosave[True]],"(*********)"};
    assembledStatements = Riffle[assembledStatements,"\[IndentingNewLine]"]//RowBox;
    writeAndEval[InputNotebook[],contBox];
    writeAndEval[InputNotebook[],assembledStatements];
    If[exposedCtxts =!= Null,
       strList = Riffle[("\"" <> # <> "\"") & /@ exposedCtxts, ","];
       expCtxtBox = RowBox[{"ExposeContexts", "[", RowBox[{"{", RowBox[strList], "}"}], "]"}];
       writeAndEval[InputNotebook[],expCtxtBox];
      ]
 ]

maintenant quand je tape MyPrivatize[] est crée le contexte privé et charge mon paquet standard. Maintenant, créons une commande qui ouvrira un nouveau bloc-notes scratch avec son propre contexte privé (de sorte que vous pouvez y pirater avec wild abandon sans le risque de foirer le définitions), mais a accès à vos contextes actuels.

SpawnScratch[] := SelfDestruct@Module[{nb,boxExpr,strList},
    strList = Riffle[("\"" <> # <> "\"") & /@ $ContextPath, ","];
    boxExpr = RowBox[{"MyPrivatize", "[",
        RowBox[{"{", RowBox[strList], "}"}], "]"}];
    nb = CreateDocument[];
    writeAndEval[nb,boxExpr];
]

la chose cool à ce sujet est qu'en raison de SelfDestruct , lorsque la commande s'exécute, il ne laisse aucune trace dans le carnet de notes actuel-ce qui est bon, parce que sinon il ne ferait que créer du désordre.

pour les points de style supplémentaires, vous pouvez créer des déclencheurs de mots clés pour ces macros en utilisant InputAutoReplacements , mais je vais laisser ceci comme un exercice pour le lecteur.

PutAppend avec PageWidth -> l'Infini

dans Mathematica l'utilisation de la commande PutAppend est le moyen le plus simple de maintenir un fichier journal courant avec les résultats de calculs intermédiaires. Mais il utilise par défaut le paramètre PageWith->78 lors de l'exportation d'expressions vers un fichier et il n'y a donc aucune garantie que chaque sortie intermédiaire ne prendra qu'une ligne dans le journal.

PutAppend avoir n'importe quelles options elle-même mais en traçant ses évaluations révèle qu'elle est basée sur la fonction OpenAppend qui a l'option PageWith et permet de changer sa valeur par défaut par la commande SetOptions :

In[2]:= Trace[x>>>"log.txt",TraceInternal->True]
Out[2]= {x>>>log.txt,{OpenAppend[log.txt,CharacterEncoding->PrintableASCII],OutputStream[log.txt,15]},Null}

de sorte que nous pouvons obtenir PutAppend d'ajouter une seule ligne à la fois en définissant:

SetOptions[OpenAppend, PageWidth -> Infinity]

---

mise à jour

il y a un bug introduit dans la version 10 (corrigé dans la version 11.3): SetOptions n'affecte plus le comportement de OpenWrite et OpenAppend .

une solution est de mettre en œuvre votre propre version de PutAppend avec explicite PageWidth -> Infinity option:

Clear[myPutAppend]
myPutAppend[expr_, pathtofile_String] :=
 (Write[#, expr]; Close[#];) &[OpenAppend[pathtofile, PageWidth -> Infinity]]

notez que nous pouvons également le mettre en œuvre via WriteString comme indiqué dans cette réponse , mais dans ce cas, il sera nécessaire de convertir expression dans le InputForm correspondant via ToString[expr, InputForm] .

j'étais juste en train de regarder à travers un de mes paquets pour l'inclure dans ceci, et j'ai trouvé quelques messages que j'ai définis qui font des merveilles: Debug::<some name> . Par défaut, ils sont désactivés, donc ne produisent pas beaucoup de frais généraux. Mais, je peux polluer mon code avec eux, et les allumer si j'ai besoin de comprendre exactement comment un peu de code se comporte.

une des choses qui me dérange au sujet des constructions intégrées de détermination de la portée est qu'elles évaluent toutes les définitions des variables locales à la fois, de sorte que vous ne pouvez pas écrire par exemple

With[{a = 5, b = 2 * a},
    ...
]

donc il y a un moment j'ai inventé une macro appelée WithNest qui vous permet de faire ceci. Je le trouve pratique, car il vous permet de garder les fixations variables locales sans avoir à faire quelque chose comme

Module[{a = 5,b},
    b = 2 * a;
    ...
]

à la fin, la meilleure façon que j'ai pu trouver à faire c'était en utilisant un symbole spécial pour le rendre plus facile de revenir sur la liste des reliures, et j'ai mis la définition dans son propre paquet pour garder ce symbole caché. Peut-être que quelqu'un a une solution plus simple à ce problème?

si vous voulez l'essayer, mettez ce qui suit dans un fichier appelé Scoping.m :

BeginPackage["Scoping`"];

WithNest::usage=
"WithNest[{var1=val1,var2=val2,...},body] works just like With, except that
values are evaluated in order and later values have access to earlier ones.
For example, val2 can use var1 in its definition.";

Begin["`Private`"];

(* Set up a custom symbol that works just like Hold. *)
SetAttributes[WithNestHold,HoldAll];

(* The user-facing call.  Give a list of bindings and a body that's not
our custom symbol, and we start a recursive call by using the custom
symbol. *)
WithNest[bindings_List,body:Except[_WithNestHold]]:=
WithNest[bindings,WithNestHold[body]];

(* Base case of recursive definition *)
WithNest[{},WithNestHold[body_]]:=body;

WithNest[{bindings___,a_},WithNestHold[body_]]:=
WithNest[
{bindings},
WithNestHold[With[List@a,body]]];

SyntaxInformation[WithNest]={"ArgumentsPattern"->{{__},_}};
SetAttributes[WithNest,{HoldAll,Protected}];

End[];

EndPackage[];

ce code crée une palette qui télécharge la sélection pour Stack Exchange comme une image. Sur Windows, un bouton supplémentaire est fourni qui donne un rendu plus fidèle de la sélection.

Copiez le code dans une cellule de bloc-notes et évaluez. Puis sortir la palette de la sortie, et l'installer en utilisant Palettes -> Install Palette...

Si vous avez des problèmes avec elle, postez un commentaire ici. Télécharger la version portable ici .

---

Begin["SOUploader`"];

Global`palette = PaletteNotebook@DynamicModule[{},

   Column[{
     Button["Upload to SE",
      With[{img = rasterizeSelection1[]},
       If[img === $Failed, Beep[], uploadWithPreview[img]]],
      Appearance -> "Palette"],

     If[$OperatingSystem === "Windows",

      Button["Upload to SE (pp)",
       With[{img = rasterizeSelection2[]},
        If[img === $Failed, Beep[], uploadWithPreview[img]]],
       Appearance -> "Palette"],

      Unevaluated@Sequence[]
      ]
     }],

   (* Init start *)
   Initialization :>
    (

     stackImage::httperr = "Server returned respose code: `1`";
     stackImage::err = "Server returner error: `1`";

     stackImage[g_] :=
      Module[
       {getVal, url, client, method, data, partSource, part, entity,
        code, response, error, result},

       getVal[res_, key_String] :=
        With[{k = "var " <> key <> " = "},
         StringTrim[

          First@StringCases[
            First@Select[res, StringMatchQ[#, k ~~ ___] &],
            k ~~ v___ ~~ ";" :> v],
          "'"]
         ];

       data = ExportString[g, "PNG"];

       JLink`JavaBlock[
        url = "http://stackoverflow.com/upload/image";
        client =
         JLink`JavaNew["org.apache.commons.httpclient.HttpClient"];
        method =
         JLink`JavaNew[
          "org.apache.commons.httpclient.methods.PostMethod", url];
        partSource =
         JLink`JavaNew[
          "org.apache.commons.httpclient.methods.multipart.\
ByteArrayPartSource", "mmagraphics.png",
          JLink`MakeJavaObject[data]@toCharArray[]];
        part =
         JLink`JavaNew[
          "org.apache.commons.httpclient.methods.multipart.FilePart",
          "name", partSource];
        part@setContentType["image/png"];
        entity =
         JLink`JavaNew[
          "org.apache.commons.httpclient.methods.multipart.\
MultipartRequestEntity", {part}, method@getParams[]];
        method@setRequestEntity[entity];
        code = client@executeMethod[method];
        response = method@getResponseBodyAsString[];
        ];

       If[code =!= 200, Message[stackImage::httperr, code];
        Return[$Failed]];
       response = StringTrim /@ StringSplit[response, "\n"];

       error = getVal[response, "error"];
       result = getVal[response, "result"];
       If[StringMatchQ[result, "http*"],
        result,
        Message[stackImage::err, error]; $Failed]
       ];

     stackMarkdown[g_] :=
      "![Mathematica graphics](" <> stackImage[g] <> ")";

     stackCopyMarkdown[g_] := Module[{nb, markdown},
       markdown = Check[stackMarkdown[g], $Failed];
       If[markdown =!= $Failed,
        nb = NotebookCreate[Visible -> False];
        NotebookWrite[nb, Cell[markdown, "Text"]];
        SelectionMove[nb, All, Notebook];
        FrontEndTokenExecute[nb, "Copy"];
        NotebookClose[nb];
        ]
       ];

     (* Returns available vertical screen space,
     taking into account screen elements like the taskbar and menu *)


     screenHeight[] := -Subtract @@
        Part[ScreenRectangle /. Options[$FrontEnd, ScreenRectangle],
         2];

     uploadWithPreview[img_Image] :=
      CreateDialog[
       Column[{
         Style["Upload image to the Stack Exchange network?", Bold],
         Pane[

          Image[img, Magnification -> 1], {Automatic,
           Min[screenHeight[] - 140, 1 + ImageDimensions[img][[2]]]},
          Scrollbars -> Automatic, AppearanceElements -> {},
          ImageMargins -> 0
          ],
         Item[
          ChoiceButtons[{"Upload and copy MarkDown"}, \
{stackCopyMarkdown[img]; DialogReturn[]}], Alignment -> Right]
         }],
       WindowTitle -> "Upload image to Stack Exchange?"
       ];

     (* Multiplatform, fixed-width version.
        The default max width is 650 to fit Stack Exchange *)
     rasterizeSelection1[maxWidth_: 650] :=
      Module[{target, selection, image},
       selection = NotebookRead[SelectedNotebook[]];
       If[MemberQ[Hold[{}, $Failed, NotebookRead[$Failed]], selection],

        $Failed, (* There was nothing selected *)

        target =
         CreateDocument[{}, WindowSelected -> False, Visible -> False,
           WindowSize -> maxWidth];
        NotebookWrite[target, selection];
        image = Rasterize[target, "Image"];
        NotebookClose[target];
        image
        ]
       ];

     (* Windows-only pixel perfect version *)
     rasterizeSelection2[] :=
      If[
       MemberQ[Hold[{}, $Failed, NotebookRead[$Failed]],
        NotebookRead[SelectedNotebook[]]],

       $Failed, (* There was nothing selected *)

       Module[{tag},
        FrontEndExecute[
         FrontEndToken[FrontEnd`SelectedNotebook[], "CopySpecial",
          "MGF"]];
        Catch[
         NotebookGet@ClipboardNotebook[] /.
          r_RasterBox :>
           Block[{},
            Throw[Image[First[r], "Byte", ColorSpace -> "RGB"], tag] /;
              True];
         $Failed,
         tag
         ]
        ]
       ];
     )
   (* Init end *)
   ]

End[];

je suis sûr que beaucoup de gens ont rencontré la situation où ils courent quelques trucs, réalisant que non seulement coincé le programme, mais ils ont aussi n'ont pas sauvé pour les 10 dernières minutes!

EDIT

après avoir souffert de cela pendant un certain temps, j'ai un jour découvert que on peut créer auto-save de l'intérieur du Mathematica code. Je pense que l'utilisation d'un tel auto-save ont m'a beaucoup aidé dans le passé, et j'ai toujours pensé que la possibilité elle-même était quelque chose que pas beaucoup de gens sont conscients qu'ils peuvent faire.

le code original que j'ai utilisé est en bas. Grâce aux commentaires, j'ai découvert que c'est problématique, et qu'il est beaucoup mieux de le faire d'une manière alternative, en utilisant ScheduledTask (qui ne fonctionnera que dans Mathematica 8).

Le Code

peut être trouvée dans cette réponse de Sjoerd C. de Vries (Comme je ne suis pas sûr que ce soit correct de le Copier ici, je le laisse comme un lien seulement.)

---

la solution ci-dessous utilise Dynamic . Il sauvera le carnet toutes les 60 secondes, mais apparemment seulement si sa cellule est visible . Je ne le laisse ici que pour des raisons d'achèvement. (et pour les utilisateurs de Mathematica 6 et 7)

/ EDIT

pour le résoudre j'utilise ce code au début d'un carnet:

Dynamic[Refresh[NotebookSave[]; DateString[], UpdateInterval -> 60]]

cela économisera votre travail toutes les 60 secondes.

Je la préfère à NotebookAutoSave[] parce qu'il sauve avant que l'entrée est traitée, et parce que certains fichiers sont plus de texte que d'entrée.

Je l'ai trouvé ici à l'origine: http://en.wikipedia.org/wiki/Talk:Mathematica#Criticisms

notez qu'une fois cette ligne exécutée, l'enregistrement aura lieu même si vous fermez et rouvrez votre fichier (tant que la mise à jour dynamique est activée).

aussi, puisqu'il n'y a pas d'annulation dans Mathematica , faites attention de ne pas supprimer tout votre contenu, car l'économie le rendra irréversible (par précaution je supprime ce code de chaque bloc-notes fini)

celui-ci a été écrit par Alberto Di Lullo, (qui ne semble pas être sur le débordement de la pile).

CopyToClipboard , pour Mathematica 7 (en Mathematica 8 il est construit en)

CopyToClipboard[expr_] := 
  Module[{nb}, 
   nb = CreateDocument[Null, Visible -> False, WindowSelected -> True];
   NotebookWrite[nb, Cell[OutputFormData@expr], All];
   FrontEndExecute[FrontEndToken[nb, "Copy"]];
   NotebookClose@nb];

Original post: http://forums.wolfram.com/mathgroup/archive/2010/Jun/msg00148.html

j'ai trouvé cette routine utile pour copier de grands nombres réels au bloc-notes sous forme décimale ordinaire. Par exemple: CopyToClipboard["123456789.12345"]

Cell[OutputFormData@expr] supprime soigneusement les guillemets.

rappelez-vous que le Livre de Mathematica est également disponible en ligne à http://reference.wolfram.com/legacy/v5_2 / - bien qu'il soit remplacé par la documentation actuelle à http://reference.wolfram.com

je trouve qu'il est vraiment utile lors du développement de paquets pour ajouter ce raccourci clavier à mon fichier SystemFiles/FrontEnd/TextResources/Windows/KeyEventTranslations.tr .

(* Evaluate Initialization Cells: Real useful for reloading library changes. *)

Item[KeyEvent["i", Modifiers -> {Control, Command}],
    FrontEndExecute[
        FrontEndToken[
            SelectedNotebook[],
            "EvaluateInitialization"]]],

ensuite pour chaque Packagename.m je fais un PackagenameTest.nb bloc-notes pour le test et les 2 premières cellules du bloc-notes sont définies comme des cellules d'initialisation. Dans la première cellule j'ai mis

Needs["PackageManipulations`"]

pour charger la bibliothèque très utile PackageManipulations qui a été écrit par Leonid. Le la deuxième cellule contient

PackageRemove["Packagename`Private`"]
PackageRemove["Packagename`"]
PackageReload["Packagename`"]

qui font tous le rechargement du paquet. Notez que les deux premières lignes ne sont là que pour Remove tous les symboles que j'aime garder les contextes aussi propres que possible.

alors le flux de travail pour écrire et tester un paquet devient quelque chose comme ça.

1. Enregistrer les modifications Packagename.m .
2. passer à PackagenameTest.nb et faire CTRL + ALT + i .

cela provoque les cellules d'initialisation à recharger le paquet, ce qui rend l'essai très simple.

fonction suivante format[expr_] peut être utilisé pour indenter/formater des expressions non formattées mathematica qui s'étendent au-dessus d'une page

indent[str_String, ob_String, cb_String, delim_String] := 
  Module[{ind, indent, f, tab}, ind = 0; tab = "    ";
   indent[i_, tab_, nl_] := nl <> Nest[tab <> ToString[#] &, "", i];
   f[c_] := (indent[ind, "", " "] <> c <> indent[++ind, tab, "\n"]) /;StringMatchQ[ob, ___ ~~ c ~~ ___];
   f[c_] := (indent[--ind, "", " "] <> c <> indent[ind, tab, "\n"]) /;StringMatchQ[cb, ___ ~~ c ~~ ___];
   f[c_] := (c <> indent[ind, tab, "\n"]) /;StringMatchQ[delim, ___ ~~ c ~~ ___];
   f[c_] := c;
   f /@ Characters@str // StringJoin];
format[expr_] := indent[expr // InputForm // ToString, "[({", "])}", ";"];

(*    
format[Hold@Module[{ind, indent, f, tab}, ind = 0; tab = "    ";
 indent[i_, tab_, nl_] := nl <> Nest[tab <> ToString[#] &, "", i];
 f[c_] := (indent[ind, "", " "] <> c <> indent[++ind, tab, "\n"]) /;StringMatchQ[ob, ___ ~~ c ~~ ___];
 f[c_] := (indent[--ind, "", " "] <> c <> indent[ind, tab, "\n"]) /;StringMatchQ[cb, ___ ~~ c ~~ ___];
 f[c_] := (c <> indent[ind, tab, "\n"]) /;StringMatchQ[delim, ___ ~~ c ~~ ___];
 f[c_] := c;
 f /@ Characters@str // StringJoin]]
*)

---

ref: https://codegolf.stackexchange.com/questions/3088/indent-a-string-using-given-parentheses