Qu'est-ce que la notation Big Cho représente exactement?

commençons par comprendre ce que sont big O, big Theta et big Omega. Ils sont tous ensembles de fonctions.

Big O est de donner supérieur asymptotique lié , tandis que les grandes Omega est de donner une limite inférieure. Big Theta donne les deux.

Tout ce qui est Ө(f(n)) est aussi O(f(n)) , mais pas l'inverse.

T(n) est dit être dans Ө(f(n)) si elle est tous les deux en O(f(n)) et en Omega(f(n)) .

Dans des ensembles de terminologie, Ө(f(n)) est le intersection de O(f(n)) et Omega(f(n))

par exemple , merge sort le pire des cas est à la fois O(n*log(n)) et Omega(n*log(n)) - et est donc aussi Ө(n*log(n)) , mais il est aussi O(n^2) , depuis n^2 est asymptotiquement" plus grand " qu'elle. Cependant, il est pas Ө(n^2) , puisque l'algorithme n'est pas Omega(n^2) .

une explication mathématique un peu plus profonde

O(n) est une limite supérieure asymptotique. Si T(n) est O(f(n)) , cela signifie que d'un certain n0 , il y a une constante C tel que T(n) <= C * f(n) . D'un autre côté, big-Omega dit qu'il y a une constante C2 telle que T(n) >= C2 * f(n)) ).

ne pas confondre!

à ne pas confondre avec l'analyse du pire, du meilleur et de la moyenne des cas: tous les trois (Omega, O, Theta) notation sont et non liés à l'analyse du meilleur, du pire et de la moyenne des cas d'algorithmes. Chacun d'eux peut être appliqué à chaque analyse.

nous l'utilisons habituellement pour analyser la complexité des algorithmes (comme le sort de fusion exemple ci-dessus). Lorsque nous disons "algorithme A est O(f(n)) ", ce que nous voulons vraiment dire est "le des algorithmes de complexité dans le pire des ^{1 "1519800920 l'analyse du cas" est O(f(n)) " - sens - échelles "similaire" (ou formellement, pas pire que) la fonction f(n) .}

pourquoi nous soucions de la liaison asymptotique d'un algorithme?

bien, il y a plusieurs raisons à cela, mais je crois que les plus importantes d'entre elles sont:

1. il est beaucoup plus difficile de déterminer le exact fonction de complexité, ainsi nous "compromettons" sur les grandes-o/grandes-thêta notations, qui sont suffisamment informatives en théorie.
2. le nombre exact d'ops est aussi dépendant de la plate-forme . Par exemple, si nous avons un vecteur (liste) de 16 chiffres. Combien d'opérations ça va prendre? La réponse est: ça dépend. Certains CPU permettent des ajouts vectoriels, tandis que d'autres ne le font pas, de sorte que la réponse varie entre différentes implémentations et différentes machines, ce qui est un indésirable propriété. La notation big-O est cependant beaucoup plus constante entre les machines et les implémentations.

Pour illustrer cette question, regardez les graphiques suivants:

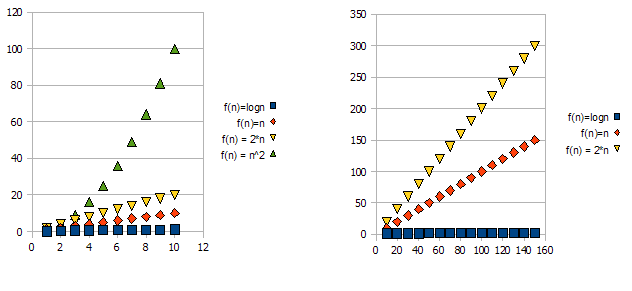
Il est clair que f(n) = 2*n est "pire" que f(n) = n . Mais la différence n'est pas aussi radicale que c'est de l'autre fonction. Nous pouvons voir que f(n)=logn rapidement arriver beaucoup plus faible que les autres fonctions, et f(n) = n^2 devient rapidement beaucoup plus haut que les autres.

ainsi-pour les raisons ci-dessus, nous "ignorons" les facteurs constants (2* dans l'exemple des graphiques), et ne prenons que la notation big-O.

dans l'exemple ci - dessus, f(n)=n, f(n)=2*n sera à la fois dans O(n) et dans Omega(n) - et donc sera également dans Theta(n) .

d'autre part - f(n)=logn sera en O(n) (c'est "mieux" que f(n)=n ), mais ne sera pas dans Omega(n) - et ne sera donc pas non plus dans Theta(n) .

symétriquement, f(n)=n^2 sera dans Omega(n) , mais pas dans O(n) , et donc - N'est pas non plus Theta(n) .

---

¹ D'habitude, mais pas toujours. quand la classe d'analyse (la pire, moyenne et la meilleure) est manquante, nous voulons vraiment dire le pire cas.

pour répondre à votre question, la notation asymptotique et les fonctions dans la notation asymptotique doivent également être expliquées. Si vous avez la patience de tout lire, les choses seront très claires à la fin.

1. Notation asymptotique

pour penser aux algorithmes, vous pouvez utiliser 2 idées principales:

1. Déterminer combien de temps l'algorithme prend en termes de sa contribution.
2. se concentrer sur la vitesse à laquelle une fonction se développe avec le taille d'entrée; aka taux de croissance de la durée de fonctionnement. Exemple: supposons qu'un algorithme, exécuté sur une entrée de taille n, prenne 6n^2 + 100n + 300 Instructions machine. Le terme 6n ^ 2 devient plus grand que les Termes restants, 100 N + 300, Une fois que n devient assez grand, 20 dans ce cas.

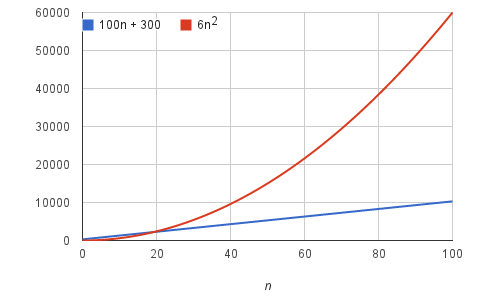
nous dirions que le temps de fonctionnement de cet algorithme augmente comme n^2, en baissant le coefficient 6 et les Termes restants 100 + 300. Peu importe les coefficients que nous utilisons; aussi longtemps que la durée de fonctionnement est a n^2 + b n + C, pour certains nombres a > 0, b, et c, il y aura toujours une valeur de n pour laquelle a n^2 est plus grand que b n + C, et cette différence augmente avec n augmente. En abandonnant les coefficients constants et les Termes moins significatifs, nous utilisons la notation asymptotique.

2. Big-Theta

voici un simple mise en œuvre de la recherche linéaire

var doLinearSearch = function(array) {
  for (var guess = 0; guess < array.length; guess++) {
    if (array[guess] === targetValue) { 
        return guess;  // found it!
    }
  }
  return -1;  // didn't find it
};

• chacun de ces petits calculs prend un temps constant chaque fois qu'il exécute. Si la boucle de for itère n fois, alors le temps pour toutes les itérations de n est c1 * n, où c1 est la somme des temps pour les calculs dans une itération de boucle. Ce code a un peu de surimpression supplémentaire, pour configurer la boucle for (y compris initialiser guess à 0) et éventuellement retourner -1 à la fin. Appelons le temps pour cette c2 aérienne, qui est aussi une constante. Par conséquent, le temps total pour la recherche linéaire dans le pire des cas est c1*n+c2.
• le facteur constant c1 et le terme de bas ordre c2 ne nous renseignent pas sur le taux de croissance de la durée. Ce qui est significatif, c'est que la durée de la recherche linéaire dans le pire des cas croît comme la taille du tableau N. La notation que nous utilisons pour cette durée Est Θ(n). C'est la lettre grecque thêta," et nous dire "grand-Thêta de n" ou juste "thêta de n".

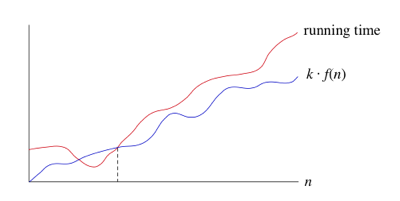
• quand nous disons Qu'un temps de course particulier Est Θ(n), nous disons que lorsque n devient assez grand, le temps de course est au moins k1*n et au plus k2*n Pour certaines constantes k1 et k2. Voici comment penser à Θ(n)

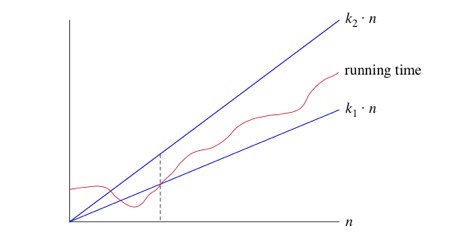
• pour les petites valeurs de n, Nous ne nous soucions pas de savoir comment le temps de fonctionnement se compare avec k1*n ou k2*N. Mais une fois n Grand assez-sur ou à droite de la ligne pointillée-la durée doit être comprise entre k1*n et k2*N. Aussi longtemps que ces constantes k1 et k2 existent, nous disons que le temps de fonctionnement est Θ(n).

• quand nous utilisons la notation big-Θ, Nous disons que nous avons un asymptotiquement limite serrée sur le temps de course. "Asymptotiquement" parce qu'il importe pour seulement de grandes valeurs de N. "Tight bound" parce que nous avons cloué le temps d'exécution à l'intérieur d'un facteur constant au-dessus et au-dessous.

3. Les fonctions de notation asymptotique

• supposons qu'un algorithme prenne un temps constant, quelle que soit la taille de l'entrée. Par exemple, si vous avez reçu un tableau qui est déjà trié en ordre croissant et que vous deviez trouver l'élément minimum, cela prendrait du temps constant, puisque l'élément minimum doit être à l'index 0. Comme nous aimons utiliser un fonction de n dans la notation asymptotique, on peut dire que cet algorithme s'exécute dans le temps Θ(N^0). Pourquoi? Parce que N^0 = 1, et le temps d'exécution de l'algorithme est d'un facteur constant de 1. En pratique, nous n'écrivons pas Θ (N^0), cependant; nous écrivons Θ (1)
• Voici une liste de fonctions dans la notation asymptotique que nous rencontrons souvent lors de l'analyse des algorithmes, de la plus lente à la plus rapide croissance. Cette liste n'est pas exhaustive, il existe de nombreux algorithmes dont le temps d'exécution ne sont pas
• Θ (1) (alias constant search)
• Θ (lg n) (alias binaire)
• Θ (n) (alias recherche linéaire)
• Θ (N*lg n)
• Θ (N^2)
• Θ (N^2*lg n)
• Θ (N^3)

• Θ (2^n)

• noter qu'une fonction exponentielle a^n, où a > 1, croît plus rapidement que n'importe quelle autre fonction. fonction polynomiale n^b, où b est n'importe quelle constante.

4. Notation Big-O

• nous utilisons la notation big-Θ pour lier asymptotiquement la croissance d'un temps de course à l'intérieur de facteurs constants au-dessus et au-dessous. Parfois, nous voulons seulement nous lier d'en haut. Il serait pratique d'avoir une forme de notation asymptotique qui signifie "le temps d'exécution augmente à plus beaucoup, mais il peut se développer plus lentement."Nous utilisons la notation "big-O" pour de telles occasions.
• si un temps de course est O(f(n)), alors pour un temps de course assez grand n, Le temps de course est au maximum k*F (n) pour un certain K constant. Voici comment penser à un temps de course qui est O(F(n)):
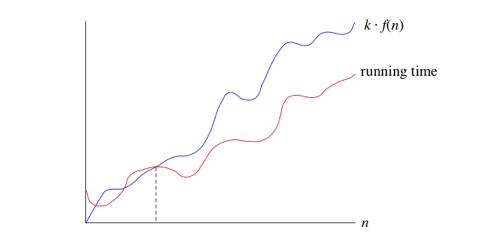
• si vous retournez à la définition de la notation big-Θ, Vous remarquerez qu'elle ressemble beaucoup à la notation big-O, sauf que la notation big-Θ limite la course à partir d'en haut et en bas, plutôt que juste à partir de ci-dessus. Si on dit Qu'une durée Est Θ(f(n)) dans une situation particulière, alors C'est aussi O(F(n)). Par exemple, nous pouvons dire que parce que le pire des cas de temps d'exécution de la recherche binaire Est Θ(lg n), c'est aussi O(LG n). L'inverse n'est pas nécessairement vrai: comme nous l'avons vu, nous pouvons dire que la recherche binaire s'exécute toujours en temps O(lg n) mais pas Qu'elle s'exécute toujours en temps Θ(lg n).
• supposons que vous ayez 10 dollars en poche. Vous allez jusqu'à votre ami et dire, "j'ai un montant de de l'argent dans ma poche, et je te garantis que ce n'est pas plus d'un million de dollars."Votre déclaration est absolument vraie, mais pas terriblement précise. Un million de dollars est une limite supérieure sur 10 dollars, tout comme O(n) est une limite supérieure sur la durée de la recherche binaire.
• autres, imprécises, les limites supérieures de la recherche binaire seraient O(N^2), O(n^3), et O (2^n). Mais aucun de Θ (n),Θ(N^2), Θ(N^3), etθ(2^n) ne serait correct pour décrire le temps de fonctionnement de la recherche binaire dans n'importe quel cas.

5. Notation Big-Ω (Big-Omega)

• Parfois, nous voulons dire qu'un algorithme qui prend au moins une certaine quantité de temps, sans limite supérieure. Nous utilisons la notation big-Ω; c'est la lettre grecque "omega."
• si un temps d'exécution Est Ω (f(n)), Alors pour n assez grand, le temps d'exécution est au moins k*F (n) pour une constante de K. Voici comment penser à un temps d'exécution qui est Ω(f(n)):
• nous disons que le temps de fonctionnement est" big-Ω de f(n)."Nous utilisons la notation big-Ω pour les limites inférieures asymptotiques, car elle limite la croissance du temps de fonctionnement à partir d'en bas pour des tailles d'entrée assez grandes.
• Comme Θ (f(n)) implique automatiquement O(f(n)), il implique aussi automatiquement Ω(f (n)). Nous pouvons donc dire que le temps de traitement le plus mauvais de la recherche binaire Est Ω(lg n). Nous pouvons également faire corriger, mais imprécis, les déclarations utilisant la notation big-Ω. Par exemple, tout comme si vous avez vraiment un million de dollars dans votre poche, vous pouvez sincèrement dire "j'ai une quantité d'argent dans ma poche, et c'est au moins 10 dollars," vous pouvez également dire que le pire des cas de durée de fonctionnement de la recherche binaire Est Ω(1), parce qu'il prend au moins temps constant.

référence: https://www.khanacademy.org

Theta(n): une fonction f(n) appartient à Theta(g(n)) , s'il existe des constantes positives c1 et c2 telles que f(n) peut être pris en sandwich entre c1(g(n)) et c2(g(n)) . I. e il y a une limite supérieure et une limite inférieure.

Thêta(g(n)) = { f(n) : il existe des constantes positives c1,c2 et n1 tel que 0<=c1(g(n))<=f(n)<=c2(g(n)) pour tous les n > = n1}

quand on dit f(n)=c2(g(n)) ou f(n)=c1(g(n)) ça représente une limite asymptotiquement serrée.

O(n): Il ne donne que la limite supérieure (peut ou peut ne pas être serré)

O(g (n)) = { f (n) : Il existe des constantes positives c et n1 telles que 0< = f (n)<=cg (n) POUR TOUS n>=n1}

ex : la limite 2*(n^2) = O(n^2) est asymptotiquement serrée, tandis que la limite 2*n = O(n^2) n'est pas asymptotiquement serrée.

o(n): Il ne donne que la limite supérieure (jamais serré lié)

la différence notable entre O (n) et o (n) EST f (n) est inférieure à cg(n) pour tous n>=n1 mais pas égal à O (n).

ex : 2*n = o(n^2) , mais 2*(n^2) != o(n^2)