Que signifie, pour deux arbres binaires à être isomorphe?
Que signifie pour deux arbres binaires à être isomorphe? J'ai été à la recherche en ligne et je n'arrive pas à trouver une explication claire.
autant que je sache, deux arbres sont isomorphiques s'ils ont la même forme. Donc je devine deux arbres identiques qui peuvent contenir des valeurs différentes dans les noeuds.
3 réponses
isomorphe vient du Grec " même forme "(comme isobar est des points avec la même pression d'air et le polygone signifie" plusieurs côtés") donc votre compréhension est correcte. Mais ne faites pas l'erreur d'assumer la forme dans ce cas est un physique forme (comme l'arbre a une racine, un noeud gauche et un noeud droit; voir ci-dessous par exemple). Les mathématiciens ont leur propre langue que seulement parfois ours le passage d'une relation à l'anglais :-)
Ce n'est pas juste des arbres binaires. En mathématiques, deux structures sont isomorphiques si leurs propriétés sont préservées quelle que soit leur expression (vous pouvez avoir une fonction qui traduit A en B et une autre de B en A sans perte d'information).
Pour votre cas particulier, c'est l'information dans l'arbre qui est conservé. Par exemple, si cette information est les éléments triés {1,2,3} pour que l'arbre ne doit pas être le même physique forme à tous les deux serait être isomorphe:
2 1
/ \ \
1 3 2
\
3
triés lié liste (ou un tableau trié, d'ailleurs) est aussi isomorphe à ceux puisque, dans ce cas, aucune information serait perdue dans les transformations entre les deux.
Si l'arbre binaire a été utilisé d'une manière où l'ordre de tri n'était pas pertinent (c'est à dire, un "sac" sorte de conteneur), l'information serait tout simplement le contenu dans n'importe quel ordre, et toutes les suivantes serait isomorphe (qui seconde le dernier est juste un sac, le dernier est une liste):
2 1 2 3 +---+ +---+ +---+
/ \ \ / \ +-------+ | 3 |->| 1 |->| 2 |
1 3 2 1 2 | 1,3,2 | +---+ +---+ +---+
\ / \ +-------+
3 3 1
bien sûr, un arbre non trié peut être considéré comme un petit gâchis selon vos besoins, mais ce n'est pas pertinent pour cette discussion particulière.
les conditions suivantes doivent être remplies pour que deux arbres soient isomorphiques:
1. Deux Arbres sont isomorphe a ' si et seulement s'ils conservent même pas de niveaux et même pas de sommets dans chaque niveau .
2.Deux arbres sont isomorphiques si et seulement s'ils ont le même spectre de degré .
3.Deux arbres sont isomorphiques si et seulement s'ils ont le même degré de spectre à chaque niveau.
- nombre Total de feuilles descendantes d'un sommet et le nombre de niveaux les sommets sont invariants isomorphiques des arbres.
en termes simples:
Deux arbres sont isomorphiques si un arbre peut être obtenu d'un autre en effectuant un nombre quelconque de flips I. e échange des enfants de gauche et des enfants de droite d'un certain nombre de noeuds .
exemple d'arbres isomorphes:
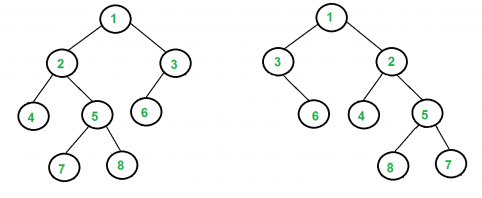
Ref: 1.http://www14.in.tum.de/konferenzen/Jass03/presentations/eterevsky.pdf 2.http://www.geeksforgeeks.org/tree-isomorphism-problem/
je pense que votre compréhension est assez correcte. Si vous ignorez les valeurs et regardez juste la structure, alors pour chaque noeud dans le premier arbre il doit y avoir un noeud correspondant dans l'autre arbre et vice versa.
naturellement, les deux arbres auraient le même nombre de noeuds. En outre, vous pouvez écrire un algorithme (Super-naïf) pour confirmer cet isomorphisme en essayant toutes les fonctions de cartographie possibles, et en s'assurant que pour chaque noeud dans le premier arbre qui obtient cartographié à un noeud dans l'autre, la correspondance correspondante se produit avec le parent et avec les deux enfants. Il y a évidemment des algorithmes efficaces pour le vérifier.
Vous pouvez bénéficier de la lecture sur isomorphisme des graphes tout d'abord, les arbres sont un cas spécial (et plus facile à résoudre) puisqu'ils n'ont pas de cycles.