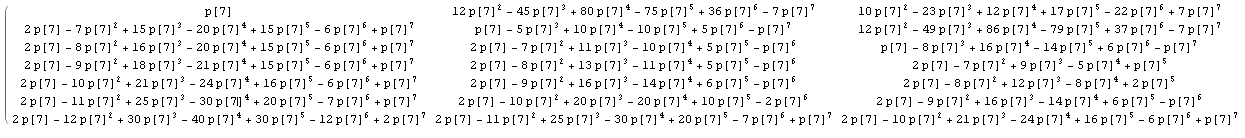Quelle est la distribution que vous obtenez de ce mélange aléatoire cassé?

le célèbre algorithme de Fisher-Yates shuffle peut être utilisé pour permuter au hasard un tableau A de longueur N: 

For k = 1 to N
    Pick a random integer j from k to N
    Swap A[k] and A[j]

une erreur courante qu'on m'a dit encore et encore de ne pas faire est celle-ci: 

For k = 1 to N
    Pick a random integer j from 1 to N
    Swap A[k] and A[j]

C'est-à-dire, au lieu de choisir un entier aléatoire de k À N, vous choisissez un entier aléatoire de 1 à N.

que se passe-t-il si vous faites cette erreur? Je sais que la permutation n'est pas uniformément distribué, mais je ne sais pas quelles garanties il y a sur ce que la distribution sera. En particulier, est-ce que quelqu'un a une expression pour les distributions de probabilité sur les positions finales des éléments?

71
demandé sur GEOCHET 2011-02-27 06:51:05

10 réponses

Une Approche Empirique.

mettons en œuvre L'algorithme erroné dans Mathematica: 

p = 10; (* Range *)
s = {}
For[l = 1, l <= 30000, l++, (*Iterations*)
   a = Range[p];
   For[k = 1, k <= p, k++, 
     i = RandomInteger[{1, p}];
     temp = a[[k]];
     a[[k]] = a[[i]];
     a[[i]] = temp
   ];
   AppendTo[s, a];
]

Maintenant obtenir le nombre de fois que chaque entier est dans chaque position: 

r = SortBy[#, #[[1]] &] & /@ Tally /@ Transpose[s]

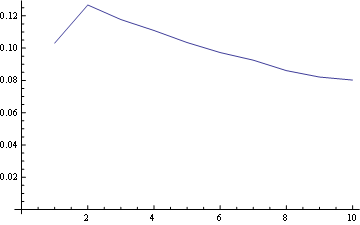
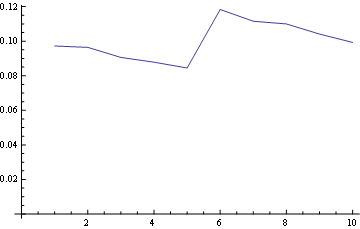
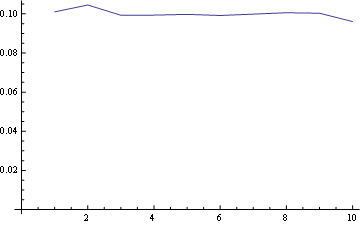
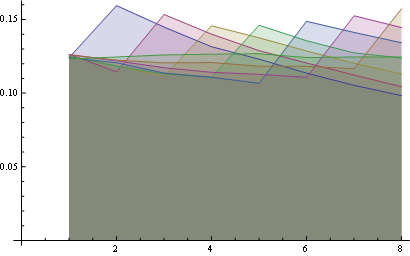
prenons trois positions dans les tableaux résultants et traçons la distribution de fréquence pour chaque entier dans cette position:

pour la position 1 la distribution freq est:

enter image description here

pour la position 5 (Milieu)

enter image description here

et pour la position 10 (dernière):

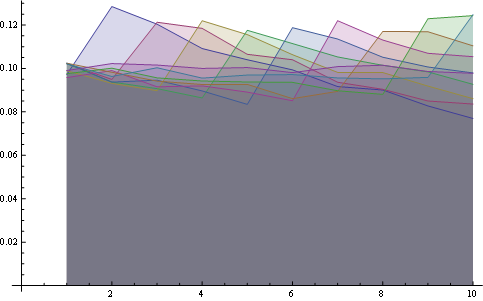
enter image description here

et ici vous avez la distribution pour toutes les positions tracées ensemble:

enter image description here

ici, vous avez de meilleures statistiques sur 8 postes:

enter image description here

quelques observations:

  • pour toutes les positions la probabilité de "1" est le même (1/n).
  • la matrice de probabilité est symétrique en ce qui concerne le grand anti-diagonal
  • ainsi, la probabilité pour n'importe quel nombre dans le dernier la position est également uniforme (1/n)

vous pouvez visualiser ces propriétés en regardant le début de toutes les lignes à partir du même point (première propriété) et la dernière ligne horizontale (troisième propriété).

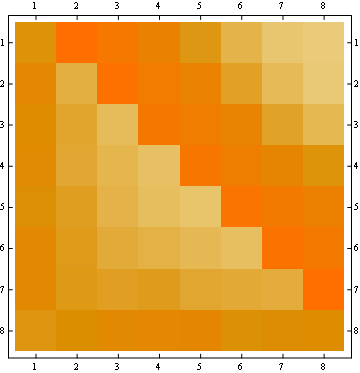
la deuxième propriété peut être vue à partir de l'exemple de représentation matricielle suivant, où les lignes sont les positions, les colonnes sont le nombre d'occupants, et la couleur représente la probabilité expérimentale:

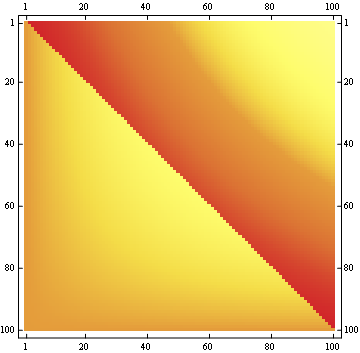
enter image description here

pour une matrice 100x100:

enter image description here

Modifier

juste pour le plaisir, j'ai calculé la formule exacte pour le deuxième élément diagonal (le premier est 1/n). Le reste peut être fait, mais c'est beaucoup de travail. 

h[n_] := (n-1)/n^2 + (n-1)^(n-2) n^(-n)

valeurs vérifiées de n=3 à 6 ( {8/27, 57/256, 564/3125, 7105/46656} )

Modifier

en calculant un peu le calcul général explicite dans @wnoise answer, nous pouvons obtenir un peu plus d'informations.

remplaçant 1 / n Par p[n], de sorte que les calculs ne sont pas évalués, nous obtenons par exemple pour la première partie de la matrice avec n=7 (cliquer pour un agrandissement)):

enter image description here

qui, après comparaison avec les résultats pour d'autres valeurs de n, permet d'identifier quelques séquences entières connues dans la matrice: 

{{  1/n,    1/n      , ...},
 {... .., A007318, ....},
 {... .., ... ..., ..},
 ... ....,
 {A129687, ... ... ... ... ... ... ..},
 {A131084, A028326 ... ... ... ... ..},
 {A028326, A131084 , A129687 ... ....}}

vous pouvez trouver ces séquences (dans certains cas avec des signes différents) dans le merveilleux http://oeis.org /

Résoudre le problème général est plus difficile, mais j'espère que ce est un début

55
répondu Dr. belisarius 2011-07-21 04:50:17

l '"erreur commune" que vous mentionnez est mélangée par des transpositions aléatoires. Ce problème a été étudié en détail par Diaconis et Shahshahani dans générant une permutation aléatoire avec des transpositions aléatoires (1981) . Ils font une analyse complète des temps d'arrêt et de convergence à l'uniformité. Si vous ne pouvez pas obtenir un lien vers le journal, alors s'il vous plaît envoyez-moi un e-mail et je peux vous envoyer une copie. C'est en fait une lecture amusante (comme la plupart des journaux de Persi Diaconis).

si le tableau a des entrées répétées, alors le problème est légèrement différent. En tant que plug sans vergogne, ce problème plus général est abordé par moi-même, Diaconis et Soundarajan dans L'Annexe B de une règle empirique pour Riffle Shuffling (2011) .

28
répondu PengOne 2011-07-21 05:10:16

disons

  • a = 1/N
  • b = 1-a
  • b i (k) est la matrice de probabilité après i swaps pour l'élément k th. I. e la réponse à la question "Où se trouve k après i swaps?". Par exemple B 0 (3) = (0 0 1 0 ... 0) et B 1 (3) = (a 0 b 0 ... 0) . Ce que vous voulez est B N (k) pour chaque k.
  • K i est une matrice NxN avec 1S dans la I-E colonne et I-E Ligne, zéros partout ailleurs, E. g:

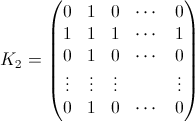
kappa_2

  • je je est la matrice identité, mais avec l'élément x=y=j'ai remis à zéro. E. g pour i=2:

I_2

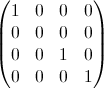
  • Un je est

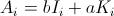
Ai= bIi + aKi

Puis,

B_n

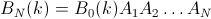
mais parce que B N (k=1..N) forme la matrice d'identité, la probabilité que tout élément donné i sera à la fin à la position j est donnée par l'élément de matrice (i, j) de la matrice:

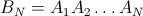
solution matrix

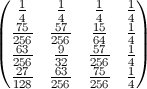
par exemple, pour N=4:

B_4

sous forme de diagramme pour N = 500 (les niveaux de couleur sont 100*probabilité):

B_500

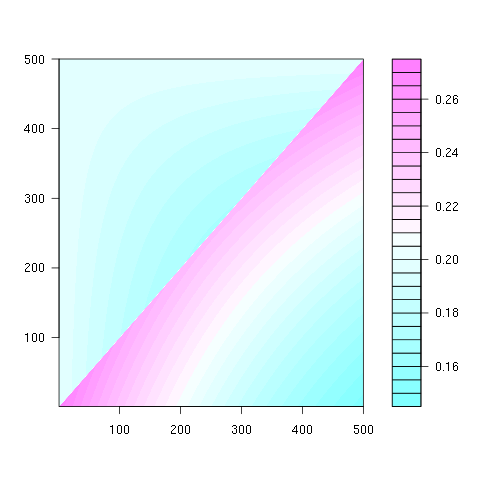
le schéma est le même pour tous les N>2:

  • la "position finale la plus probable pour l'élément k est k-1 .
  • la la " moins probable position finale est k pour k < n*ln (2) , position 1 autrement
15
répondu Eelvex 2011-03-22 02:58:30

je savais que j'avais déjà vu cette question auparavant...

pourquoi ce simple algorithme de mélange produit-il des résultats biaisés? ce qui est une simple raison? " a beaucoup de bonnes choses dans les réponses, en particulier un lien vers une blog de Jeff Atwood sur le code de l'Horreur .

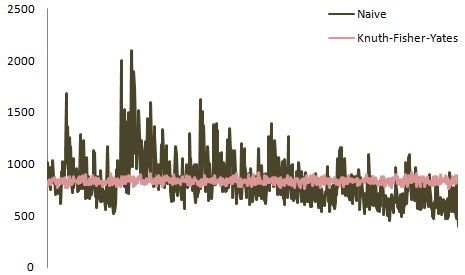
Comme vous pouvez l'avez déjà deviné, basé sur la réponse de @bélisaire, la répartition exacte est très dépendant du nombre d'éléments à mélangées. Voici le tracé D'Atwood pour un pont à 6 éléments:

enter image description here

13
répondu oosterwal 2017-05-23 12:26:23

Quelle belle question! Je voudrais avoir une réponse complète.

Fisher-Yates est agréable à analyser car une fois qu'il décide sur le premier élément, il laisse tomber. Le partial peut changer un élément à plusieurs reprises dans et hors de n'importe quel endroit.

nous pouvons l'analyser de la même façon que nous le ferions pour une chaîne de Markov, en décrivant les actions comme des matrices de transition stochastiques agissant linéairement sur les distributions de probabilité. La plupart des éléments sont laissés seuls, la diagonale est habituellement (n-1) / n. Sur le pass k, quand ils ne sont pas laissés seuls, ils sont échangés avec l'élément k, (ou un élément aléatoire si ils sont l'élément k). C'est 1/(n-1) dans la ligne ou la colonne k. L'élément de ligne et de colonne k est également en 1/(n-1). Il est assez facile de multiplier ces matrices ensemble pour k allant de 1 à N.

nous savons que l'élément à la dernière place sera également susceptible d'avoir été à l'origine n'importe où parce que le dernier passage échange la dernière place également probablement avec les autres. De même, le premier élément sera vraisemblablement placé n'importe où. Cette symétrie est due au fait que la transposition inverse l'ordre de multiplication matricielle. En fait, la matrice est symétrique en ce sens que la rangée i est la même que la colonne (n+1 - i). Au-delà de cela, les chiffres ne montrent pas beaucoup de modèle apparent. Ces solutions exactes sont en accord avec les simulations effectuées par belisarius: dans la fente i, la probabilité d'obtenir j diminue au fur et à mesure que j s'élève à i, la valeur la plus faible est i-1, puis elle monte à sa valeur la plus élevée à i et diminue jusqu'à ce que j atteigne N.

Dans Mathematica, j'ai généré chaque étape avec 

 step[k_, n_] := Normal[SparseArray[{{k, i_} -> 1/n, 
                      {j_, k} -> 1/n, {i_, i_} -> (n - 1)/n} , {n, n}]]

(Je ne l'ai trouvé documenté nulle part, mais la première règle de correspondance est utilisée.) La matrice de transition finale peut être calculée avec: 

Fold[Dot, IdentityMatrix[n], Table[step[m, n], {m, s}]]

ListDensityPlot est un outil de visualisation utile.

Modifier (par bélisaire)

juste une confirmation. Le code suivant donne la même matrice que dans la réponse de @Eelvex: 

step[k_, n_] := Normal[SparseArray[{{k, i_} -> (1/n), 
                      {j_, k} -> (1/n), {i_, i_} -> ((n - 1)/n)}, {n, n}]];
r[n_, s_] := Fold[Dot, IdentityMatrix[n], Table[step[m, n], {m, s}]];
Last@Table[r[4, i], {i, 1, 4}] // MatrixForm
8
répondu wnoise 2012-06-10 08:30:26

la page de Wikipedia sur le Fisher-Yates shuffle a une description et un exemple de ce qui se passera exactement dans ce cas.

3
répondu Jeremiah Willcock 2011-02-27 03:55:44

vous pouvez calculer la distribution en utilisant matrices stochastiques . Soit la matrice A (i,j) décrire la probabilité de la carte à l'origine à la position i se terminant en position J. Alors le KTH swap a une matrice Ak donnée par Ak(i,j) = 1/N si i == k ou j == k , (la carte en position k peut finir n'importe où et n'importe quelle carte peut finir à la position k avec une probabilité égale), Ak(i,i) = (N - 1)/N pour tous i != k (toutes les autres cartes resteront au même endroit avec probabilité (N-1) / N) et tous les autres éléments zéro.

le résultat du mélange complet est alors donné par le produit des matrices AN ... A1 .

je suppose que vous êtes à la recherche d'une description algébrique des probabilités; vous pouvez en obtenir une en élargissant le produit de matrice ci-dessus, mais il j'imagine qu'il sera assez complexe!

mise à jour: je viens de repérer la réponse équivalente de wnoise ci-dessus! oops...

3
répondu daoudc 2011-03-18 09:32:29

j'ai examiné cela plus en détail, et il s'avère que cette distribution a été étudiée en détail. La raison pour laquelle il est d'intérêt est parce que cet algorithme "cassé" est (ou était) utilisé dans le système de puce RSA.

Dans Traînant par semi-aléatoire des transpositions , Elchanan Mossel, Yuval Peres, et Alistair Sinclair étude de ce et une classe plus générale de mélange. Le résultat de ce document semble être qu'il faut log(n) cassé mélange pour obtenir une distribution quasi aléatoire.

In the bias of three pseudorandom shuffles ( Aequationes Mathematicae , 22, 1981, 268-292), Ethan Bolker et David Robbins analysent ce mélange et déterminent que la distance totale de variation à l'uniformité après un seul passage est de 1, ce qui indique que ce n'est pas très aléatoire du tout. Ils font aussi des analyses asympotiques.

enfin, Laurent Saloff-Coste et Jessica Zuniga a trouvé une belle limite supérieure dans leur étude des chaînes de Markov inhomogènes.

3
répondu PengOne 2012-03-14 21:59:03

cette question appelle une " interactive visual matrix diagram analyse du mélange défectueux mentionné. Un tel outil est sur la page Shuffle? - Pourquoi les comparateurs aléatoires sont mauvais par Mike Bostock.

Bostock a mis en place un excellent outil qui analyse les comparateurs aléatoires. Dans la liste déroulante de cette page, choisissez naïve swap (random Goto random) pour voir l'algorithme cassé et le motif qu'elle produit.

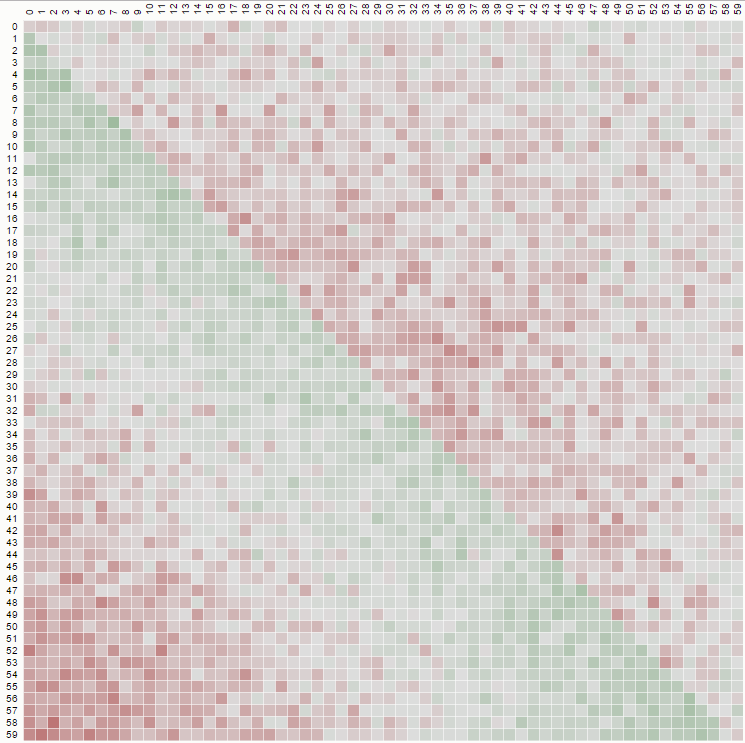
sa page est informative car elle permet de voir les effets immédiats d'un changement de logique sur les données mélangées. Par exemple:

ce diagramme matriciel utilisant un shuffle non uniforme et très biaisé est produit en utilisant un swap naïf (nous choisissons de "1 À N") avec un code comme ceci: 

function shuffle(array) {
    var n = array.length, i = -1, j;
    while (++i < n) {
        j = Math.floor(Math.random() * n);
        t = array[j];
        array[j] = array[i];
        array[i] = t;
    }
}

biased shuffle

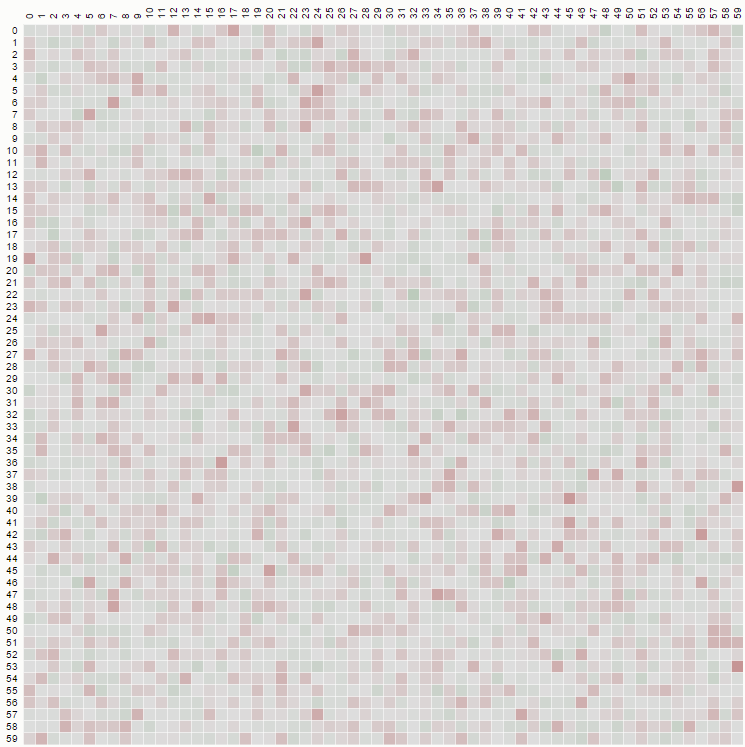
mais si nous implémentons un un mélange non biaisé, où nous choisissons de "k À N" nous devrions voir un diagramme comme celui-ci:

enter image description here

lorsque la distribution est uniforme et qu'elle est produite à partir d'un code tel que: 

function FisherYatesDurstenfeldKnuthshuffle( array ) {
    var pickIndex, arrayPosition = array.length;
    while( --arrayPosition ) {
        pickIndex = Math.floor( Math.random() * ( arrayPosition + 1 ) );
        array[ pickIndex ] = [ array[ arrayPosition ], array[ arrayPosition ] = array[ pickIndex ] ][ 0 ];
    }
}
2
répondu Mac 2017-01-26 19:43:56

les excellentes réponses données jusqu'à présent se concentrent sur la distribution, mais vous avez aussi demandé "que se passe-t-il si vous faites cette erreur?" - ce que je n'ai pas encore vu répondu, donc je vais donner une explication sur ce:

l'algorithme Knuth-Fisher-Yates shuffle choisit 1 des N éléments, puis 1 des N-1 éléments restants et ainsi de suite.

vous pouvez l'implémenter avec deux tableaux a1 et a2 où vous supprimez un élément de a1 et l'insérer dans a2, mais l'algorithme le fait en place (ce qui signifie, qu'il n'a besoin que d'un tableau), comme est expliqué ici (Google: "shuffling Algorithms Fisher-Yates DataGenetics") très bien.

si vous ne retirez pas les éléments, ils peuvent être choisis de nouveau au hasard, ce qui produit le caractère aléatoire biaisé. C'est exactement ce que le 2ème exemple de votre description. Le premier exemple, L'algorithme de Knuth-Fisher-Yates, utilise variable de curseur allant de k à N, qui se souvient des éléments déjà pris, évitant ainsi de choisir des éléments plus d'une fois.

1
répondu Matt 2015-03-16 14:49:25