j'ai regardé autour de moi et j'ai vu beaucoup de longues explications. Voici un petit graphique qui pourrait être utile pour résumer:

noter comment la difficulté augmente de haut en bas: tout NP peut être réduit à NP-Complete , et tout NP-Complete peut être réduit à NP-Hard , tout en p (polynomial) temps.

si vous pouvez résoudre une classe plus difficile de problème en temps P, cela signifie que vous avez trouvé comment résoudre tous les problèmes plus faciles dans P Temps (par exemple, proving P = NP, si vous trouvez comment résoudre n'importe quel NP-problème complet dans P temps).

____________________________________________________________
| Problem Type | Verifiable in P time | Solvable in P time | Increasing Difficulty
___________________________________________________________|           |
| P            |        Yes           |        Yes         |           |
| NP           |        Yes           |     Yes or No *    |           |
| NP-Complete  |        Yes           |      Unknown       |           |
| NP-Hard      |     Yes or No **     |      Unknown ***   |           |
____________________________________________________________           V

Notes sur Yes ou No rubriques:

• * Un problème NP qui est aussi P est résoluble en P de temps.
• ** Un problème NP-Difficile qui est aussi NP-Complet est vérifiable dans P temps.
• *** NP-Complet problèmes (dont l'ensemble forme un sous-ensemble de NP-dur. Le reste de NP hard ne l'est pas.

j'ai aussi trouvé ce diagramme très utile pour voir comment tous ces types correspondent les uns aux autres (faites plus attention à la moitié gauche du diagramme).

c'est une réponse très informelle à la question posée.

peut-on écrire 3233 comme le produit de deux autres nombres plus grands que 1? Y a-t-il un moyen de faire le tour des sept ponts de Königsberg sans prendre de pont deux fois? Ces sont des exemples de questions qui partagent un trait commun. Il peut ne pas être évident comment déterminer efficacement la réponse, mais si la réponse est "oui", alors il ya un court et rapide à vérifier preuve. Dans le premier cas, une factorisation non triviale de 51; dans le second, un itinéraire pour marcher sur les ponts (adapté aux contraintes).

Un problème de décision est une collection de questions avec des réponses oui ou non qui ne varient que par un seul paramètre. Disons que le problème COMPOSITE={"est n composite": n est un entier} ou EULERPATH={"est-ce que le graphique G a un chemin D'Euler?": G est finie graphique}.

maintenant, certains problèmes de décision se prêtent à des algorithmes efficaces, sinon évidents. Euler a découvert un algorithme efficace pour les problèmes comme les "sept ponts de Königsberg" il y a plus de 250 ans.

d'un autre côté, pour de nombreux problèmes de décision, il n'est pas évident comment obtenir la réponse -- mais si vous connaissez quelques informations supplémentaires, il est évident comment aller à prouver que vous avez la bonne réponse. COMPOSITE est comme ceci: Trial division est le algorithme évident, et c'est lent: pour factoriser un nombre de 10 chiffres, vous devez essayer quelque chose comme 100.000 diviseurs possibles. Mais si, par exemple, quelqu'un vous dit que 61 est un diviseur de 3233, simple division longue est un moyen efficace de voir qu'ils sont corrects.

La classe de complexité NP est la classe des problèmes de décision où le " oui " des réponses courtes à l'état, rapide pour vérifier les preuves. Comme COMPOSITE. Un point important est que cette la définition ne dit pas à quel point le problème est difficile. Si vous avez une façon correcte et efficace de résoudre un problème de décision, il suffit de noter les étapes dans la solution est une preuve suffisante.

Algorithmes la recherche continue, et de nouveaux algorithmes intelligents sont créés tout le temps. Un problème que vous pourriez ne pas savoir comment résoudre efficacement aujourd'hui peut s'avérer efficace (pas si évident), la solution de demain. En fait, il a fallu chercheurs jusqu'à 2002 pour trouver une solution efficace au COMPOSITE! Avec toutes ces avancées, il faut vraiment se poser la question: Est-ce que c'est juste une illusion d'avoir des épreuves courtes? Peut-être chaque problème de décision qui se prête à des preuves efficaces a une solution efficace? Personne ne sait .

peut-être la plus grande contribution à ce domaine est venue avec la découverte d'une classe particulière de problèmes NP. En jouant avec des modèles de circuits pour calcul, Stephen Cook a trouvé un problème de décision de la variété NP qui était provably aussi dur ou plus dur que chaque autre problème NP. Une solution efficace pour le booléen problème de satisfaction pourrait être utilisée pour créer une solution efficace à tout autre problème dans NP. Peu après, Richard Karp a montré qu'un certain nombre d'autres problèmes de décision pouvaient servir le même but. Ces problèmes, en un sens, le "noyau dur" problèmes dans NP, est devenu connu sous le nom NP-complete problèmes.

bien sûr, NP est seulement une classe de problèmes de décision. Beaucoup de problèmes ne sont pas énoncés naturellement de cette manière: "trouver les facteurs de N", "trouver le chemin le plus court dans le graphe G qui visite chaque vertex", "donner un ensemble d'assignations variables qui rend l'expression booléenne suivante vraie". Bien qu'on puisse parler officieusement de certains de ces problèmes étant "en NP", techniquement cela ne fait pas beaucoup de sens -- ils ne sont pas des problèmes de décision. Certains de ces problèmes pourraient même avoir le même genre de pouvoir qu'un problème NP-complet: une solution efficace à ces problèmes (non-décision) mènerait directement à une solution efficace à tout problème NP. Un problème comme celui-ci est appelé NP-dur .

en plus des autres grandes réponses, voici le schéma typique les gens utilisent pour montrer la différence entre NP, NP-complet, et NP-dur:

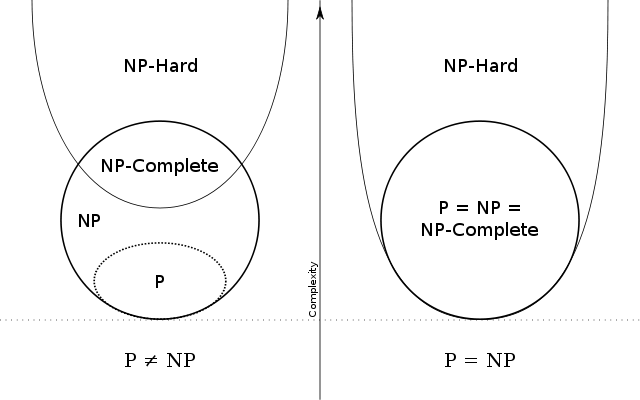
la façon la plus facile d'expliquer P v. NP et tel sans entrer dans les détails techniques est de comparer les" problèmes de mots "avec les"problèmes à choix multiples".

Lorsque vous essayez de résoudre un "problème mot" vous devez trouver la solution à partir de zéro. Lorsque vous tentez de résoudre un "problème à choix multiples", vous avez le choix: soit vous le résolvez comme vous le feriez pour un "problème de mots", soit vous essayez de brancher chacune des réponses qui vous sont données et de choisir la réponse du candidat qui vous convient.

il arrive souvent qu'un" problème à choix multiples "soit beaucoup plus facile que le" problème de mots " correspondant: substituer les réponses du candidat et vérifier si elles conviennent peut exiger beaucoup moins d'effort que de trouver la bonne réponse à partir de zéro.

maintenant, si nous sommes d'accord sur l'effort qui prend le temps polynomial "facile" alors la classe P serait composée de "easy word problems", et la classe NP serait composée de "easy multiple choice problems".

L'essence de P v. NP est la question: "Est-il facile à choix multiples problèmes qui ne sont pas facile comme mot de problèmes"? Autrement dit, y a-t-il des problèmes pour lesquels il est facile de vérifier la validité d'une réponse donnée, mais trouver cette réponse à partir de Zéro est difficile?

maintenant que nous comprenons intuitivement ce qu'est NP, nous devons remettre en question notre intuition. Il s'avère qu'il y a des "choix multiples problèmes" que, dans un certain sens, sont plus difficiles d'entre eux tous: si l'on pouvait trouver une solution à l'un de ces problèmes "les plus durs", on pourrait trouver une solution à tous les problèmes NP! Quand Cook l'a découvert il y a 40 ans, c'était une surprise totale. Ces" plus durs d'entre eux tous " problèmes sont connus comme NP-dur. Si vous trouvez une "solution de problème de mot" à l'un d'eux, vous trouverez automatiquement une "solution de problème de mot" à chaque "problème de choix multiple facile"!

Enfin, NP-complet problèmes sont ceux qui sont simultanément NP et NP-dur. Suivant notre analogie, ils sont à la fois "faciles comme des problèmes à choix multiples" et "les plus durs comme des problèmes de mots".

P (temps Polynomial) : comme son nom l'indique, ce sont les problèmes qui peuvent être résolus en temps polynomial.

NP (Non-deterministic-polynomial Time) : Ce sont les problèmes de décision qui peuvent être vérifiés en temps polynomial. Cela signifie que, si je prétends qu'il existe une solution polynomiale de temps pour un problème particulier, vous me demandez de le prouver. Ensuite, je vais vous donner une preuve que vous pouvez facilement vérifier en temps polynomial. Ces types de problèmes sont appelés NP problème. Notez que, Ici, nous ne parlons pas de savoir s'il existe une solution de temps polynomial pour ce problème ou non. Mais il s'agit de vérifier la solution à un problème donné en temps polynomial.

NP-dur : ceux-ci sont au moins aussi dur que les problèmes les plus difficiles dans NP. Si nous pouvons résoudre ces problèmes en temps polynomial, on peut résoudre n'importe quel problème NP qui peuvent éventuellement exister. Notez que ces problèmes ne sont pas nécessairement des problèmes NP. Cela signifie que nous pouvons / pouvons-ne pas vérifier la solution à ces problèmes en temps polynomial.

NP-Complete: Ce sont les problèmes qui sont à la fois NP et NP-Hard. Cela signifie que, si nous pouvons résoudre ces problèmes, nous pouvons résoudre tout autre problème NP et les solutions à ces problèmes peuvent être vérifiées en temps polynomial.

je pense que nous pouvons y répondre de façon beaucoup plus succincte. J'ai répondu à une question connexe , et j'ai copié ma réponse de là

mais d'abord, un problème NP-hard est un problème pour lequel nous ne pouvons pas prouver qu'il existe une solution de temps polynomiale. NP-dureté d'un " problème-P "est généralement prouvé en convertissant un problème NP-hard déjà prouvé en" Problème-P " dans le temps polynomial.

pour répondre au reste de la question, vous devez d'abord comprendre quels problèmes NP-hard sont aussi NP-complete. Si un problème NP-hard appartient à set NP, alors il est NP-complete. Pour appartenir à l'ensemble NP, un problème doit être

(i) un problème de décision,

(ii) le nombre de solutions au problème devrait être fini et chaque solution devrait être de longueur polynomiale, et

(iii) étant donné une solution de longueur polynomiale, nous devrions être en mesure de dire si la la réponse au problème est oui / non

maintenant, il est facile de voir qu'il pourrait y avoir beaucoup de NP-problèmes difficiles qui n'appartiennent pas à NP fixé et sont plus difficiles à résoudre. Comme un exemple intuitif, l'optimisation-version de voyageur de commerce où nous avons besoin de trouver un horaire réel est plus difficile que la décision-version de voyageur de commerce où nous avons juste besoin de déterminer si un horaire avec la longueur <= k existe ou non.

NP-complet problèmes sont ces problèmes qui sont à la fois un problème NP-Difficile et dans la classe de complexité NP. Donc, pour montrer que tout problème est NP-complet, vous devez montrer que le problème est à la fois dans NP et qu'il est NP-dur.

les problèmes qui appartiennent à la classe de complexité NP peuvent être résolus de façon non déterministe en temps polynomial et une solution possible (c.-à-d. un certificat) pour un problème en NP peut être vérifiée pour l'exactitude en temps polynomial.

un exemple de solution non déterministe au problème de K-clique serait quelque chose comme:

1) Sélectionner au hasard des noeuds k à partir d'un graphe

2) vérifier que ces noeuds k forment une clique.

la stratégie ci-dessus est polynomiale dans la taille du graphe d'entrée et donc le problème de K-clique est en NP.

noter que tous les problèmes déterministiquement solubles en temps polynomial sont aussi en NP.

montrer qu'un problème est NP-hard implique généralement une réduction d'un autre problème NP-hard à votre problème à l'aide d'un polynôme de cartographie du temps: http://en.wikipedia.org/wiki/Reduction_ (complexité)

il y a vraiment de belles réponses pour cette question particulière, donc il n'y a pas de raison d'écrire ma propre explication. Je vais donc essayer de contribuer avec une excellente ressource sur les différentes classes de complexité de calcul.

Pour quelqu'un qui pense que la complexité de calcul est uniquement à propos de P et NP, c'est là la plus exhaustive de ressources à propos de différentes de calcul de la complexité des problèmes. En dehors des problèmes demandés par L'OP, il a énuméré environ 500 classes différentes de problèmes de calcul avec de belles descriptions et aussi la liste des documents de recherche fondamentale qui décrivent la classe.

si je comprends bien, un np-dur le problème n'est pas "plus" qu'un np-complet problème. En fait, par définition, chaque np - problème complet est:

1. NP
2. np-dur

-- Intro. des Algorithmes (3ed) par Cormen, Leiserson, Rivest et Stein, p. 1069