Quels algorithmes puis-je utiliser pour le niveau de volume audio? [fermé]
disons que j'ai un curseur qui peut aller entre 0 et 1. SoundTransform.volume varie également entre 0 (silencieux) et 1 (plein volume), mais si j'utilise une fonction linéaire, disons SoundTransform.volume = slider.volume, le résultat est plutôt pas agréable.
je n'ai pas étudié l'oreille humaine, mais j'ai entendu une fois que la perception humaine est logarithmique, ou quelque chose de similaire. Quels algorithmes dois-je utiliser pour définir le SoundTransform.volume?
8 réponses
la perception humaine en général est logarithmique, aussi quand il s'agit de choses comme la luminosité, etc. ... cela nous permet d'enregistrer de petits changements à de petits "signaux d'entrée" de notre environnement, ou de le dire autrement: pour toujours percevoir un changement d'une quantité physique perceptible par rapport à sa valeur ...
ainsi, vous devriez modifier le volume pour qu'il croisse de façon exponentielle, comme ceci:
y = (Math.exp(x)-1)/(Math.E-1)
vous pouvez essayer d'autres bases:
y = (Math.pow(base,x)-1)/(base-1)
le plus grand la valeur de base est, plus l'effet est fort, plus le volume commence à croître lentement au début et plus il croît rapidement à la fin ...
une approche légèrement plus simple, vous donnant des résultats similaires (vous êtes seulement dans l'intervalle entre 0 et 1, donc les approximations sont assez simples, en fait), est d'exponantier la valeur originale, comme
y = Math.pow(x, exp);
pour exp plus grand que 1, l'effet est que la sortie (c.-à-d. le volume dans votre cas) Monte d'abord plus lentement, puis plus vite vers la fin ... ceci est très similaire aux fonctions exponentielles ... le plus gros exp, plus l'effet est fort ...
greetz
back2dos
audition Humaine est logarithmique, donc, vous voulez une fonction exponentielle (l'inverse) à appliquer à la sortie linéaire de votre curseur. Je ne sais pas si l'oreille humaine est plus proche de ln ou log:
Pour Ln:
e^x
Log:
10^x
vous pourriez expérimenter avec d'autres bases aussi. Vous devrez ensuite à l'échelle de votre sortie de sorte qu'il couvre la gamme de valeurs.
mise à Jour
Après un peu de recherche il semble que la base 2 serait appropriée puisque la puissance est liée au carré de la pression. Si quelqu'un sait, merci de me corriger.
je pense que ce que vous voulez, c'est:
v' = 2^v.a^v - 1
a = ( 2^(log2(m+1)/n) )/2
v est votre valeur d'entrée linéaire allant de 0..et v' est votre valeur logarithmique allant de 0..m
Le -1 dans la première équation est de vous donner une plage de sortie de 0 au lieu de 1 (puisque k^0=1).
Le m+1 est de compenser pour cela vous obtenez 0..m non 0..m+1
vous pouvez bien sûr adapter cela à vos besoins.
L'Audition est compliquée, la sonie perçue varie selon la fréquence, la durée de l'échantillon, et de personne à personne. Donc cela ne peut pas être résolu mathématiquement mais en essayant une variété de fonctions pour le contrôle et en choisissant celui qui "sent" le meilleur.
vous vous trouvez au moment de la variable de contrôle à la fin basse de la gamme, a peu d'effet sur le volume apparent, mais que le volume augmente rapidement à l'extrémité supérieure de la gamme? Ou avez-vous entendre l'inverse, le volume varie trop rapidement à l'extrémité basse et pas assez dans le haut de gamme? Ou voulez-vous un contrôle plus fin sur le volume à des niveaux moyens?
sensibilité accrue aux faibles volumes:
SoundTransform.volume = Math.sin(x * Math.PI / 2);
augmentation de la sensibilité au volume élevé:
SoundTransform.volume = (Math.pow(base,x) - 1)/(base-1);
ou
SoundTransform.volume = Math.pow(x, base);
base > 1, essayer différentes valeurs et de voir comment il se sent. Ou plus drastiquement, un arc circulaire de 90 degrés:
SoundTransform.volume = 1 - Math.sqrt(1-(x * x));
où x est slider.volume et se situe entre 0 et 1.
s'il vous Plaît ne laissez-nous savoir comment vous vous y prenez!
Oui, la perception humaine est logarithmique. Compte tenu de cela, vous devriez ajuster un volume exponentiellement, de sorte que l'augmentation percivée devient linéaire. Voir décibels sur Wikipédia
Android fait déjà de telles choses à partir du cadre Audio.Il utilise des décibels pour ajuster les volumes. L'utilisateur peut utiliser des étapes telles que de 1 à 7 pour la sonnerie ou de 1 à 15 pour la musique. La formule est la suivante:
appel utilisateur réglez L'API de volume de façon linéaire mais obtenez l'amplitude de façon exponentielle. le graphique ci-dessous:
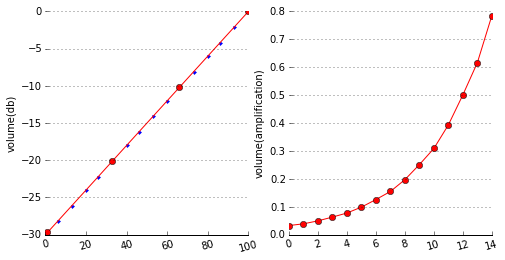
Une augmentation de 3db signifie que vous doublez le volume, mais l'oreille humaine exige ~6db augmentation perçoivent un doublement du volume.
cependant, une courbe strictement logarithmique, tout en modélisant avec précision la perception humaine du volume, a un problème d'utilisabilité.
Quand les gens veulent un fort volume, le bouton devient trop sensible à l'extrémité supérieure, ce qui rend difficile de trouver le "bon" volume.
vous avez probablement déjà eu ce problème auparavant... Sept est trop doux, 8 est trop fort, pendant ce temps 1-3 sont inaudibles sur le bruit de fond.
donc, je recommande une échelle logarithmique, mais avec un plancher à l'extrémité inférieure et un genou doux au sommet pour permettre un plus
Oh, et assurez-vous que le bouton monte à 11. ;)
l'oreille humaine perçoit effectivement des sons sur une échelle logarithmique d'intensité croissante, et pour cette raison, l'unité généralement utilisée pour mesurer l'intensité acoustique est le décibel (qui est en fait utilisé pour toutes sortes d'intensités et de puissances, pas seulement celles du son, et se trouve être une unité sans dimension). Le niveau de référence, 0 dB, est habituellement fixé à la limite inférieure de l'ouïe humaine, et chaque augmentation de dix décibels au-dessus de cette limite équivaut à une augmentation de puissance d'un facteur de 10.
notez, cependant, que vous devriez d'abord vérifier avec d'autres personnes et voir ce qu'ils pensent, juste au cas où; ce qui semble étrange à vous ne peut pas sembler étrange aux autres. S'ils sont d'accord avec toi, Alors vas-y et fais-le de façon exponentielle, mais si tu es dans la minorité, alors il se pourrait que ce soient tes propres oreilles qui soient le problème.
EDIT: Ignore mon troisième paragraphe précédent. Reportez-vous à la réponse de back2dos si vous décidez de le faire de façon exponentielle.
C'est une fonction javascript que j'ai pour une échelle logarithmique pour les dbm. L'entrée est un pourcentage (0.00 à 1.00) et la valeur max (mon implémentation utilise 12db)
le point médian est fixé à 0.5 et cela sera 0db.
quand le pourcentage est zéro, la sortie est l'infini négatif.
function percentageToDb(p, max) {
return max * (1 - (Math.log(p) / Math.log(0.5)));
};
