La distribution de Weibull et les données dans la même figure (avec numpy et scipy) [fermé]
Voici mes données: https://www.dropbox.com/s/xx02015pbr484es/Book2.xlsx
C'est ma sortie:
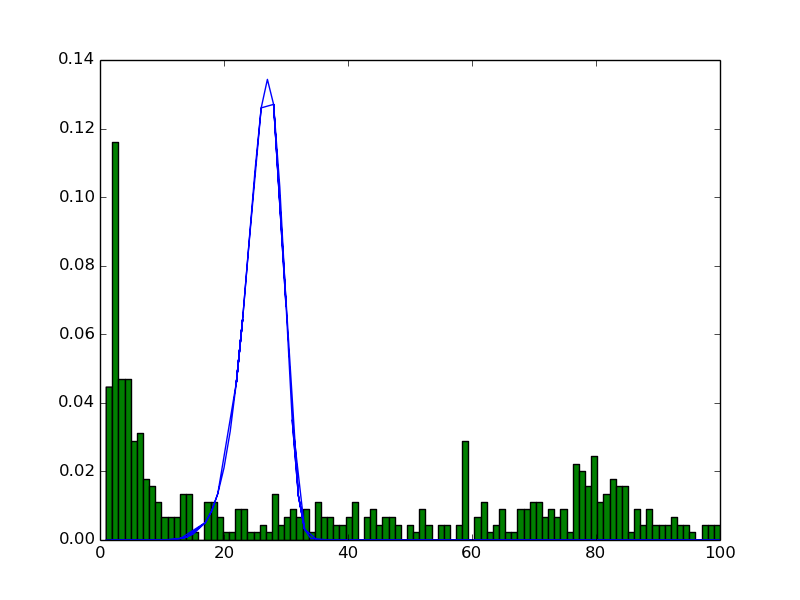
Et c'est la sortie désirée:
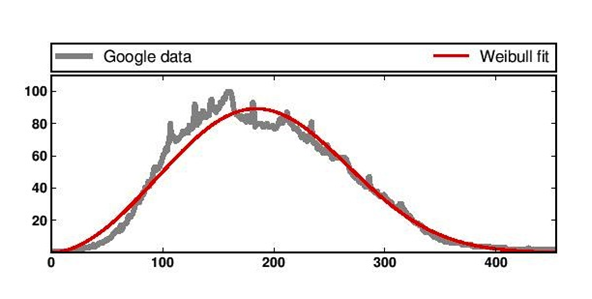
comme vous pouvez le voir,je veux" les données "et la" distribution de Weibull " ensemble, (dans la même figure).
C'est mon code:
(loc, scale) = s.exponweib.fit_loc_scale(mydata, 0.5, 0.5)
print loc, scale
x = np.linspace(mydata.min(), mydata.max(), 1000)
plt.plot(mydata, weib(mydata, loc, scale))
plt.hist(mydata, mydata.max(), normed=True)
plt.show()
1 réponses
tout d'abord, je pense que vous voulez corriger location mais pas scale . (Ainsi scale et shape peuvent changer).
Deuxièmement, je pense (pas sûr à 100%) que vous ne pouvez pas avoir 0 dans vos données pour Weibull (sauf si vous codez une classe Weibull vous-même), donc j'ai changé votre 0 à une petite valeur 1e-8 .
>>> xdata=array([1e-8,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,3,3,3,3,3,3,4,4,4,5,4,4,5,5,6,6,6,6,7,7,8,8,8,9,9,10,11,12,13,13,14,14,13,17,14,15,17,18,18,19,22,23,22,23,24,26,28,32,33,32,31,33,34,37,36,40,40,41,44,41,44,45,47,52,53,51,52,52,53,55,56,59,61,62,65,63,68,69,80,71,71,72,71,69,70,70,71,72,73,75,74,74,75,76,74,79,77,77,77,84,92,88,79,81,81,83,84,88,87,84,84,85,85,85,94,95,91,89,90,87,89,89,90,93,92,93,96,95,98,99,100,99,100,98,94,89,87,86,85,85,84,85,83,83,84,83,81,85,83,83,81,84,93,91,78,79,80,80,80,80,80,78,79,78,79,80,78,78,78,78,79,77,77,77,78,80,82,83,82,80,82,82,83,87,82,82,80,80,79,77,77,77,77,75,75,73,71,73,73,70,72,69,70,70,78,81,69,68,68,68,65,64,66,65,64,62,62,62,62,67,65,61,61,59,58,59,59,59,59,59,59,59,59,59,59,59,58,56,55,52,50,50,48,48,47,46,46,45,44,44,43,43,43,41,41,41,46,47,40,39,39,38,37,37,38,36,35,35,35,35,36,35,33,33,32,31,31,31,29,29,28,28,28,28,30,30,30,28,27,26,25,23,22,23,22,21,20,19,19,18,18,18,17,17,17,14,14,13,13,14,13,12,12,11,11,10,10,9,9,9,8,8,8,8,7,7,7,7,7,7,6,6,6,6,6,6,6,6,6,6,5,5,5,5,5,5,5,5,5,5,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2])
>>> stats.exponweib.fit(xdata, floc=0, f0=1)
(1, 0.87120924706137459, 0, 35.884593247790207)
>>> stats.weibull_min.fit(xdata, floc=0)
(0.87120924706137459, 0, 35.884593247790036)
>>> p0, p1, p2=stats.weibull_min.fit(xdata, floc=0)
>>> ydata=stats.weibull_min.pdf(linspace(0, 120, 100), p0, p1, p2)
>>> plt.hist(xdata, 25, normed=True)
>>> plt.plot(linspace(0, 120, 100), ydata, '-')
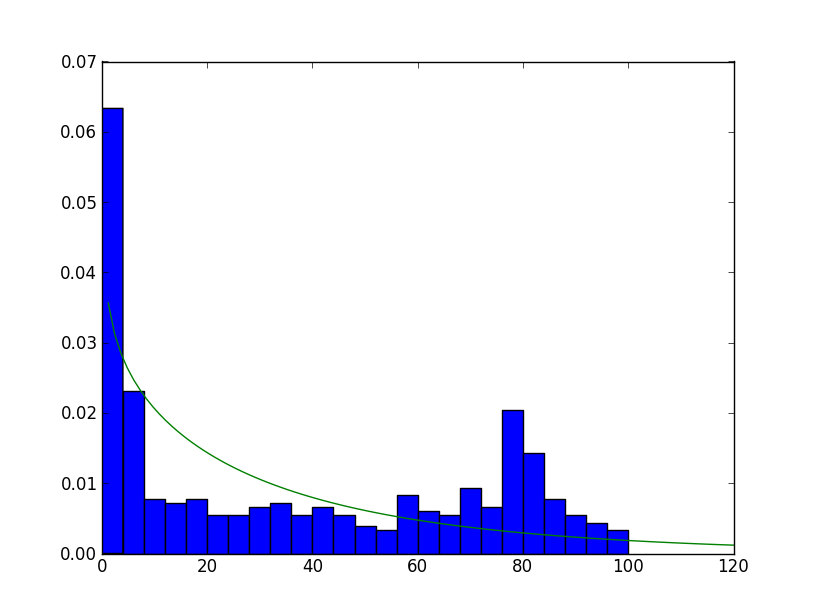
L'ajustement est fait corriger. Il semble laid mais il est dû une grande partie de vos données est petit.
enfin, je soupçonne que vos données originales sont déjà des données de fréquence et non des données brutes, est-ce le cas? (Supposons que vos données ne soient pas censurées par intervalle, ce qui nécessitera un peu de hardcode)
>>> import itertools
>>> x2data=list(itertools.chain(*[[i,]*val for i, val in enumerate(xdata)]))
>>> p0, p1, p2=stats.weibull_min.fit(x2data, floc=0)
>>> y2data=stats.weibull_min.pdf(linspace(0, 500, 100), p0, p1, p2)
>>> plt.plot(linspace(0, 500, 100), y2data, '-')
[<matplotlib.lines.Line2D object at 0x0360B6B0>]
>>> r1,r2,r3=plt.hist(x2data, bins=60, normed=True)
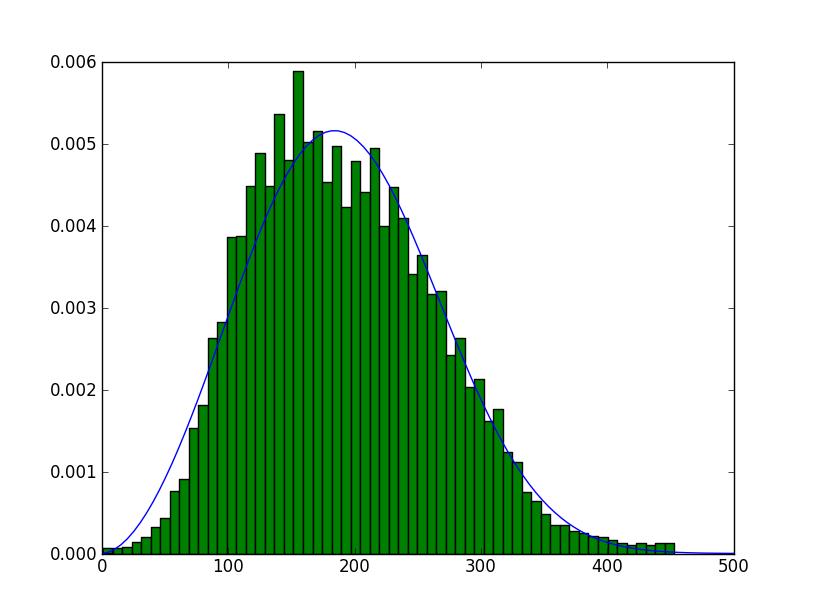Maintenant, le résultat semble beaucoup plus raisonnable. Bien qu'il ne semble pas encore être très distribué Weibull. Plus comme http://en.wikipedia.org/wiki/Shifted_Gompertz_distribution .
mise à Jour: oui, si vous avez 0 dans vos données, vous serez quand vous appelez fit méthodes ( scipy 0.12.0):
Warning (from warnings module):
File "C:\Python27\lib\site-packages\scipy\optimize\optimize.py", line 438
and numpy.max(numpy.abs(fsim[0] - fsim[1:])) <= ftol):
RuntimeWarning: invalid value encountered in subtract