La vectorisation de la Kinect dans le monde réel de coordonner l'algorithme de traitement pour la vitesse

j'ai récemment commencé à travailler avec le V2 Kinect sur Linux avec pylibfreenect2.

lorsque j'ai pu montrer pour la première fois les données du cadre de profondeur dans un nuage de points, j'ai été déçu de voir qu'aucun des pixels de profondeur ne semblait se trouver à la bonne position.

Vue Latérale d'une pièce (notez que le plafond est courbé).

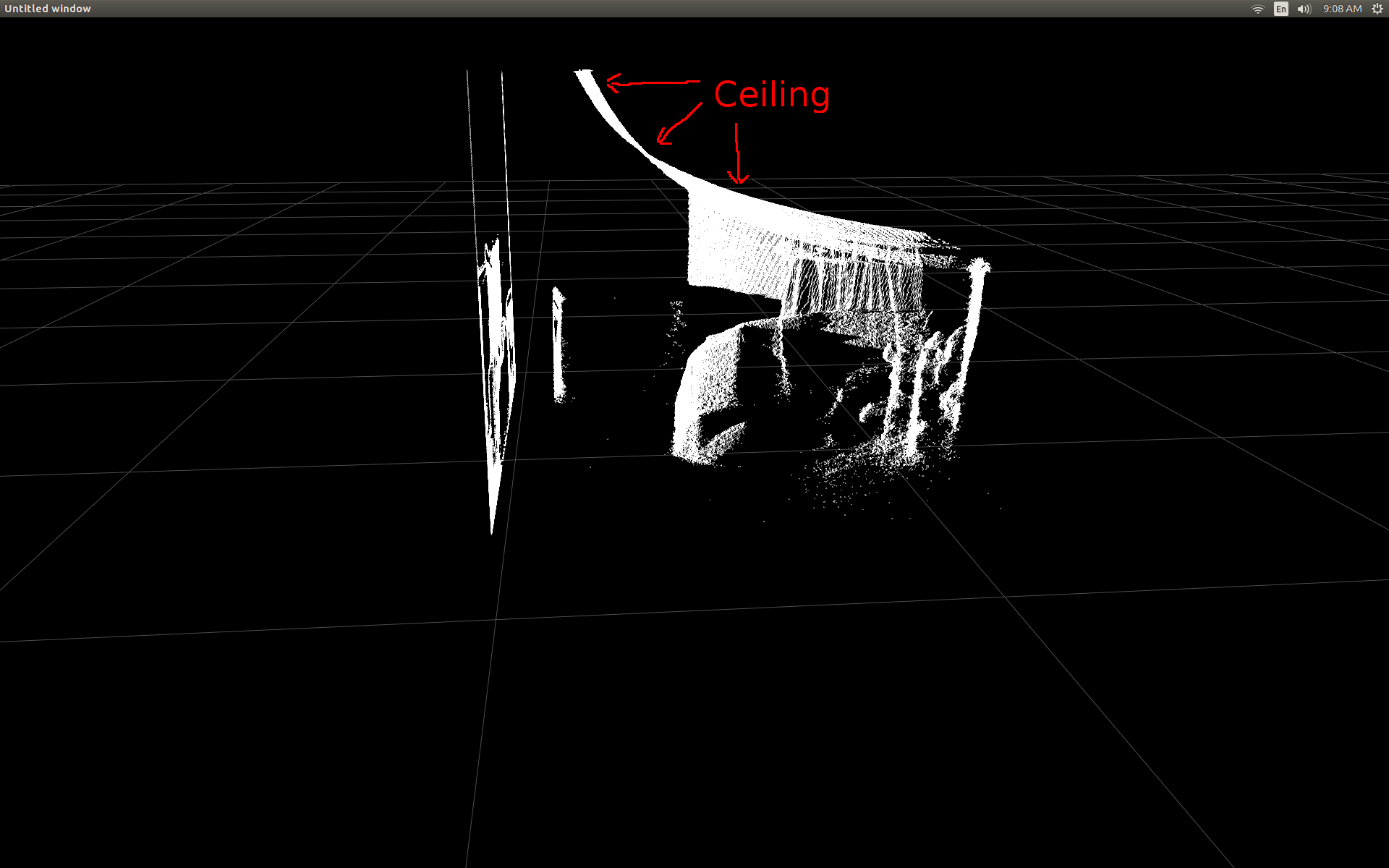
j'ai fait quelques recherches et j'ai réalisé qu'il y avait une trigonométrie simple pour faire le conversion.

Pour tester, j'ai commencé avec un pré-écrite fonction dans pylibfreenect2 qui accepte une colonne, une ligne et d'une profondeur de pixel d'intensité renvoie alors que le pixel de la situation actuelle:

X, Y, Z = registration.getPointXYZ(undistorted, row, col)

Ce n'est un étonnamment bon travail à corriger les positions:

le seul inconvénient à utiliser getPointXYZ () ou getPointXYZRGB () c'est qu'ils travaillent sur un seul pixel à temps. Cela peut prendre un certain temps en Python car il nécessite l'utilisation de boucles-For imbriquées comme so:

n_rows = d.shape[0]
n_columns = d.shape[1]
out = np.zeros((n_rows * n_columns, 3), dtype=np.float64)
for row in range(n_rows):
    for col in range(n_columns):
        X, Y, Z = registration.getPointXYZ(undistorted, row, col)
        out[row * n_columns + col] = np.array([Z, X, -Y])

j'ai essayé de mieux comprendre comment getPointXYZ() calculait une coordonnée. Au meilleur de mes connaissances, il ressemble à cette fonction OpenKinect-for-Processing: depthToPointCloudPos (). bien que je soupçonne la version de libfreenect2 a plus de choses en cours sous le capot.

en utilisant ce code source gitHub comme exemple j'ai ensuite essayé de le ré-écrire en Python pour mes propres expériences et en est venu whth la suivante:

#camera information based on the Kinect v2 hardware
CameraParams = {
  "cx":254.878,
  "cy":205.395,
  "fx":365.456,
  "fy":365.456,
  "k1":0.0905474,
  "k2":-0.26819,
  "k3":0.0950862,
  "p1":0.0,
  "p2":0.0,
}

def depthToPointCloudPos(x_d, y_d, z, scale = 1000):
    #calculate the xyz camera position based on the depth data    
    x = (x_d - CameraParams['cx']) * z / CameraParams['fx']
    y = (y_d - CameraParams['cy']) * z / CameraParams['fy']

    return x/scale, y/scale, z/scale

C'est une comparaison entre le traditionnel getPointXYZ et ma fonction personnalisée:

ils se ressemblent beaucoup. Toutefois, avec des différences apparentes. La comparaison à gauche montre les bords qui sont plus droites aussi une certaine forme sinusoïde sur le plafond plat. Je soupçonne que des calculs supplémentaires sont impliqués.

je serais très intéressé de savoir si quelqu'un a des idées sur ce qui pourrait différer entre ma fonction et getPointXYZ de libfreenect2.

cependant, la principale raison pour laquelle j'ai posté ici est de demander si j'ai essayé de vectoriser la fonction ci-dessus pour travailler sur un tableau entier au lieu de faire une boucle à travers chaque élément.

Appliquer ce que j'ai appris de ce qui précède, j'ai été capable d'écrire une fonction qui semble être une alternative à vectorisé depthToPointCloudPos:

[EDIT]

merci à Benjamin pour avoir rendu cette fonction encore plus efficace!

def depthMatrixToPointCloudPos(z, scale=1000):
    #bacically this is a vectorized version of depthToPointCloudPos()
    C, R = np.indices(z.shape)

    R = np.subtract(R, CameraParams['cx'])
    R = np.multiply(R, z)
    R = np.divide(R, CameraParams['fx'] * scale)

    C = np.subtract(C, CameraParams['cy'])
    C = np.multiply(C, z)
    C = np.divide(C, CameraParams['fy'] * scale)

    return np.column_stack((z.ravel() / scale, R.ravel(), -C.ravel()))

cela fonctionne et produit les mêmes résultats de pointcloud que la fonction précédente depthtpointcloudpos(). La seule différence est que mon taux de traitement est passé de ~1 Fps à 5-10 Fps (WhooHoo!). Je crois que cela élimine un goulot de bouteille causé par Python faisant tous les calculs. Donc mon scatterplot fonctionne maintenant en douceur encore une fois avec les coordonnées semi-réelles calculées.

maintenant que j'ai une fonction efficace pour extraire les coordonnées 3d du cadre de profondeur, j'aimerais vraiment appliquer cette approche à la cartographie des données de la caméra couleur à mes pixels de profondeur. Cependant, je ne suis pas sûr de ce que les mathématiques ou les variables sont impliqués pour faire cela, et il n'y avait pas beaucoup de mention sur la façon de le calculer sur Google.

alternativement j'ai pu utiliser libfreenect2 pour mapper les couleurs à ma profondeur de pixels à l'aide de getPointXYZRGB:

#Format undistorted and regisered data to real-world coordinates with mapped colors (dont forget color=out_col in setData)
n_rows = d.shape[0]
n_columns = d.shape[1]
out = np.zeros((n_rows * n_columns, 3), dtype=np.float64)
colors = np.zeros((d.shape[0] * d.shape[1], 3), dtype=np.float64)
for row in range(n_rows):
    for col in range(n_columns):
        X, Y, Z, B, G, R = registration.getPointXYZRGB(undistorted, registered, row, col)
        out[row * n_columns + col] = np.array([X, Y, Z])
        colors[row * n_columns + col] = np.divide([R, G, B], 255)
sp2.setData(pos=np.array(out, dtype=np.float64), color=colors, size=2)

produit un pointcloud et des vertex colorés (très lent <1fps):

En résumé mes deux questions sont fondamentalement:

• quelles étapes supplémentaires seraient nécessaires pour que les coordonnées 3d réelles reviennent de mon depthToPointCloudPos () la fonction (et l'implémentation vectorisée) sont plus proches de la les données retournées par getPointXYZ() de libfreenect2?

• et, qu'est-ce que cela impliquerait dans la création d'un moyen (éventuellement vectorisé) pour générer la profondeur de la carte d'enregistrement de couleur dans ma propre application? s'il vous plaît voir la mise à jour car cela a été résolu.

---

[UPDATE]

j'ai réussi à mapper les données de couleur à chaque pixel en utilisant le cadre enregistré. Il était très simple et ne nécessitait l'ajout de ces lignes avant d'appeler la fonction setData():

colors = registered.asarray(np.uint8)
colors = np.divide(colors, 255)
colors = colors.reshape(colors.shape[0] * colors.shape[1], 4 )
colors = colors[:, :3:] #BGRA to BGR (slices out the alpha channel)  
colors = colors[...,::-1] #BGR to RGB

cela permet à Python de traiter rapidement les données couleur et donne des résultats lisses. Je les ai mis à jour/ajoutés à l'exemple fonctionnel ci-dessous.

traitement de coordonnées en temps réel avec enregistrement des couleurs en cours d'exécution en temps réel en Python!

(la résolution de l'image GIF a été grandement réduite)

---

[UPDATE]

après avoir passé un peu plus de temps avec l'application j'ai ajouté quelques paramètres supplémentaires et accordé leurs valeurs avec l'espoir d'améliorer la qualité visuelle du scatter plot et éventuellement rendre les choses plus intuitives pour cet exemple/question.

le plus important est que j'ai placé les vertex pour qu'ils soient opaques:

sp2 = gl.GLScatterPlotItem(pos=pos)
sp2.setGLOptions('opaque') # Ensures not to allow vertexes located behinde other vertexes to be seen.

j'ai alors remarqué que lorsque le zoom était très proche des surfaces, le la distance entre les verts adjacents semble augmenter jusqu'à ce que tout ce qui est visible soit surtout de l'espace vide. Cela s'explique en partie par le fait que la taille des sommets n'a pas changé.

pour aider à créer un viewport" zoom-friendly " plein de Vertex colorés j'ai ajouté ces lignes qui calcule la taille du point de vertex basé sur le niveau de zoom actuel (pour chaque mise à jour):

# Calculate a dynamic vertex size based on window dimensions and camera's position - To become the "size" input for the scatterplot's setData() function.
v_rate = 8.0 # Rate that vertex sizes will increase as zoom level increases (adjust this to any desired value).
v_scale = np.float32(v_rate) / gl_widget.opts['distance'] # Vertex size increases as the camera is "zoomed" towards center of view.
v_offset = (gl_widget.geometry().width() / 1000)**2 # Vertex size is offset based on actual width of the viewport.
v_size = v_scale + v_offset

Et lo et voici:

(Encore une fois, GIF résolution de l'image a été fortement réduite)

peut-être pas aussi bon que de retirer un nuage de points, mais il semble aider à rendre les choses plus faciles en essayant de comprendre ce que vous regardez réellement.

toutes les modifications mentionnées ont été incluses dans la fonctionnalité exemple.

---

[UPDATE]

comme on l'a vu dans les deux animations précédentes, il est clair que le pointcloud des coordonnées du monde réel a une orientation asymétrique par rapport aux axes de la grille. C'est parce que je ne compense pas L'orientation réelle du Kinect dans le vrai mot!

J'ai donc implémenté une fonction trig vectorisée supplémentaire qui calcule une nouvelle coordonnée (rotation et offset) pour chaque vertex. Cette orientale correctement par rapport à la position réelle du Kinect dans l'espace réel. Et est nécessaire lors de l'utilisation de trépieds qui inclinent (peut également être utilisé pour connecter la sortie d'un INU ou gyroscope/accéléromètre de rétroaction en temps réel).

def applyCameraMatrixOrientation(pt):
    # Kinect Sensor Orientation Compensation
    # bacically this is a vectorized version of applyCameraOrientation()
    # uses same trig to rotate a vertex around a gimbal.
    def rotatePoints(ax1, ax2, deg):
        # math to rotate vertexes around a center point on a plane.
        hyp = np.sqrt(pt[:, ax1] ** 2 + pt[:, ax2] ** 2) # Get the length of the hypotenuse of the real-world coordinate from center of rotation, this is the radius!
        d_tan = np.arctan2(pt[:, ax2], pt[:, ax1]) # Calculate the vertexes current angle (returns radians that go from -180 to 180)

        cur_angle = np.degrees(d_tan) % 360 # Convert radians to degrees and use modulo to adjust range from 0 to 360.
        new_angle = np.radians((cur_angle + deg) % 360) # The new angle (in radians) of the vertexes after being rotated by the value of deg.

        pt[:, ax1] = hyp * np.cos(new_angle) # Calculate the rotated coordinate for this axis.
        pt[:, ax2] = hyp * np.sin(new_angle) # Calculate the rotated coordinate for this axis.

    #rotatePoints(1, 2, CameraPosition['roll']) #rotate on the Y&Z plane # Disabled because most tripods don't roll. If an Inertial Nav Unit is available this could be used)
    rotatePoints(0, 2, CameraPosition['elevation']) #rotate on the X&Z plane
    rotatePoints(0, 1, CameraPosition['azimuth']) #rotate on the X&Y plane

    # Apply offsets for height and linear position of the sensor (from viewport's center)
    pt[:] += np.float_([CameraPosition['x'], CameraPosition['y'], CameraPosition['z']])



    return pt

juste une note: rotatePoints () est seulement appelé pour 'elevation' et 'azimuth'. C'est parce que la plupart des trépieds ne supportent pas roll et que pour sauvegarder sur les cycles CPU il a été désactivé par défaut. Si vous avez l'intention de faire quelque chose de fantaisie alors certainement hésitez pas à dé-commentez!!

notez que le plancher de la grille est de niveau dans cette image mais le pointcloud gauche n'est pas aligné avec:

Les paramètres pour définir le Kinect de l'orientation:

CameraPosition = {
    "x": 0, # actual position in meters of kinect sensor relative to the viewport's center.
    "y": 0, # actual position in meters of kinect sensor relative to the viewport's center.
    "z": 1.7, # height in meters of actual kinect sensor from the floor.
    "roll": 0, # angle in degrees of sensor's roll (used for INU input - trig function for this is commented out by default).
    "azimuth": 0, # sensor's yaw angle in degrees.
    "elevation": -15, # sensor's pitch angle in degrees.
}

vous devez les mettre à jour en fonction de la position et de l'orientation réelles de votre capteur:

Les deux plus importants les paramètres sont l'angle thêta (élévation) et la hauteur par rapport au sol. Un simple ruban de mesure et un oeil calibré sont tout ce que j'ai utilisé, mais j'ai l'intention de donner un jour des données encodeur ou INU pour mettre à jour ces paramètres en temps réel (que le capteur est déplacé autour).

encore une fois, tous les changements ont été reflétés dans l'exemple fonctionnel.

---

Si quelqu'un réussit à apporter des améliorations à cet exemple ou a des suggestions pour ce qui est des moyens de rendre les choses plus compactes, j'apprécierais beaucoup que vous laissiez un commentaire expliquant les détails.

Voici l'exemple entièrement fonctionnel de ce projet:

#! /usr/bin/python

#--------------------------------#
# Kinect v2 point cloud visualization using a Numpy based 
# real-world coordinate processing algorithm and OpenGL.
#--------------------------------#

import sys
import numpy as np

from pyqtgraph.Qt import QtCore, QtGui
import pyqtgraph.opengl as gl

from pylibfreenect2 import Freenect2, SyncMultiFrameListener
from pylibfreenect2 import FrameType, Registration, Frame, libfreenect2

fn = Freenect2()
num_devices = fn.enumerateDevices()
if num_devices == 0:
    print("No device connected!")
    sys.exit(1)

serial = fn.getDeviceSerialNumber(0)
device = fn.openDevice(serial)

types = 0
types |= FrameType.Color
types |= (FrameType.Ir | FrameType.Depth)
listener = SyncMultiFrameListener(types)

# Register listeners
device.setColorFrameListener(listener)
device.setIrAndDepthFrameListener(listener)

device.start()

# NOTE: must be called after device.start()
registration = Registration(device.getIrCameraParams(),
                            device.getColorCameraParams())

undistorted = Frame(512, 424, 4)
registered = Frame(512, 424, 4)


#QT app
app = QtGui.QApplication([])
gl_widget = gl.GLViewWidget()
gl_widget.show()
gl_grid = gl.GLGridItem()
gl_widget.addItem(gl_grid)

#initialize some points data
pos = np.zeros((1,3))

sp2 = gl.GLScatterPlotItem(pos=pos)
sp2.setGLOptions('opaque') # Ensures not to allow vertexes located behinde other vertexes to be seen.

gl_widget.addItem(sp2)

# Kinects's intrinsic parameters based on v2 hardware (estimated).
CameraParams = {
  "cx":254.878,
  "cy":205.395,
  "fx":365.456,
  "fy":365.456,
  "k1":0.0905474,
  "k2":-0.26819,
  "k3":0.0950862,
  "p1":0.0,
  "p2":0.0,
}

def depthToPointCloudPos(x_d, y_d, z, scale=1000):
    # This runs in Python slowly as it is required to be called from within a loop, but it is a more intuitive example than it's vertorized alternative (Purly for example)
    # calculate the real-world xyz vertex coordinate from the raw depth data (one vertex at a time).
    x = (x_d - CameraParams['cx']) * z / CameraParams['fx']
    y = (y_d - CameraParams['cy']) * z / CameraParams['fy']

    return x / scale, y / scale, z / scale

def depthMatrixToPointCloudPos(z, scale=1000):
    # bacically this is a vectorized version of depthToPointCloudPos()
    # calculate the real-world xyz vertex coordinates from the raw depth data matrix.
    C, R = np.indices(z.shape)

    R = np.subtract(R, CameraParams['cx'])
    R = np.multiply(R, z)
    R = np.divide(R, CameraParams['fx'] * scale)

    C = np.subtract(C, CameraParams['cy'])
    C = np.multiply(C, z)
    C = np.divide(C, CameraParams['fy'] * scale)

    return np.column_stack((z.ravel() / scale, R.ravel(), -C.ravel()))

# Kinect's physical orientation in the real world.
CameraPosition = {
    "x": 0, # actual position in meters of kinect sensor relative to the viewport's center.
    "y": 0, # actual position in meters of kinect sensor relative to the viewport's center.
    "z": 1.7, # height in meters of actual kinect sensor from the floor.
    "roll": 0, # angle in degrees of sensor's roll (used for INU input - trig function for this is commented out by default).
    "azimuth": 0, # sensor's yaw angle in degrees.
    "elevation": -15, # sensor's pitch angle in degrees.
}

def applyCameraOrientation(pt):
    # Kinect Sensor Orientation Compensation
    # This runs slowly in Python as it is required to be called within a loop, but it is a more intuitive example than it's vertorized alternative (Purly for example)
    # use trig to rotate a vertex around a gimbal.
    def rotatePoints(ax1, ax2, deg):
        # math to rotate vertexes around a center point on a plane.
        hyp = np.sqrt(pt[ax1] ** 2 + pt[ax2] ** 2) # Get the length of the hypotenuse of the real-world coordinate from center of rotation, this is the radius!
        d_tan = np.arctan2(pt[ax2], pt[ax1]) # Calculate the vertexes current angle (returns radians that go from -180 to 180)

        cur_angle = np.degrees(d_tan) % 360 # Convert radians to degrees and use modulo to adjust range from 0 to 360.
        new_angle = np.radians((cur_angle + deg) % 360) # The new angle (in radians) of the vertexes after being rotated by the value of deg.

        pt[ax1] = hyp * np.cos(new_angle) # Calculate the rotated coordinate for this axis.
        pt[ax2] = hyp * np.sin(new_angle) # Calculate the rotated coordinate for this axis.

    #rotatePoints(0, 2, CameraPosition['roll']) #rotate on the Y&Z plane # Disabled because most tripods don't roll. If an Inertial Nav Unit is available this could be used)
    rotatePoints(1, 2, CameraPosition['elevation']) #rotate on the X&Z plane
    rotatePoints(0, 1, CameraPosition['azimuth']) #rotate on the X&Y plane

    # Apply offsets for height and linear position of the sensor (from viewport's center)
    pt[:] += np.float_([CameraPosition['x'], CameraPosition['y'], CameraPosition['z']])



    return pt

def applyCameraMatrixOrientation(pt):
    # Kinect Sensor Orientation Compensation
    # bacically this is a vectorized version of applyCameraOrientation()
    # uses same trig to rotate a vertex around a gimbal.
    def rotatePoints(ax1, ax2, deg):
        # math to rotate vertexes around a center point on a plane.
        hyp = np.sqrt(pt[:, ax1] ** 2 + pt[:, ax2] ** 2) # Get the length of the hypotenuse of the real-world coordinate from center of rotation, this is the radius!
        d_tan = np.arctan2(pt[:, ax2], pt[:, ax1]) # Calculate the vertexes current angle (returns radians that go from -180 to 180)

        cur_angle = np.degrees(d_tan) % 360 # Convert radians to degrees and use modulo to adjust range from 0 to 360.
        new_angle = np.radians((cur_angle + deg) % 360) # The new angle (in radians) of the vertexes after being rotated by the value of deg.

        pt[:, ax1] = hyp * np.cos(new_angle) # Calculate the rotated coordinate for this axis.
        pt[:, ax2] = hyp * np.sin(new_angle) # Calculate the rotated coordinate for this axis.

    #rotatePoints(1, 2, CameraPosition['roll']) #rotate on the Y&Z plane # Disabled because most tripods don't roll. If an Inertial Nav Unit is available this could be used)
    rotatePoints(0, 2, CameraPosition['elevation']) #rotate on the X&Z plane
    rotatePoints(0, 1, CameraPosition['azimuth']) #rotate on the X&Y

    # Apply offsets for height and linear position of the sensor (from viewport's center)
    pt[:] += np.float_([CameraPosition['x'], CameraPosition['y'], CameraPosition['z']])



    return pt


def update():
    colors = ((1.0, 1.0, 1.0, 1.0))

    frames = listener.waitForNewFrame()

    # Get the frames from the Kinect sensor
    ir = frames["ir"]
    color = frames["color"]
    depth = frames["depth"]

    d = depth.asarray() #the depth frame as an array (Needed only with non-vectorized functions)

    registration.apply(color, depth, undistorted, registered)

    # Format the color registration map - To become the "color" input for the scatterplot's setData() function.
    colors = registered.asarray(np.uint8)
    colors = np.divide(colors, 255) # values must be between 0.0 - 1.0
    colors = colors.reshape(colors.shape[0] * colors.shape[1], 4 ) # From: Rows X Cols X RGB -to- [[r,g,b],[r,g,b]...]
    colors = colors[:, :3:]  # remove alpha (fourth index) from BGRA to BGR
    colors = colors[...,::-1] #BGR to RGB

    # Calculate a dynamic vertex size based on window dimensions and camera's position - To become the "size" input for the scatterplot's setData() function.
    v_rate = 5.0 # Rate that vertex sizes will increase as zoom level increases (adjust this to any desired value).
    v_scale = np.float32(v_rate) / gl_widget.opts['distance'] # Vertex size increases as the camera is "zoomed" towards center of view.
    v_offset = (gl_widget.geometry().width() / 1000)**2 # Vertex size is offset based on actual width of the viewport.
    v_size = v_scale + v_offset

    # Calculate 3d coordinates (Note: five optional methods are shown - only one should be un-commented at any given time)

    """
    # Method 1 (No Processing) - Format raw depth data to be displayed
    m, n = d.shape
    R, C = np.mgrid[:m, :n]
    out = np.column_stack((d.ravel() / 4500, C.ravel()/m, (-R.ravel()/n)+1))
    """

    # Method 2 (Fastest) - Format and compute the real-world 3d coordinates using a fast vectorized algorithm - To become the "pos" input for the scatterplot's setData() function.
    out = depthMatrixToPointCloudPos(undistorted.asarray(np.float32))

    """
    # Method 3 - Format undistorted depth data to real-world coordinates
    n_rows, n_columns = d.shape
    out = np.zeros((n_rows * n_columns, 3), dtype=np.float32)
    for row in range(n_rows):
        for col in range(n_columns):
            z = undistorted.asarray(np.float32)[row][col]
            X, Y, Z = depthToPointCloudPos(row, col, z)
            out[row * n_columns + col] = np.array([Z, Y, -X])
    """

    """
    # Method 4 - Format undistorted depth data to real-world coordinates
    n_rows, n_columns = d.shape
    out = np.zeros((n_rows * n_columns, 3), dtype=np.float64)
    for row in range(n_rows):
        for col in range(n_columns):
            X, Y, Z = registration.getPointXYZ(undistorted, row, col)
            out[row * n_columns + col] = np.array([Z, X, -Y])
    """

    """
    # Method 5 - Format undistorted and regisered data to real-world coordinates with mapped colors (dont forget color=colors in setData)
    n_rows, n_columns = d.shape
    out = np.zeros((n_rows * n_columns, 3), dtype=np.float64)
    colors = np.zeros((d.shape[0] * d.shape[1], 3), dtype=np.float64)
    for row in range(n_rows):
        for col in range(n_columns):
            X, Y, Z, B, G, R = registration.getPointXYZRGB(undistorted, registered, row, col)
            out[row * n_columns + col] = np.array([Z, X, -Y])
            colors[row * n_columns + col] = np.divide([R, G, B], 255)
    """


    # Kinect sensor real-world orientation compensation.
    out = applyCameraMatrixOrientation(out)

    """
    # For demonstrating the non-vectorized orientation compensation function (slow)
    for i, pt in enumerate(out):
        out[i] = applyCameraOrientation(pt)
    """


    # Show the data in a scatter plot
    sp2.setData(pos=out, color=colors, size=v_size)

    # Lastly, release frames from memory.
    listener.release(frames)

t = QtCore.QTimer()
t.timeout.connect(update)
t.start(50)


## Start Qt event loop unless running in interactive mode.
if __name__ == '__main__':
    import sys
    if (sys.flags.interactive != 1) or not hasattr(QtCore, 'PYQT_VERSION'):
        QtGui.QApplication.instance().exec_()

device.stop()
device.close()

sys.exit(0)