dans Matlab, le seul moyen d'obtenir des fonctions vectorisées intégrées à multithread est d'attendre que MathWorks les implémente comme tel.

alternativement, vous pouvez écrire le calcul vectorisé comme une boucle, et les exécuter en parallèle en utilisant parfor .

enfin, un certain nombre de fonctions sont GPU-activé , de sorte qu'avec l'accès à la boîte à outils de traitement en parallèle, vous pouvez paralléliser ces opérations, y compris la soustraction et la puissance par élément.

Vectorisation pour meshgrid et ndgrid

si vous êtes toujours intéressé à trouver une implémentation vectorisée pour rendre le code meshgrid basé dans le problème plus rapide, laissez-moi vous suggérer une méthode vectorisé avec bsxfun et il est GPU version portée. Je crois fermement que les gens doivent considérer vectorization with GPUs comme une option prometteuse pour accélérer les codes MATLAB . Codes qui emploient meshgrid ou ndgrid et dont les sorties doivent être exploité avec un certain fonctionnement élémentaire configuration d'un terrain parfait pour employer bsxfun dans ces codes. Pour ajouter à cela, L'utilisation de GPU avec bsxfun , qui lui permet de travailler sur les éléments indépendamment avec des centaines et des milliers de noyaux CUDA disponibles, le rend juste parfait pour L'implémentation GPU.

Pour votre problème spécifique, les entrées étaient -

x = -2:0.01:2;
y = -2:0.01:2;

ensuite, vous avez eu -

[xx,yy] = meshgrid(x,y);
z = sin(xx.^2-yy.^2);

avec bsxfun , ceci devient un one-liner -

z = sin(bsxfun(@minus,x.^2,y.^2.'));

Benchmarking

GPU analyse comparative des conseils ont été prises à partir de Mesurer et Améliorer les Performances du processeur graphique .

%// Warm up GPU call with insignificant small scalar inputs
temp1 = sin_sqdiff_vect2(0,0);

N_arr = [50 100 200 500 1000 2000 3000]; %// array elements for N (datasize)
timeall = zeros(3,numel(N_arr));

for k = 1:numel(N_arr)
    N = N_arr(k);
    x = linspace(-20,20,N);
    y = linspace(-20,20,N);

    f = @() sin_sqdiff_org(x,y);%// Original CPU code
    timeall(1,k) = timeit(f);
    clear f

    f = @() sin_sqdiff_vect1(x,y);%// Vectorized CPU code
    timeall(2,k) = timeit(f);
    clear f

    f = @() sin_sqdiff_vect2(x,y);%// Vectorized GPU(GTX 750Ti) code
    timeall(3,k) = gputimeit(f);
    clear f
end

%// Display benchmark results
figure,hold on, grid on
plot(N_arr,timeall(1,:),'-b.')
plot(N_arr,timeall(2,:),'-ro')
plot(N_arr,timeall(3,:),'-kx')
legend('Original CPU','Vectorized CPU','Vectorized GPU (GTX 750 Ti)')
xlabel('Datasize (N) ->'),ylabel('Time(sec) ->')

fonctions associées

%// Original code
function z = sin_sqdiff_org(x,y)
[xx,yy] = meshgrid(x,y);
z = sin(xx.^2-yy.^2);
return;

%// Vectorized CPU code
function z = sin_sqdiff_vect1(x,y)
z = sin(bsxfun(@minus,x.^2,y.^2.')); %//'
return;

%// Vectorized GPU code
function z = sin_sqdiff_vect2(x,y)
gx = gpuArray(x);
gy = gpuArray(y);
gz = sin(bsxfun(@minus,gx.^2,gy.^2.')); %//'
z =  gather(gz);
return;

résultats

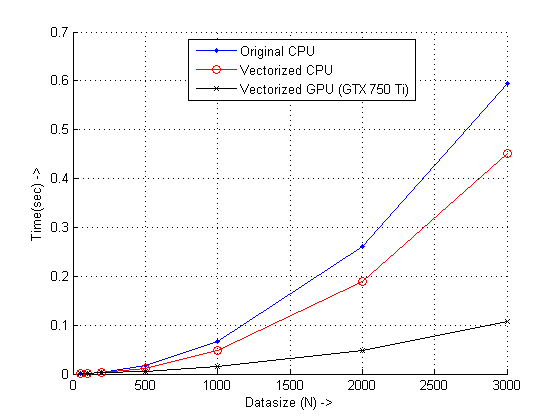
Conclusions

comme le montrent les résultats, la méthode vectorisée avec GPU montre une bonne amélioration de la performance qui est d'environ 4.3x contre le code CPU vectorisé et 6x contre le code original. S'il vous plaît garder à l'esprit que GPU doit surmonter un minimum de frais généraux qui est nécessaire avec sa mise en place, donc au moins une entrée de taille décente est nécessaire pour voir l'amélioration. Avec un peu de chance, les gens pourraient explorer plus de vectorization with GPUs , car il ne pouvait pas être assez souligné!