Comprendre la récursion de mergesort
la plupart des implémentations de mergesort que je vois sont similaires à ceci. introduction aux algorithmes livre avec en ligne implantations je recherche. Mes mouvements de récursion ne vont pas beaucoup plus loin que de jouer avec la génération de Fibonacci (ce qui était assez simple) donc peut-être que c'est les récursions multiples qui me soufflent l'esprit, mais je ne peux même pas passer à travers le code et comprendre ce qui se passe avant même que j'appuie sur la fonction de fusion.
Comment est-il pas à pas dans cette? Est-il une stratégie ou lecture que je devrais subir pour mieux comprendre le processus ici?
void mergesort(int *a, int*b, int low, int high)
{
int pivot;
if(low<high)
{
pivot=(low+high)/2;
mergesort(a,b,low,pivot);
mergesort(a,b,pivot+1,high);
merge(a,b,low,pivot,high);
}
}
et la fusion(bien franchement, je suis mentalement bloqué avant même d'arriver à cette partie)
void merge(int *a, int *b, int low, int pivot, int high)
{
int h,i,j,k;
h=low;
i=low;
j=pivot+1;
while((h<=pivot)&&(j<=high))
{
if(a[h]<=a[j])
{
b[i]=a[h];
h++;
}
else
{
b[i]=a[j];
j++;
}
i++;
}
if(h>pivot)
{
for(k=j; k<=high; k++)
{
b[i]=a[k];
i++;
}
}
else
{
for(k=h; k<=pivot; k++)
{
b[i]=a[k];
i++;
}
}
for(k=low; k<=high; k++) a[k]=b[k];
}
9 réponses
je pense que le nom de la fonction" sort "dans MergeSort est un peu impropre, il devrait vraiment s'appeler"diviser".
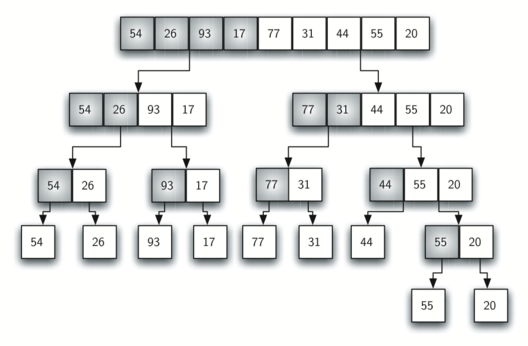
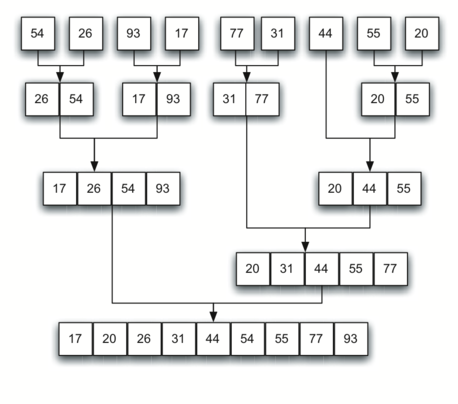
Voici une visualisation de l'algorithme dans le processus.

chaque fois que la fonction réapparaît, elle travaille sur une subdivision de plus en plus petite du tableau d'entrée, en commençant par la moitié gauche de celui-ci. Chaque fois que la fonction revient de la récursion, elle va continuer et soit commencer à travailler sur la moitié droite, ou recommencez et travaillez sur une plus grande moitié.
Comme ceci
[************************]mergesort
[************]mergesort(lo,mid)
[******]mergesort(lo,mid)
[***]mergesort(lo,mid)
[**]mergesort(lo,mid)
[**]mergesort(mid+1,hi)
[***]merge
[***]mergesort(mid+1,hi)
[**]mergesort*(lo,mid)
[**]mergesort(mid+1,hi)
[***]merge
[******]merge
[******]mergesort(mid+1,hi)
[***]mergesort(lo,mid)
[**]mergesort(lo,mid)
[**]mergesort(mid+1,hi)
[***]merge
[***]mergesort(mid+1,hi)
[**]mergesort(lo,mid)
[**]mergesort(mid+1,hi)
[***]merge
[******]merge
[************]merge
[************]mergesort(mid+1,hi)
[******]mergesort(lo,mid)
[***]mergesort(lo,mid)
[**]mergesort(lo,mid)
[**]mergesort(mid+1,hi)
[***]merge
[***]mergesort(mid+1,hi)
[**]mergesort(lo,mid)
[**]mergesort(mid+1,hi)
[***]merge
[******]merge
[******]mergesort(mid+1,hi)
[***]mergesort(lo,mid)
[**]mergesort*(lo,mid)
[**]mergesort(mid+1,hi)
[***]merge
[***]mergesort(mid+1,hi)
[**]mergesort(lo,mid)
[**]mergesort(mid+1,hi)
[***]merge
[******]merge
[************]merge
[************************]merge
FUSION SORT:
1) Diviser le tableau en deux
2) Trier la moitié gauche
3) Trier la moitié droite
4) Fusionner les deux moitiés ensemble
une chose évidente à faire serait d'essayer cette sorte de fusion sur un petit tableau, disons taille 8 (Puissance de 2 est pratique ici), sur papier. Faites comme si vous étiez un ordinateur qui exécute le code, et voyez s'il commence à devenir un peu plus clair.
votre question est un peu ambiguë parce que vous n'expliquez pas ce que vous trouvez confus, mais il semble que vous essayez de dérouler les appels récursifs dans votre tête. Qui peut ou peut ne pas être une bonne chose, mais je pense qu'il peut facilement conduire à avoir trop bien dans votre tête à la fois. Au lieu d'essayer de tracer le code du début à la fin, voyez si vous pouvez comprendre le concept abstraitement. Fusion de tri:
- Divise le tableau en deux
- Trie la moitié gauche
- Trie la moitié droite
- Fusionne les deux moitiés ensemble
(1) devrait être assez évident et intuitif pour vous. Pour l'étape (2) l'idée clé est présent, la moitié gauche d'un tableau... est un tableau. en Supposant que votre fusion tri fonctionne, il doit être capable de classer la moitié gauche du tableau. Droit? Step (4) est en fait une partie assez intuitive de l'algorithme. Un exemple devrait la rendre insignifiante:
at the start
left: [1, 3, 5], right: [2, 4, 6, 7], out: []
after step 1
left: [3, 5], right: [2, 4, 6, 7], out: [1]
after step 2
left: [3, 5], right: [4, 6, 7], out: [1, 2]
after step 3
left: [5], right: [4, 6, 7], out: [1, 2, 3]
after step 4
left: [5], right: [6, 7], out: [1, 2, 3, 4]
after step 5
left: [], right: [6, 7], out: [1, 2, 3, 4, 5]
after step 6
left: [], right: [7], out: [1, 2, 3, 4, 5, 6]
at the end
left: [], right: [], out: [1, 2, 3, 4, 5, 6, 7]
donc en supposant que vous comprenez (1) et (4), une autre façon de penser à une sorte de fusion serait celle-ci. Imaginez quelqu'un d'autre a écrit mergesort() et si vous êtes sûr qu'il fonctionne. Vous pourriez alors utiliser cette implémentation de mergesort() pour écrire:
sort(myArray)
{
leftHalf = myArray.subArray(0, myArray.Length/2);
rightHalf = myArray.subArray(myArray.Length/2 + 1, myArray.Length - 1);
sortedLeftHalf = mergesort(leftHalf);
sortedRightHalf = mergesort(rightHalf);
sortedArray = merge(sortedLeftHalf, sortedRightHalf);
}
Notez que sort ne pas utiliser la récursivité. Ça dit juste "trier les deux moitiés et les fusionner". Si vous avez compris l'exemple de fusion ci-dessus, alors j'espère que vous voyez intuitivement que cela sort la fonction semble faire ce qu'elle dit... sorte.
Maintenant, si vous regardez plus attentivement... sort() regarde à peu près exactement comme mergesort()! C'est parce que c'est mergesort() (sauf qu'il n'a pas de cas de base parce qu'il n'est pas récursif!).
mais c'est comme ça que j'aime penser à récursif fonctions: supposons que la fonction fonctionne, quand vous l'appelez. Traitez-le comme une boîte noire qui fait ce dont vous avez besoin. Lorsque vous effectuez cette hypothèse, à comprendre comment remplir cette boîte noire est souvent facile. Pour une entrée donnée, vous pouvez le décomposer en petites entrées pour nourrir votre boîte noire? Après avoir résolu cela, la seule chose qui reste est de gérer les cas de base au début de votre fonction (qui sont les cas où vous n'avez pas besoin de faire des appels récursifs. Par exemple, mergesort([]) juste renvoie un tableau vide; il ne fait pas d'appel récursif à