Algorithme de l'arbre de suffixe d'Ukkonen en anglais simple
je me sens un peu épaisse à ce point. J'ai passé des jours à essayer de me concentrer sur la construction d'un arbre à suffixe, mais comme je n'ai pas de formation mathématique, beaucoup d'explications m'échappent alors qu'elles commencent à faire un usage excessif de la symbologie mathématique. La plus proche d'une bonne explication que j'ai trouvé est recherche de chaîne rapide avec des arbres de suffixe , mais il glose sur divers points et certains aspects de l'algorithme restent clair.
une explication étape par étape de cet algorithme ici sur le débordement de la pile serait inestimable pour beaucoup d'autres à part moi, je suis sûr.
pour référence, voici le papier D'Ukkonen sur l'algorithme: http://www.cs.helsinki.fi/u/ukkonen/SuffixT1withFigs.pdf
ma compréhension de base, jusqu'à présent:
- je dois itérer à travers chaque préfixe P d'une chaîne donnée T
- je dois itérer à travers chaque suffixe du préfixe P et ajouter cela à l'arbre
- pour ajouter le suffixe S à l'arbre, je dois itérer à travers chaque caractère en S, avec les itérations consistant soit à marcher le long d'une branche existante qui commence avec le même ensemble de caractères C en S et potentiellement diviser un bord en noeuds descendants lorsque j'atteins un caractère différent dans le suffixe, ou s'il n'y avait pas de bord correspondant pour marcher vers le bas. Lorsque l'absence de correspondance edge est trouvé pour marcher vers le bas pour C, un nouveau bord de feuille est créé pour C.
l'algorithme de base semble être O(N 2 ), comme il est souligné dans la plupart des explications, comme nous avons besoin d'étape à travers tous les préfixes, puis nous avons besoin d'étape à travers chacun des suffixes pour chaque préfixe. L'algorithme d'Ukkonen est apparemment unique à cause de la technique de pointeur de suffixe qu'il utilise, bien que je pense que est ce que j'ai des problèmes compréhension.
je suis aussi avoir de la difficulté à comprendre:
- exactement quand et comment le "point actif" est attribué, utilisés et modifiés
- ce qui se passe avec la canonisation aspect de l'algorithme de
- pourquoi les implémentations que j'ai vu ont besoin de "corriger" les variables limitatives qu'ils utilisent
Voici la version complète C# code source. Il ne fonctionne pas seulement correctement, mais prend en charge la canonisation automatique et rend un plus beau graphique de texte de la sortie. Code Source et sortie de l'échantillon:
https://gist.github.com/2373868
mise à jour 2017-11-04
après tant d'années j'ai trouvé une nouvelle utilisation pour les arbres de suffixe, et ont mis en œuvre l'algorithme dans JavaScript . Gist est ci-dessous. Il doit être exempt de bogues. La déverser dans un fichier js, npm install chalk à partir du même emplacement, puis exécutez avec le noeud.js pour voir une sortie colorée. Il y a une version dépouillée dans le même Gist, sans aucun code de débogage.
https://gist.github.com/axefrog/c347bf0f5e0723cbd09b1aaed6ec6fc6
6 réponses
ce qui suit est une tentative de décrire L'algorithme D'Ukkonen en montrant d'abord ce qu'il fait lorsque la chaîne est simple (i.e. ne contient pas de caractères répétés), puis en l'étendant à l'algorithme complet.
tout d'abord, quelques déclarations préliminaires.
-
ce que nous construisons, c'est fondamentalement comme un essai de recherche. Donc il y est un nœud racine, les bords sortant de lui conduisant à de nouveaux noeuds, et d'autres bords sortant de ceux-ci, et ainsi de suite
-
mais : contrairement à un essai de recherche, les étiquettes de bord ne sont pas simples caractère. Au lieu de cela, chaque bord est étiqueté en utilisant une paire d'entiers
[from,to]. Ce sont des indicateurs dans le texte. En ce sens, chaque edge porte une étiquette de chaîne de longueur arbitraire, mais ne prend que O(1) l'espace (deux pointeurs).
principe de base
je voudrais d'abord montrer comment créer le suffixe d'un arbre chaîne particulièrement simple, une chaîne sans caractères répétés:
abc
l'algorithme fonctionne par étapes, de gauche à droite . Il y a un pas pour chaque caractère de la chaîne . Chaque étape peut comporter plus d'une opération individuelle, mais nous le verrons (voir les observations finales à la fin) que le nombre total d'opérations est O(n).
ainsi, nous commençons par le gauche , et insérons d'abord seulement le caractère unique
a en créant un bord à partir du noeud de racine (à gauche) à une feuille,
et l'étiqueter comme [0,#] , ce qui signifie que le bord représente le
sous-couche commençant à la position 0 et se terminant à l'extrémité du courant . Je
l'utilisation du symbole # pour signifier l'extrémité actuelle , qui est à la position 1
(juste après a ).
nous avons donc un arbre initial, qui ressemble à ceci:
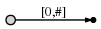
et ce qu'il signifie Est ceci:
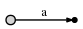
maintenant nous progressons à la position 2 (juste après b ). notre objectif à chaque étape
est d'insérer tous les suffixes jusqu'à la position actuelle . Nous faisons cela
par
- extension de l'actuel
a- bord àab - insérant un nouveau bord pour
b
dans notre représentation cela ressemble à
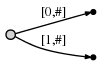
Et ce que cela signifie est:
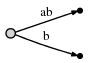
nous observons deux choses:
- la représentation de bord pour
abest la même qu'elle était dans l'arbre initial:[0,#]. Sa signification a automatiquement changé parce que nous avons mis à jour la position actuelle#de 1 à 2. - chaque bord consomme O (1) espace, parce qu'il se compose de seulement deux les pointeurs dans le texte, quel que soit le nombre de caractères représenter.
ensuite, nous incrémentons de nouveau la position et mettre à jour l'arbre en ajoutant
un c à chaque bord existant et insérant un nouveau bord pour le nouveau
le suffixe c .
dans notre représentation cela ressemble à
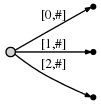
et ce qu'il
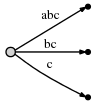
nous observons:
- L'arbre est le bon suffixe arbre jusqu'à la position actuelle après chaque étape
- Il y a autant d'étapes qu'il y a de caractères dans le texte
- la quantité de travail dans chaque étape est O (1), parce que tous les bords existants
être mise à jour automatique en incrémentant
#, et en insérant le un nouveau bord pour le caractère final peut être fait en O(1) temps. Par conséquent, pour une chaîne de longueur n, seul le temps O(n) est requis.
première extension: répétitions simples
bien sûr, cela fonctionne si bien seulement parce que notre corde ne contenir les répétitions. Nous regardons maintenant une chaîne de caractères plus réaliste:
abcabxabcd
ça commence avec abc comme dans l'exemple précédent, puis ab est répété
et suivi de x , puis abc est répété suivi de d .
les Étapes 1 à 3: Après les 3 premières étapes, nous avons l'arbre de l'exemple précédent:
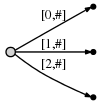
Étape 4: Nous allons # à la position 4. Ce met implicitement à jour tous les
bords à ceci:
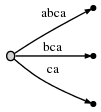
et nous avons besoin d'insérer le suffixe final de l'étape actuelle, a , à
racine.
avant de faire ceci, nous introduisons deux autres variables (en plus de
# ), ce qui bien sûr ont été là tout le temps, mais nous n'avons pas utilisé
jusqu'à présent:
- Le point actif , qui est un triple
(active_node,active_edge,active_length) - le
remainder, qui est un entier indiquant combien de nouveaux suffixes nous devons insérer
la signification exacte de ces deux sera bientôt claire, mais pour l'instant disons simplement:
- dans l'exemple simple
abc, le point actif était toujours(root,'"1519280920"x',0), i.e.active_nodeétait le noeud racine,active_edgea été spécifié comme le caractère nul'" 1519310920"x', etactive_lengthétait zéro. L'effet de ceci était que le seul nouveau bord qui nous avons inséré dans chaque étape a été inséré au noeud racine comme un fraîchement créé bord. Nous verrons bientôt pourquoi un triple est nécessaire pour représentez cette information. - le
remaindera toujours été mis à 1 au début de chaque étape. La signification de ceci était que le nombre de suffixes que nous avions à activement insérer à la fin de chaque l'étape a été de 1 (toujours à la caractère final).
Maintenant, cela va changer. Lorsque nous insérons le courant final
caractère a à la racine, on remarque qu'il y a déjà une sortie
bord commençant par a , spécifiquement: abca . Voici ce que nous faisons dans
un tel cas:
- Nous ne pas insérer une nouvelle edge
[4,#]au nœud racine. Au lieu de cela nous simplement avis que le suffixeaest déjà dans notre arbre. Il se termine au milieu d'un bord plus long, mais nous ne sommes pas gêné par cela. Nous venons juste de laisser les choses comme elles sont. - Nous définir le point actif à
(root,'a',1). Cela signifie que l'actif point est maintenant quelque part au milieu du bord sortant du noeud racine qui commence para, spécifiquement, après la position 1 sur ce bord. Nous notez que le bord est spécifié par sa simple premier le caractèrea. Cela suffit car il peut y avoir un seul bord en commençant par n'importe quel caractère particulier (confirmer que c'est vrai après avoir lu toute la description). - nous incrémentons aussi
remainder, donc au début de l'étape suivante il sera de 2.
Observation: lorsque le suffixe final que nous devons insérer se trouve à
exister dans l'arbre déjà , l'arbre lui-même est pas changé du tout (nous ne mettons à jour le point actif et remainder ). Arbre
n'est donc pas une représentation précise de l'arbre de suffixe jusqu'au
position actuelle plus, mais il contient tous les suffixes (parce que le final
le suffixe a est contenu implicitement ). Ainsi, en dehors de la mise à jour de la
variables (qui sont tous de longueur fixe, c'est donc O(1)), il y avait
pas de travail fait à cette étape.
Étape 5: Nous avons mise à jour de la position actuelle # à 5. Ce
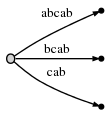
et parce que remainder est 2 , nous avons besoin d'insérer deux final
suffixes de la position actuelle: ab et b . C'est essentiellement parce que:
- le suffixe
ade l'étape précédente n'a jamais été correctement insérer. Ainsi, est resté , et puisque nous avons progressé un step, il est passé deaàab. - et nous devons insérer le nouveau bord final
b.
Dans la pratique, cela signifie que nous allons à le point actif (qui indique
derrière le a sur ce qui est maintenant le abcab bord), et insérer le
caractère final actuel b . mais: encore une fois, il s'avère que b est
déjà présent sur le même bord.
Donc, encore une fois, nous ne changeons pas l'arbre. Tout simplement:
- mettre à Jour le point actif
(root,'a',2)(même nœud et le bord comme avant, mais maintenant nous pointons à l'arrière theb) - augmente le
remainderà 3 parce que nous n'avons toujours pas correctement inséré l'arête finale de l'étape précédente, et nous ne l'insérez pas le courant de l'arête finale.
Pour être clair: Nous avons dû insérer ab et b dans l'étape actuelle, mais
comme ab a déjà été trouvé, nous avons mis à jour le point actif et
n'essayez même pas d'insérer b . Pourquoi? Parce que si ab est dans l'arbre,
chaque suffixe (y compris b ) doit être dans l'arbre,
trop. Peut-être seulement implicitement , mais il doit être là, en raison de la
façon dont nous avons construit l'arbre jusqu'à présent.
nous procédons à étape 6 en incrémentant # . L'arbre est
mise à jour automatique:
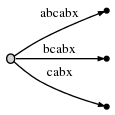
parce que remainder est 3 , nous devons insérer abx , bx et
x . Le point actif nous dit Où se termine ab , donc nous n'avons qu'à
sauter là et insérez le x . En effet, x n'est pas encore là, donc nous
fendre le bord abcabx et insérer un noeud interne:
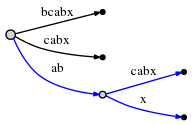
les représentations de bord sont toujours des pointeurs dans le texte, si le fractionnement et l'insertion d'un noeud interne peut être fait en O(1) fois.
nous avons donc traité de abx et du Décret remainder à 2. Maintenant, nous
besoin d'insérer le prochain suffixe restant, bx . Mais avant de faire ça
nous devons mettre à jour le point actif. La règle pour cela, après séparation
et en insérant un bord, sera appelé Règle 1 ci-dessous, et il s'applique chaque fois que le
active_node est racine (nous apprendrons la règle 3 pour les autres cas
dessous.) Voici la règle 1:
après une insertion à partir de la racine,
active_nodereste racineactive_edgeest placé au premier caractère du nouveau suffixe we besoin d'insérer, c'est à direbactive_lengthest réduit de 1
D'où, le nouveau point actif triple (root,'b',1) indique que le
l'insertion suivante doit être faite au bord bcabx , derrière 1 caractère,
c'est à dire derrière b . Nous pouvons identifier le point d'insertion dans le temps O (1) et
vérifiez si x est déjà présent ou non. Si elle était présente, nous
finirait l'étape actuelle et laisserait tout comme il est. Mais x
n'est pas présent, nous l'insérons donc en fendant le bord:
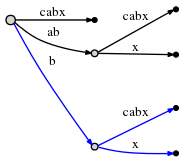
Encore une fois, cela a pris O (1) temps et nous mettons à jour remainder à 1 et le
point actif (root,'x',0) comme la règle 1 des états.
Mais il y a une chose que nous devons faire. Nous l'appellerons règle 2:
si nous divisons un bord et insérons un nouveau noeud, et si c'est pas le premier noeud créé pendant l'étape en cours, nous connectons le précédent inséré nœud et le nœud par un pointeur spécial, un suffixe le lien . Nous verrons plus tard pourquoi cela est utile. Voici ce que nous obtenons, le suffixe link est représenté comme un bord pointillé:
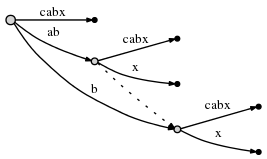
Nous avons encore besoin d'insérer le suffixe final de l'étape en cours,
x . Depuis la composante active_length du noeud actif est tombé
à 0, l'insertion finale se fait directement à la racine. Depuis il n'y a pas de
bord sortant au noeud racine à partir de x , nous insérons un nouveau
bord:
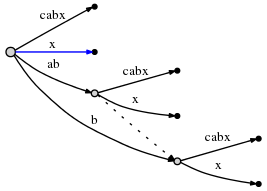
comme nous pouvons le voir, dans l'étape actuelle tous les inserts restants ont été faites.
nous procédons à étape 7 en positionnant # =7, ce qui ajoute automatiquement le caractère suivant,
a , de tous les bords des feuilles, comme toujours. Ensuite, nous essayons d'insérer la nouvelle final
caractère au point actif (la racine), et trouver qu'il est là
déjà. Donc nous terminons l'étape actuelle sans rien insérer et
mettre à jour le point actif à (root,'a',1) .
Dans étape 8 , # =8, nous append b , et comme on l'a vu, cela ne
signifie que nous mettons à jour le point actif à (root,'a',2) et incrément remainder sans faire
autre chose, parce que b est déjà présent. Cependant, nous remarquons(en O (1) temps) que le point actif
est maintenant à la fin d'un bord. Nous le reflétons en le rétablissant pour
(node1,'"15191010920"x',0) . Ici, j'utilise node1 pour faire référence à
noeud interne le bord ab se termine à.
ensuite, dans étape # =9 , nous devons insérer "c" et cela nous aidera à
comprendre la dernière astuce:
Deuxième extension: à l'Aide du suffixe liens
comme toujours, la mise à jour # ajoute automatiquement c aux bords des feuilles
et nous allons le point actif pour voir si nous pouvons insérer un "c". Il tourne
"c' existe déjà à bord, donc nous avons mis le point actif à
(node1,'c',1) , incrémenter remainder et ne rien faire d'autre.
maintenant dans étape # =10 , remainder is 4 , et donc nous devons d'abord insérer
abcd (qui reste d'il y a 3 étapes) par insérant d à l'active
point.
tenter d'insérer d au point actif provoque une fissure du bord
O(1) heure:
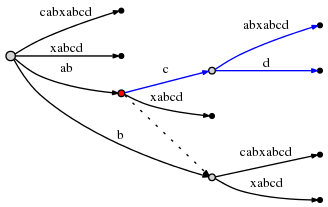
le active_node , à partir duquel la séparation a été amorcée, est marqué en
rouge ci-dessus. Voici la règle finale, Règle 3:
après avoir fendu un bord d'un
active_nodece n'est pas la racine noeud, nous suivons le lien de suffixe sortant de ce noeud, s'il y a tout, et réinitialiser leactive_nodeau noeud qu'il pointe. Si il y a pas de lien de suffixe, nous définissons leactive_nodeà la racine.active_edgeetactive_lengthreste inchangé.
donc le point actif est maintenant (node2,'c',1) , et node2 est marqué en
rouge ci-dessous:
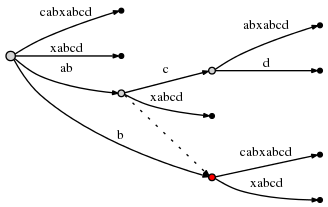
puisque l'insertion de abcd est complète, nous décrétons remainder à
3 et considérer le prochain suffixe restant de l'étape actuelle,
bcd . La règle 3 a placé le point actif juste au bon noeud et au bon bord
ainsi l'insertion de bcd peut être faite simplement en insérant son caractère final
d au point actif.
faisant cela provoque une autre fissure de bord, et en raison de la règle 2 , nous devez créer un lien de suffixe du noeud précédemment inséré vers le nouveau l'un:
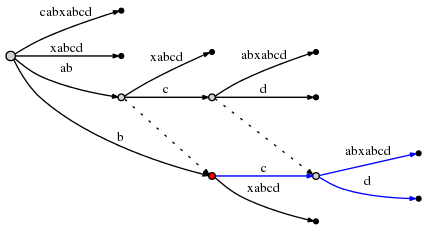
nous observons: les liens de suffixe nous permettent de réinitialiser le point actif afin que nous
peut faire le prochain restant insérer à O (1) effort. Regardez le
graphique ci-dessus pour confirmer qu'effectivement le noeud à l'étiquette ab est lié à
le noeud à b (son suffixe), et le noeud à abc est liée à
bc .
L'étape actuelle n'est pas encore terminée. remainder est maintenant 2, et nous
il faut suivre la règle 3 pour réinitialiser le point actif. Depuis le
courant active_node (rouge ci-dessus) n'a pas de lien de suffixe, nous réinitialisons
racine. Le point actif est maintenant (root,'c',1) .
D'où la prochaine insertion se produit au bord sortant du noeud racine
dont l'étiquette commence par c : cabxabcd , derrière la première caractère,
c'est à dire derrière c . Cela provoque une autre scission:
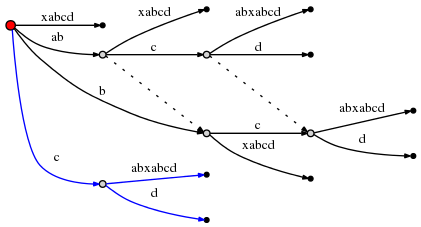
Et depuis cela implique la création d'un nouveau noeud interne,nous suivons règle 2 et définir un nouveau lien de suffixe à partir du précédent créé interne node:
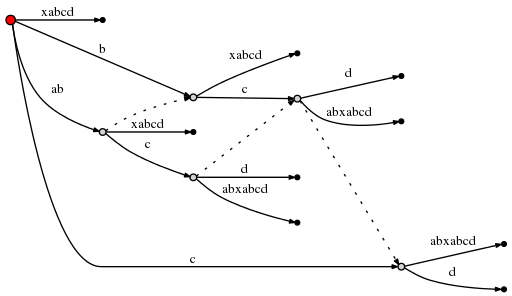
(j'utilise Graphviz Dot pour ces petits graphique. Le nouveau lien de suffixe causé point de réorganiser l'existant les bords, donc vérifiez soigneusement pour confirmer que la seule chose qui était inséré ci-dessus est un nouveau suffixe lien.)
avec ceci, remainder peut être réglé à 1 et puisque le active_node est
root, nous utilisons la règle 1 pour mettre à jour le point actif en (root,'d',0) . Ce
signifie que l'insertion finale de l'étape actuelle est d'insérer un seul d
à la racine:
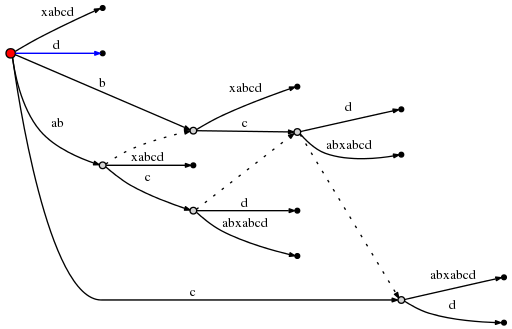
C'était la dernière étape et nous sommes faits. Il y a le nombre de final observations , cependant:
-
à chaque pas nous avançons
#d'une position. Cela automatiquement les mises à jour de tous les nœuds feuilles en O(1) fois. -
mais il ne traite pas a) des suffixes restants de la précédente les étapes, et b) à la dernière caractère de l'étape en cours.
-
remainder" nous dit combien d'inserts supplémentaires nous avons besoin pour faire. Ces inserts correspondent à un à un aux derniers suffixes de la chaîne qui se termine à la position actuelle#. Nous en considérons un après les autres et de faire l'insertion. Important: chaque insertion est fait en O(1) fois depuis le point actif nous dit exactement où aller, et nous devons ajouter qu'un seul personnage à l'actif des point. Pourquoi? Parce que les autres caractères sont contenus implicitement (sinon, le point actif ne serait pas où il est). -
après chacun de ces mots, nous décrétons
remainderet suffixe lien si il y en a. Si nous pas à la racine (règle 3). Si nous sont déjà à la racine, nous modifions le point actif en utilisant la règle 1. Dans dans tous les cas, cela ne prend que du temps O(1). -
si, au cours de l'une de ces insertions, nous trouvons que le personnage que nous voulons pour insérer est déjà là, nous ne faisons rien et pas actuel, même si
remainder>0. La raison en est que toute les inserts qui restent seront des suffixes de celui que nous venons d'essayer de faire. Par conséquent, ils sont tous implicite dans l'arborescence actuelle. Fait queremainder> 0 s'assure que nous traitons avec les suffixes restants tard. -
et si à la fin de l'algorithme
remainder>0? Ce sera le cas où la fin du texte est un substrat qui s'est produit quelque part avant. Dans ce cas, nous devons ajouter un caractère supplémentaire à la fin de la chaîne qui n'a pas eu lieu avant. Dans le la littérature, habituellement le signe de dollar$est utilisé comme un symbole pour que. quelle importance? -- > si plus tard nous utilisons l'arbre des suffixes complété pour rechercher des suffixes, nous doit accepter les allumettes seulement si elles se terminent à une feuille . Sinon nous obtiendrions beaucoup de fausses correspondances, parce qu'il y a beaucoup cordes implicitement contenues dans l'arbre qui ne sont pas des suffixes réels de la chaîne principale. Forçantremainderà 0 à la fin est essentiellement un moyen de s'assurer que tous les suffixes fin à un nœud feuille. cependant, si nous voulons utiliser l'arbre pour rechercher général sous-chaînes , pas seulement suffixes de la chaîne principale, cette dernière étape est en fait pas nécessaire, comme le suggère le cas des OP commentaire ci-dessous. -
alors quelle est la complexité de l'algorithme entier? Si le texte est n les caractères en longueur, il y a évidemment n pas (ou n+1 si on ajoute le signe du dollar). A chaque étape, soit nous ne faisons rien (autre que mise à jour des variables), ou nous faisons
remainderinsertions, chaque prise O (1) temps. Depuisremainderindique combien de fois nous n'avons rien fait dans les étapes précédentes, et est décrémenté à chaque insertion que nous faisons maintenant, le nombre total de fois que nous faisons quelque chose est exactement n (ou n+1). Par conséquent, la complexité totale est O(n). -
cependant, il y a une petite chose que je n'ai pas correctement expliqué: Il peut arriver que nous suivions un lien de suffixe, point, et puis trouver que son composant
active_lengthne travaillez bien avec le nouveauactive_node. Par exemple, envisagez une situation comme ceci:
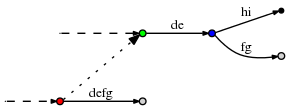
(les lignes pointillées indiquent le reste de l'arbre. La ligne pointillée est une suffixe lien.)
maintenant, que le point actif soit (red,'d',3) , donc il pointe à la place
derrière le f sur le defg bord de. Maintenant supposons que nous ayons fait le nécessaire
mise à jour et maintenant suivez le lien du suffixe pour mettre à jour le point actif
conformément à l'article 3. Le nouveau point actif est (green,'d',3) . Cependant,
le d - bord sortant du noeud vert est de , donc il n'a que 2
caractère. Afin de trouver le point actif correct, nous
besoin de suivre ce bord au noeud bleu et de réinitialiser à (blue,'f',1) .
dans un cas particulièrement grave, le active_length pourrait être aussi grand que
remainder , qui peut être aussi grand que n. Et il pourrait très bien arriver
que pour trouver le point actif correct, il ne suffit pas de sauter par-dessus un
noeud interne, mais peut-être beaucoup, jusqu'à n dans le pire des cas. Ne que
moyenne l'algorithme a une complexité cachée O(N 2 ), parce que
dans chaque étape remainder est généralement O (n), et les post-ajustements
au noeud actif après avoir suivi un lien de suffixe pourrait être O (n), aussi?
Pas de. La raison en est que si en effet, nous devons ajuster le point actif
(par exemple de vert à bleu comme ci-dessus), qui nous amène à un nouveau noeud qui
possède son propre suffixe, et active_length sera réduit. Comme
nous suivons la chaîne des liens de suffixe nous faisons les inserts restants, active_length ne peut que
et le nombre d'ajustements de points actifs que nous pouvons faire sur
le chemin ne peut pas être plus grand que active_length à un moment donné. Depuis
active_length ne peut jamais être plus grand que remainder , et remainder
est O(n) pas seulement à chaque étape, mais la somme totale des incréments
jamais fait de remainder au cours de l'ensemble du processus est
O (n) aussi, le nombre d'ajustements de points actifs est limité par
O (n).
j'ai essayé de mettre en œuvre l'Arbre de Suffixe avec l'approche donnée dans la réponse de jogojapan, mais cela n'a pas fonctionné pour certains cas en raison de la formulation utilisée pour les règles. De plus, j'ai mentionné que personne n'a réussi à implémenter un arbre de suffixe absolument correct en utilisant cette approche. Ci-dessous, je vais écrire un "aperçu" de la réponse de jogojapan avec quelques modifications aux règles. Je vais également décrire le cas lorsque nous oublions de créer important suffixe des liens.
variables supplémentaires utilisées
- active point - un triple (active_node; active_edge; active_length), montrant d'où nous devons commencer à insérer un nouveau suffixe.
- reste - indique le nombre de suffixes que nous devons ajouter explicitement . Par exemple, si notre mot est "abcaabca", et reste = 3, cela signifie que nous devons processus 3 derniers suffixes: bca , ca et un .
utilisons le concept d'un noeud interne - tous les noeuds, sauf le racine et le leafs sont noeuds internes .
Observation 1
lorsque le suffixe final que nous devons insérer se trouve déjà exister dans l'arbre, l'arbre lui-même n'est pas changé du tout (nous ne mettons à jour que les active point et remainder ).
Observation 2
si, à un moment donné, active_length est supérieur ou égal à la longueur du bord actuel ( edge_length ), nous déplaçons notre active point vers le bas jusqu'à ce que edge_length soit strictement supérieur à active_length .
maintenant, redéfinissons les règles:
Règle 1
si après une insertion à partir du noeud actif = root , la longueur active est supérieure à 0, alors:
- nœud actif n'est pas modifiée
- longueur active est décrémenté
- Active edge est décalé à droite (au premier caractère du suffixe suivant il faut insérer)
règle 2
Si nous créons un nouveau noeud interne OU faire une insertion d'un noeud interne , et ce n'est pas le d'abord tel noeud interne à l'étape actuelle, puis nous relions le précédent tel noeud avec ce un à travers un lien suffixe .
cette définition du Rule 2 est différente de jogojapan', car ici nous prenons en compte non seulement le nouvellement créé noeuds internes, mais aussi les noeuds internes, à partir de laquelle nous faire une insertion.
Règle 3
après un insert du noeud actif qui n'est pas le root noeud, nous devons suivre le lien de suffixe et mettre le noeud actif au noeud qu'il pointe. S'il n'y a pas de lien de suffixe, définissez le noeud actif au noeud racine . De toute façon, active bord et longueur restent inchangées.
dans cette définition de Rule 3 nous considérons également les inserts de noeuds foliaires (pas seulement Split-nodes).
et enfin, Observation 3:
lorsque le symbole que nous voulons ajouter à l'arbre est déjà sur le bord, nous , selon Observation 1 , mettre à jour seulement active point et remainder , laissant l'arbre inchangé. mais s'il y a un noeud interne marqué comme ayant besoin d'une liaison de suffixe , nous devons connecter ce noeud avec notre active node actuel par une liaison de suffixe.
regardons l'exemple d'un arbre de suffixe pour cdddcdc si nous ajoutons un lien de suffixe dans un tel cas et si nous ne le faisons pas:
-
Si nous NE PAS connecter les nœuds grâce à un suffixe lien:
- avant d'ajouter la dernière lettre c :
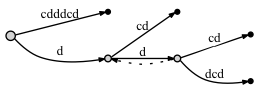
- après l'ajout de la dernière lettre c :
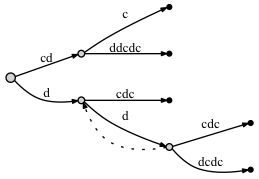
-
Si nous FAIRE connecter les nœuds grâce à un suffixe lien:
- avant d'ajouter la dernière lettre c :
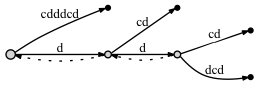
- après l'ajout de la dernière lettre c :
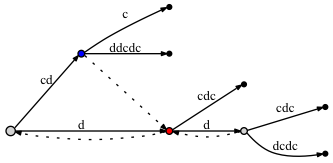
semble comme il n'y a pas de différence significative: dans le deuxième cas il y a deux liens de suffixe supplémentaires. Mais ces liens de suffixe sont correct , et l'un d'eux - du noeud bleu au noeud rouge - est très important pour notre approche avec point actif . Le problème est que si nous ne mettons pas de lien de suffixe ici, plus tard, quand nous ajoutons de nouvelles lettres à l'arbre, nous pourrions omettre d'ajouter des noeuds à l'arbre en raison de le Rule 3 , parce que, selon lui, s'il n'y a pas de lien de suffixe, alors nous devons mettre le active_node à la racine.
lorsque nous avons ajouté la dernière lettre à l'arbre, le noeud rouge avait déjà existé avant que nous avons fait un insert à partir du noeud bleu (le bord a câblé 'c' ). Comme il y avait un insert du noeud bleu, nous le marquons comme nécessitant un lien de suffixe . Puis, en s'appuyant sur la point actif approche, le active node a été placé sur le nœud rouge. Mais nous ne faisons pas un insert à partir du noeud rouge, comme la lettre 'c' est déjà sur le bord. Signifie que le noeud bleu doit être laissé sans un suffixe lien? Non, nous devons connecter le noeud bleu avec le noeud rouge à travers un lien de suffixe. Pourquoi est-il correct? Parce que l'approche point actif garantit que nous arrivons à un bon endroit, i.e., à la place suivante où nous devons traiter un insert d'un suffixe plus court .
enfin, voici mes implémentations de L'Arbre de suffixe:
espère que cette" vue d'ensemble " combinée avec la réponse détaillée de jogojapan aidera quelqu'un à mettre en œuvre son propre arbre de suffixe.
Merci pour le tutoriel bien expliqué par @jogojapan , j'ai implémenté l'algorithme en Python.
quelques problèmes mineurs mentionnés par @jogojapan s'avèrent être plus sophistiqué que je ne m'y attendais, et doivent être traités avec beaucoup de soin. Il m'a fallu plusieurs jours pour obtenir mon implémentation assez robuste (je suppose). Les problèmes et les solutions sont énumérés ci-dessous:
-
fin avec
Remainder > 0il s'avère que cette situation peut également se produire pendant l'étape de déploiement , pas seulement la fin de l'algorithme entier. Lorsque cela se produit, nous pouvons laisser le reste, actnode, actedge, et actlength inchangé , mettre fin à l'étape de déploiement en cours, et commencer une autre étape en continuant à se plier ou à se déployer en fonction de si le prochain char dans la chaîne d'origine est sur le chemin d'accès actuel ou pas. -
sautez au-dessus des Noeuds: lorsque nous suivons un lien de suffixe, mettez à jour le point actif, puis découvrez que son composant active_length ne fonctionne pas bien avec le nouveau code active_node. Nous devons aller de l'avant au bon endroit pour fendre, ou insérer une feuille. Ce processus pourrait être pas si simple parce que pendant le déplacement l'actlength et actedge garder en changeant tout le chemin, quand vous devez revenir au noeud de racine , le actedge et actlength pourrait être faux en raison de ces mouvements. Nous avons besoin de variables supplémentaires pour conserver cette information.
les deux autres problèmes ont été soulignés par @managonov
-
Split pourrait dégénérer en essayant de diviser un bord, parfois vous trouverez l'opération de split est juste sur un noeud. Dans ce cas, nous avons seulement besoin d'ajouter une nouvelle feuille à ce noeud, prenez-le comme une opération standard edge split, ce qui signifie que les liens de suffixe s'il y en a, doivent être maintenus en conséquence.
-
Liens De Suffixe Cachés il y a un autre cas particulier qui est encouru par problème 1 et problème 2 . Parfois nous avons besoin de sauter sur plusieurs noeuds au bon point pour split, nous pourrions surpasser le bon point si nous nous déplaçons en comparant la chaîne du reste et les étiquettes de chemin. Dans ce cas, la liaison de suffixe sera négligée involontairement, s'il y en a une. Cela pourrait être évité en en se rappelant le bon point en avançant. Le lien de suffixe doit être maintenu si le noeud divisé existe déjà, ou même le problème 1 se produit pendant une étape de déploiement.
enfin, mon implémentation dans Python est la suivante:
Conseils: il comprend une naïve impression arborescente fonction dans le code ci-dessus, qui est très important lors du débogage . Il m'a sauvé beaucoup de temps et est commode pour localiser des cas spéciaux.
mon intuition est la suivante:
Après k itérations de la boucle principale, vous avez construit un suffixe arbre qui contient tous les suffixes de la chaîne complète qui commencent dans les k premiers caractères.
au début, cela signifie que l'arbre de suffixe contient un seul noeud racine qui représente la chaîne entière (c'est le seul suffixe qui commence à 0).
après les itérations Len (string) vous avez un arbre de suffixe qui contient tous les suffixes.
pendant la boucle la clé est le point actif. À mon avis, cela représente le point le plus profond de l'arbre des suffixe qui correspond à un suffixe correct des premiers caractères k de la chaîne. (Je pense qu'être correct signifie que le suffixe ne peut pas être la chaîne entière.)
par exemple, supposons que vous ayez vu les caractères 'abcabc'. Le point actif représentent le point de l'arbre correspondant au suffixe "abc".
Le point actif est représenté par (origine,premier,dernier). Cela signifie que vous êtes actuellement au point dans l'arbre où vous arrivez en commençant à l'origine du noeud et puis en vous alimentant dans les caractères dans la chaîne [premier: dernier]
quand vous ajoutez un nouveau caractère, vous regardez pour voir si le point actif est toujours dans l'arbre existant. Si c'est pour que vous vous êtes fait. Sinon, vous devez ajouter un nouveau noeud à l'arbre de suffixe au point actif, repli à la prochaine correspondance la plus courte, et vérifier de nouveau.
Note 1: Les pointeurs de suffixe donnent un lien vers la correspondance la plus courte suivante pour chaque noeud.
Note 2: Lorsque vous ajoutez un nouveau nœud et de secours vous ajoutez un nouveau suffixe pointeur pour le nouveau nœud. La destination de ce pointeur de suffixe sera le noeud au point actif raccourci. Ce noeud existera déjà, ou sera créé lors de la prochaine itération de cette boucle de repli.
Note 3: la partie de canonisation sauve simplement il est temps de vérifier le point actif. Par exemple, supposons que vous utilisiez toujours origin=0, et que vous changiez juste le premier et le dernier. Pour vérifier le point actif, vous devez suivre l'arbre de suffixe à chaque fois le long de tous les noeuds intermédiaires. Il est logique de mettre en cache le résultat de suivre ce chemin en n'enregistrant que la distance du dernier noeud.
pouvez-vous donner un exemple de code de ce que vous entendez par" corriger " les variables limitatives?
mise en garde: j'ai aussi trouvé ceci algorithme particulièrement difficile à comprendre merci donc de réaliser que cette intuition est susceptible d'être incorrecte dans tous les détails importants...
Salut j'ai essayé de mettre en œuvre l'implémentation expliquée ci-dessus dans ruby , s'il vous plaît vérifier. il semble bien fonctionner.
la seule différence dans l'implémentation est que , j'ai essayé d'utiliser l'objet edge au lieu de simplement utiliser des symboles.
il est aussi présent au 151960920" https://gist.github.com/suchitpuri/9304856
require 'pry'
class Edge
attr_accessor :data , :edges , :suffix_link
def initialize data
@data = data
@edges = []
@suffix_link = nil
end
def find_edge element
self.edges.each do |edge|
return edge if edge.data.start_with? element
end
return nil
end
end
class SuffixTrees
attr_accessor :root , :active_point , :remainder , :pending_prefixes , :last_split_edge , :remainder
def initialize
@root = Edge.new nil
@active_point = { active_node: @root , active_edge: nil , active_length: 0}
@remainder = 0
@pending_prefixes = []
@last_split_edge = nil
@remainder = 1
end
def build string
string.split("").each_with_index do |element , index|
add_to_edges @root , element
update_pending_prefix element
add_pending_elements_to_tree element
active_length = @active_point[:active_length]
# if(@active_point[:active_edge] && @active_point[:active_edge].data && @active_point[:active_edge].data[0..active_length-1] == @active_point[:active_edge].data[active_length..@active_point[:active_edge].data.length-1])
# @active_point[:active_edge].data = @active_point[:active_edge].data[0..active_length-1]
# @active_point[:active_edge].edges << Edge.new(@active_point[:active_edge].data)
# end
if(@active_point[:active_edge] && @active_point[:active_edge].data && @active_point[:active_edge].data.length == @active_point[:active_length] )
@active_point[:active_node] = @active_point[:active_edge]
@active_point[:active_edge] = @active_point[:active_node].find_edge(element[0])
@active_point[:active_length] = 0
end
end
end
def add_pending_elements_to_tree element
to_be_deleted = []
update_active_length = false
# binding.pry
if( @active_point[:active_node].find_edge(element[0]) != nil)
@active_point[:active_length] = @active_point[:active_length] + 1
@active_point[:active_edge] = @active_point[:active_node].find_edge(element[0]) if @active_point[:active_edge] == nil
@remainder = @remainder + 1
return
end
@pending_prefixes.each_with_index do |pending_prefix , index|
# binding.pry
if @active_point[:active_edge] == nil and @active_point[:active_node].find_edge(element[0]) == nil
@active_point[:active_node].edges << Edge.new(element)
else
@active_point[:active_edge] = node.find_edge(element[0]) if @active_point[:active_edge] == nil
data = @active_point[:active_edge].data
data = data.split("")
location = @active_point[:active_length]
# binding.pry
if(data[0..location].join == pending_prefix or @active_point[:active_node].find_edge(element) != nil )
else #tree split
split_edge data , index , element
end
end
end
end
def update_pending_prefix element
if @active_point[:active_edge] == nil
@pending_prefixes = [element]
return
end
@pending_prefixes = []
length = @active_point[:active_edge].data.length
data = @active_point[:active_edge].data
@remainder.times do |ctr|
@pending_prefixes << data[-(ctr+1)..data.length-1]
end
@pending_prefixes.reverse!
end
def split_edge data , index , element
location = @active_point[:active_length]
old_edges = []
internal_node = (@active_point[:active_edge].edges != nil)
if (internal_node)
old_edges = @active_point[:active_edge].edges
@active_point[:active_edge].edges = []
end
@active_point[:active_edge].data = data[0..location-1].join
@active_point[:active_edge].edges << Edge.new(data[location..data.size].join)
if internal_node
@active_point[:active_edge].edges << Edge.new(element)
else
@active_point[:active_edge].edges << Edge.new(data.last)
end
if internal_node
@active_point[:active_edge].edges[0].edges = old_edges
end
#setup the suffix link
if @last_split_edge != nil and @last_split_edge.data.end_with?@active_point[:active_edge].data
@last_split_edge.suffix_link = @active_point[:active_edge]
end
@last_split_edge = @active_point[:active_edge]
update_active_point index
end
def update_active_point index
if(@active_point[:active_node] == @root)
@active_point[:active_length] = @active_point[:active_length] - 1
@remainder = @remainder - 1
@active_point[:active_edge] = @active_point[:active_node].find_edge(@pending_prefixes.first[index+1])
else
if @active_point[:active_node].suffix_link != nil
@active_point[:active_node] = @active_point[:active_node].suffix_link
else
@active_point[:active_node] = @root
end
@active_point[:active_edge] = @active_point[:active_node].find_edge(@active_point[:active_edge].data[0])
@remainder = @remainder - 1
end
end
def add_to_edges root , element
return if root == nil
root.data = root.data + element if(root.data and root.edges.size == 0)
root.edges.each do |edge|
add_to_edges edge , element
end
end
end
suffix_tree = SuffixTrees.new
suffix_tree.build("abcabxabcd")
binding.pry
@jogojapan vous avez apporté des explications impressionnantes et la visualisation. Mais comme @makagonov mentionné il manque quelques règles concernant le suffixe de liens. Il est visible de manière agréable en allant pas à pas sur http://brenden.github.io/ukkonen-animation / par le mot "aabaaabb". Lorsque vous passez de l'étape 10 à l'étape 11, Il n'y a pas de lien de suffixe du noeud 5 au noeud 2 mais le point actif se déplace soudainement là.
@makagonov depuis que je vis à Java world I j'ai aussi essayé de suivre votre implémentation pour saisir le flux de travail du bâtiment ST, mais c'était difficile pour moi à cause de:
- combinaison d'arêtes et de noeuds
- utilisant des pointeurs d'index au lieu de références
- pauses consolidés;
- suite déclarations;
donc j'ai fini avec une telle implémentation en Java qui, je l'espère, reflète toutes les étapes d'une manière plus claire et permettra de réduire le temps d'apprentissage pour les autres habitants de Java:
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
public class ST {
public class Node {
private final int id;
private final Map<Character, Edge> edges;
private Node slink;
public Node(final int id) {
this.id = id;
this.edges = new HashMap<>();
}
public void setSlink(final Node slink) {
this.slink = slink;
}
public Map<Character, Edge> getEdges() {
return this.edges;
}
public Node getSlink() {
return this.slink;
}
public String toString(final String word) {
return new StringBuilder()
.append("{")
.append("\"id\"")
.append(":")
.append(this.id)
.append(",")
.append("\"slink\"")
.append(":")
.append(this.slink != null ? this.slink.id : null)
.append(",")
.append("\"edges\"")
.append(":")
.append(edgesToString(word))
.append("}")
.toString();
}
private StringBuilder edgesToString(final String word) {
final StringBuilder edgesStringBuilder = new StringBuilder();
edgesStringBuilder.append("{");
for(final Map.Entry<Character, Edge> entry : this.edges.entrySet()) {
edgesStringBuilder.append("\"")
.append(entry.getKey())
.append("\"")
.append(":")
.append(entry.getValue().toString(word))
.append(",");
}
if(!this.edges.isEmpty()) {
edgesStringBuilder.deleteCharAt(edgesStringBuilder.length() - 1);
}
edgesStringBuilder.append("}");
return edgesStringBuilder;
}
public boolean contains(final String word, final String suffix) {
return !suffix.isEmpty()
&& this.edges.containsKey(suffix.charAt(0))
&& this.edges.get(suffix.charAt(0)).contains(word, suffix);
}
}
public class Edge {
private final int from;
private final int to;
private final Node next;
public Edge(final int from, final int to, final Node next) {
this.from = from;
this.to = to;
this.next = next;
}
public int getFrom() {
return this.from;
}
public int getTo() {
return this.to;
}
public Node getNext() {
return this.next;
}
public int getLength() {
return this.to - this.from;
}
public String toString(final String word) {
return new StringBuilder()
.append("{")
.append("\"content\"")
.append(":")
.append("\"")
.append(word.substring(this.from, this.to))
.append("\"")
.append(",")
.append("\"next\"")
.append(":")
.append(this.next != null ? this.next.toString(word) : null)
.append("}")
.toString();
}
public boolean contains(final String word, final String suffix) {
if(this.next == null) {
return word.substring(this.from, this.to).equals(suffix);
}
return suffix.startsWith(word.substring(this.from,
this.to)) && this.next.contains(word, suffix.substring(this.to - this.from));
}
}
public class ActivePoint {
private final Node activeNode;
private final Character activeEdgeFirstCharacter;
private final int activeLength;
public ActivePoint(final Node activeNode,
final Character activeEdgeFirstCharacter,
final int activeLength) {
this.activeNode = activeNode;
this.activeEdgeFirstCharacter = activeEdgeFirstCharacter;
this.activeLength = activeLength;
}
private Edge getActiveEdge() {
return this.activeNode.getEdges().get(this.activeEdgeFirstCharacter);
}
public boolean pointsToActiveNode() {
return this.activeLength == 0;
}
public boolean activeNodeIs(final Node node) {
return this.activeNode == node;
}
public boolean activeNodeHasEdgeStartingWith(final char character) {
return this.activeNode.getEdges().containsKey(character);
}
public boolean activeNodeHasSlink() {
return this.activeNode.getSlink() != null;
}
public boolean pointsToOnActiveEdge(final String word, final char character) {
return word.charAt(this.getActiveEdge().getFrom() + this.activeLength) == character;
}
public boolean pointsToTheEndOfActiveEdge() {
return this.getActiveEdge().getLength() == this.activeLength;
}
public boolean pointsAfterTheEndOfActiveEdge() {
return this.getActiveEdge().getLength() < this.activeLength;
}
public ActivePoint moveToEdgeStartingWithAndByOne(final char character) {
return new ActivePoint(this.activeNode, character, 1);
}
public ActivePoint moveToNextNodeOfActiveEdge() {
return new ActivePoint(this.getActiveEdge().getNext(), null, 0);
}
public ActivePoint moveToSlink() {
return new ActivePoint(this.activeNode.getSlink(),
this.activeEdgeFirstCharacter,
this.activeLength);
}
public ActivePoint moveTo(final Node node) {
return new ActivePoint(node, this.activeEdgeFirstCharacter, this.activeLength);
}
public ActivePoint moveByOneCharacter() {
return new ActivePoint(this.activeNode,
this.activeEdgeFirstCharacter,
this.activeLength + 1);
}
public ActivePoint moveToEdgeStartingWithAndByActiveLengthMinusOne(final Node node,
final char character) {
return new ActivePoint(node, character, this.activeLength - 1);
}
public ActivePoint moveToNextNodeOfActiveEdge(final String word, final int index) {
return new ActivePoint(this.getActiveEdge().getNext(),
word.charAt(index - this.activeLength + this.getActiveEdge().getLength()),
this.activeLength - this.getActiveEdge().getLength());
}
public void addEdgeToActiveNode(final char character, final Edge edge) {
this.activeNode.getEdges().put(character, edge);
}
public void splitActiveEdge(final String word,
final Node nodeToAdd,
final int index,
final char character) {
final Edge activeEdgeToSplit = this.getActiveEdge();
final Edge splittedEdge = new Edge(activeEdgeToSplit.getFrom(),
activeEdgeToSplit.getFrom() + this.activeLength,
nodeToAdd);
nodeToAdd.getEdges().put(word.charAt(activeEdgeToSplit.getFrom() + this.activeLength),
new Edge(activeEdgeToSplit.getFrom() + this.activeLength,
activeEdgeToSplit.getTo(),
activeEdgeToSplit.getNext()));
nodeToAdd.getEdges().put(character, new Edge(index, word.length(), null));
this.activeNode.getEdges().put(this.activeEdgeFirstCharacter, splittedEdge);
}
public Node setSlinkTo(final Node previouslyAddedNodeOrAddedEdgeNode,
final Node node) {
if(previouslyAddedNodeOrAddedEdgeNode != null) {
previouslyAddedNodeOrAddedEdgeNode.setSlink(node);
}
return node;
}
public Node setSlinkToActiveNode(final Node previouslyAddedNodeOrAddedEdgeNode) {
return setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, this.activeNode);
}
}
private static int idGenerator;
private final String word;
private final Node root;
private ActivePoint activePoint;
private int remainder;
public ST(final String word) {
this.word = word;
this.root = new Node(idGenerator++);
this.activePoint = new ActivePoint(this.root, null, 0);
this.remainder = 0;
build();
}
private void build() {
for(int i = 0; i < this.word.length(); i++) {
add(i, this.word.charAt(i));
}
}
private void add(final int index, final char character) {
this.remainder++;
boolean characterFoundInTheTree = false;
Node previouslyAddedNodeOrAddedEdgeNode = null;
while(!characterFoundInTheTree && this.remainder > 0) {
if(this.activePoint.pointsToActiveNode()) {
if(this.activePoint.activeNodeHasEdgeStartingWith(character)) {
activeNodeHasEdgeStartingWithCharacter(character, previouslyAddedNodeOrAddedEdgeNode);
characterFoundInTheTree = true;
}
else {
if(this.activePoint.activeNodeIs(this.root)) {
rootNodeHasNotEdgeStartingWithCharacter(index, character);
}
else {
previouslyAddedNodeOrAddedEdgeNode = internalNodeHasNotEdgeStartingWithCharacter(index,
character, previouslyAddedNodeOrAddedEdgeNode);
}
}
}
else {
if(this.activePoint.pointsToOnActiveEdge(this.word, character)) {
activeEdgeHasCharacter();
characterFoundInTheTree = true;
}
else {
if(this.activePoint.activeNodeIs(this.root)) {
previouslyAddedNodeOrAddedEdgeNode = edgeFromRootNodeHasNotCharacter(index,
character,
previouslyAddedNodeOrAddedEdgeNode);
}
else {
previouslyAddedNodeOrAddedEdgeNode = edgeFromInternalNodeHasNotCharacter(index,
character,
previouslyAddedNodeOrAddedEdgeNode);
}
}
}
}
}
private void activeNodeHasEdgeStartingWithCharacter(final char character,
final Node previouslyAddedNodeOrAddedEdgeNode) {
this.activePoint.setSlinkToActiveNode(previouslyAddedNodeOrAddedEdgeNode);
this.activePoint = this.activePoint.moveToEdgeStartingWithAndByOne(character);
if(this.activePoint.pointsToTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
private void rootNodeHasNotEdgeStartingWithCharacter(final int index, final char character) {
this.activePoint.addEdgeToActiveNode(character, new Edge(index, this.word.length(), null));
this.activePoint = this.activePoint.moveTo(this.root);
this.remainder--;
assert this.remainder == 0;
}
private Node internalNodeHasNotEdgeStartingWithCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
this.activePoint.addEdgeToActiveNode(character, new Edge(index, this.word.length(), null));
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkToActiveNode(previouslyAddedNodeOrAddedEdgeNode);
if(this.activePoint.activeNodeHasSlink()) {
this.activePoint = this.activePoint.moveToSlink();
}
else {
this.activePoint = this.activePoint.moveTo(this.root);
}
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private void activeEdgeHasCharacter() {
this.activePoint = this.activePoint.moveByOneCharacter();
if(this.activePoint.pointsToTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
private Node edgeFromRootNodeHasNotCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
final Node newNode = new Node(idGenerator++);
this.activePoint.splitActiveEdge(this.word, newNode, index, character);
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, newNode);
this.activePoint = this.activePoint.moveToEdgeStartingWithAndByActiveLengthMinusOne(this.root,
this.word.charAt(index - this.remainder + 2));
this.activePoint = walkDown(index);
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private Node edgeFromInternalNodeHasNotCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
final Node newNode = new Node(idGenerator++);
this.activePoint.splitActiveEdge(this.word, newNode, index, character);
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, newNode);
if(this.activePoint.activeNodeHasSlink()) {
this.activePoint = this.activePoint.moveToSlink();
}
else {
this.activePoint = this.activePoint.moveTo(this.root);
}
this.activePoint = walkDown(index);
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private ActivePoint walkDown(final int index) {
while(!this.activePoint.pointsToActiveNode()
&& (this.activePoint.pointsToTheEndOfActiveEdge() || this.activePoint.pointsAfterTheEndOfActiveEdge())) {
if(this.activePoint.pointsAfterTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge(this.word, index);
}
else {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
return this.activePoint;
}
public String toString(final String word) {
return this.root.toString(word);
}
public boolean contains(final String suffix) {
return this.root.contains(this.word, suffix);
}
public static void main(final String[] args) {
final String[] words = {
"abcabcabc$",
"abc$",
"abcabxabcd$",
"abcabxabda$",
"abcabxad$",
"aabaaabb$",
"aababcabcd$",
"ababcabcd$",
"abccba$",
"mississipi$",
"abacabadabacabae$",
"abcabcd$",
"00132220$"
};
Arrays.stream(words).forEach(word -> {
System.out.println("Building suffix tree for word: " + word);
final ST suffixTree = new ST(word);
System.out.println("Suffix tree: " + suffixTree.toString(word));
for(int i = 0; i < word.length() - 1; i++) {
assert suffixTree.contains(word.substring(i)) : word.substring(i);
}
});
}
}