Modèles thématiques: validation croisée avec loglikelihood ou perplexité
je regroupe des documents en utilisant la modélisation thématique. Je dois trouver le nombre optimal de sujets. Donc, j'ai décidé de faire dix fois la validation croisée avec les sujets 10, 20, ...60.
j'ai divisé mon corpus en dix lots et mis de côté un lot pour un holdout set. J'ai effectué une analyse de l'allocation de dirichlet latent (LDA) en utilisant neuf lots (au total 180 documents) portant sur les sujets 10 à 60. Maintenant, je dois calculer la perplexité ou la probabilité logarithmique pour le jeu de Hold-Out.
j'ai trouvé ce code d'une des sessions de discussion du CV. Je ne comprends vraiment pas plusieurs lignes de codes ci-dessous. J'ai la matrice dtm en utilisant le jeu de holdout (20 documents). Mais je ne sais pas comment calculer la perplexité ou log-vraisemblance de ce jeu d'exclusion.
Questions:
-
est-ce que quelqu'un peut m'expliquer ce que seq(2, 100, by =1) signifie ici? Aussi, ce AssociatedPress [21:30] mean? Quelle est la fonction(k) est en train de faire ici?
best.model <- lapply(seq(2, 100, by=1), function(k){ LDA(AssociatedPress[21:30,], k) }) -
si je veux calculer la perplexité ou la probabilité logarithmique de l'ensemble de données appelé dtm, y a-t-il un meilleur code? Je sais qu'il y a des fonctions
perplexity()etlogLik()mais comme je suis nouveau, je ne peux pas trouver comment l'implémenter avec ma matrice de holdout, appelée dtm. -
Comment puis-je faire dix fois la validation croisée avec mon corpus, contenant 200 documents? Est-il code existant que je peux invoquer? J'ai trouvé
caretà cette fin, mais ne peut pas comprendre cela.
2 réponses
la réponse acceptée à cette question Est Bonne dans la mesure où elle va, mais elle ne traite pas réellement de la façon d'estimer la perplexité sur un ensemble de données de validation et de la façon d'utiliser la validation croisée.
à l'Aide de perplexité pour la simple validation
Perplexité est une mesure de la façon dont un modèle de probabilité correspond à un nouvel ensemble de données. Dans le paquet topicmodels R, Il est facile de s'adapter à la fonction perplexity , qui prend arguments un modèle de sujet précédemment adapté et un nouvel ensemble de données, et renvoie un nombre unique. Plus le mieux.
par exemple, fractionner les données AssociatedPress en un ensemble de formation (75% des lignes) et un ensemble de validation (25% des lignes):
# load up some R packages including a few we'll need later
library(topicmodels)
library(doParallel)
library(ggplot2)
library(scales)
data("AssociatedPress", package = "topicmodels")
burnin = 1000
iter = 1000
keep = 50
full_data <- AssociatedPress
n <- nrow(full_data)
#-----------validation--------
k <- 5
splitter <- sample(1:n, round(n * 0.75))
train_set <- full_data[splitter, ]
valid_set <- full_data[-splitter, ]
fitted <- LDA(train_set, k = k, method = "Gibbs",
control = list(burnin = burnin, iter = iter, keep = keep) )
perplexity(fitted, newdata = train_set) # about 2700
perplexity(fitted, newdata = valid_set) # about 4300
la perplexité est plus grande pour l'ensemble de validation que pour l'ensemble de formation, car les sujets ont été optimisés sur la base de l'ensemble de formation.
à l'Aide de perplexité et de validation croisée pour déterminer un bon nombre de sujets
L'extension de cette idée à la validation croisée est simple. Divisez les données en différents sous-ensembles (par exemple 5), et chaque sous-ensemble obtient un tour comme jeu de validation et quatre tours comme partie du jeu de formation. Cependant, il est vraiment computationally intensive, en particulier lors de l'essai du plus grand nombre de sujets.
vous pourriez utiliser caret pour faire ça, mais je le soupçonne il ne s'occupe pas encore de modélisation. En tout cas, c'est le genre de chose que je préfère faire moi-même pour être sûr de comprendre ce qui se passe.
le code ci-dessous, même avec un traitement parallèle sur 7 CPU logiques, a pris 3,5 heures pour fonctionner sur mon ordinateur portable:
#----------------5-fold cross-validation, different numbers of topics----------------
# set up a cluster for parallel processing
cluster <- makeCluster(detectCores(logical = TRUE) - 1) # leave one CPU spare...
registerDoParallel(cluster)
# load up the needed R package on all the parallel sessions
clusterEvalQ(cluster, {
library(topicmodels)
})
folds <- 5
splitfolds <- sample(1:folds, n, replace = TRUE)
candidate_k <- c(2, 3, 4, 5, 10, 20, 30, 40, 50, 75, 100, 200, 300) # candidates for how many topics
# export all the needed R objects to the parallel sessions
clusterExport(cluster, c("full_data", "burnin", "iter", "keep", "splitfolds", "folds", "candidate_k"))
# we parallelize by the different number of topics. A processor is allocated a value
# of k, and does the cross-validation serially. This is because it is assumed there
# are more candidate values of k than there are cross-validation folds, hence it
# will be more efficient to parallelise
system.time({
results <- foreach(j = 1:length(candidate_k), .combine = rbind) %dopar%{
k <- candidate_k[j]
results_1k <- matrix(0, nrow = folds, ncol = 2)
colnames(results_1k) <- c("k", "perplexity")
for(i in 1:folds){
train_set <- full_data[splitfolds != i , ]
valid_set <- full_data[splitfolds == i, ]
fitted <- LDA(train_set, k = k, method = "Gibbs",
control = list(burnin = burnin, iter = iter, keep = keep) )
results_1k[i,] <- c(k, perplexity(fitted, newdata = valid_set))
}
return(results_1k)
}
})
stopCluster(cluster)
results_df <- as.data.frame(results)
ggplot(results_df, aes(x = k, y = perplexity)) +
geom_point() +
geom_smooth(se = FALSE) +
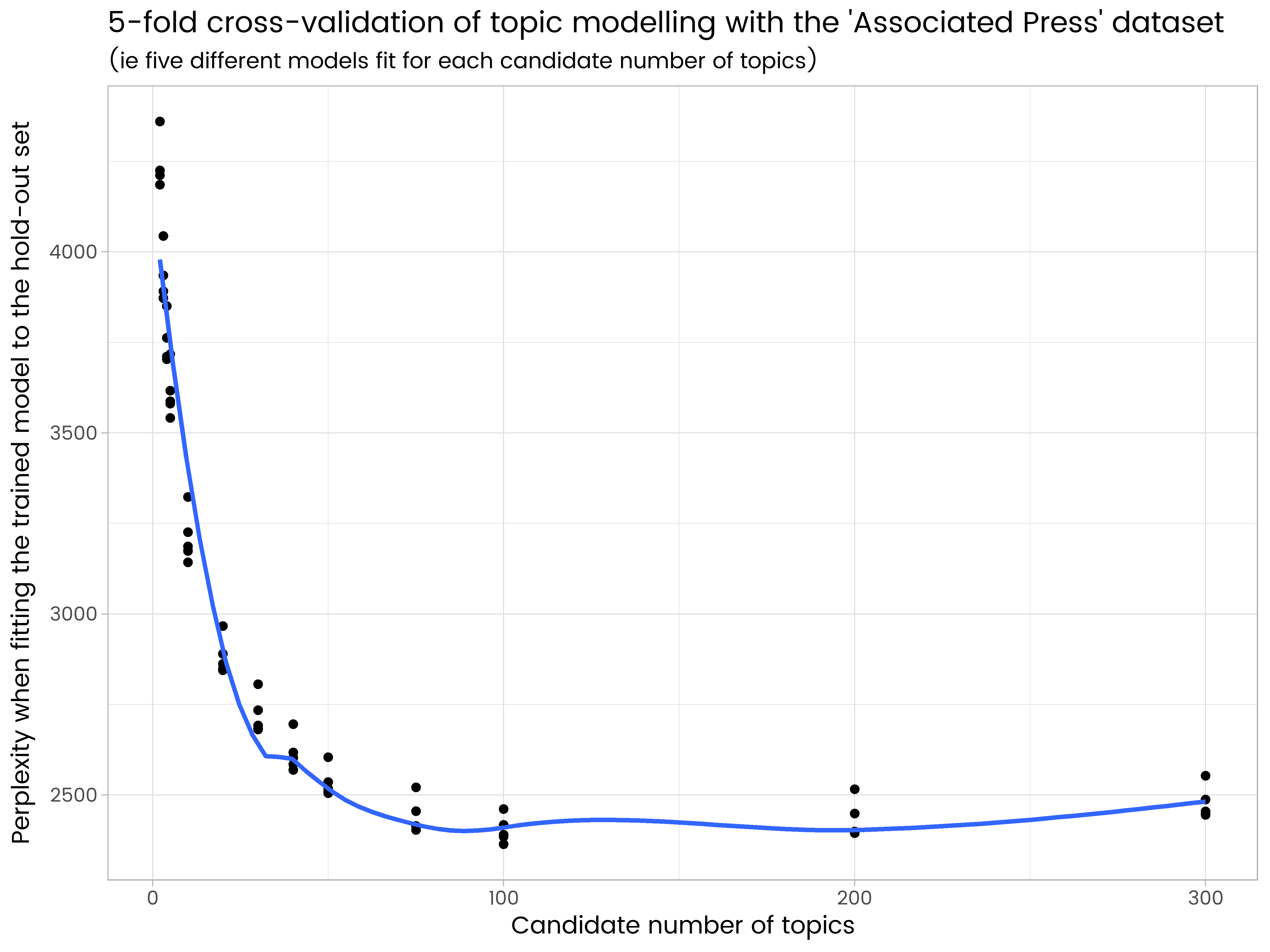
ggtitle("5-fold cross-validation of topic modelling with the 'Associated Press' dataset",
"(ie five different models fit for each candidate number of topics)") +
labs(x = "Candidate number of topics", y = "Perplexity when fitting the trained model to the hold-out set")
nous voyons dans les résultats que 200 sujets est trop nombreux et a certains trop ajustés, et 50 est trop peu. Sur le nombre de sujets essayés, 100 est le meilleur, avec la plus faible moyenne de perplexité sur les cinq différent de " hold-out jeux.
j'ai écrit la réponse sur CV que vous vous référez, voici un peu plus de détails:
-
seq(2, 100, by =1)crée simplement une séquence de nombres de 2 à 100 par uns, donc 2, 3, 4, 5,... 100. Ce sont les chiffres de sujets que je veux utiliser dans les modèles. Un modèle avec 2 sujets, un autre avec 3 sujets, un autre avec 4 sujets et ainsi de suite à 100 sujets. -
AssociatedPress[21:30]est simplement un sous-ensemble du système intégré données dans le paquettopicmodels. J'ai juste utilisé un sous-ensemble dans cet exemple, afin qu'il s'exécute plus rapidement.
en ce qui concerne la question générale du nombre optimal de sujets, je suis maintenant L'exemple de Martin Ponweiser sur la sélection de modèle Par moyen harmonique (4.3.3 dans sa thèse, qui est ici: http://epub.wu.ac.at/3558/1/main.pdf ). Voici comment je le fais en ce moment:
library(topicmodels)
#
# get some of the example data that's bundled with the package
#
data("AssociatedPress", package = "topicmodels")
harmonicMean <- function(logLikelihoods, precision=2000L) {
library("Rmpfr")
llMed <- median(logLikelihoods)
as.double(llMed - log(mean(exp(-mpfr(logLikelihoods,
prec = precision) + llMed))))
}
# The log-likelihood values are then determined by first fitting the model using for example
k = 20
burnin = 1000
iter = 1000
keep = 50
fitted <- LDA(AssociatedPress[21:30,], k = k, method = "Gibbs",control = list(burnin = burnin, iter = iter, keep = keep) )
# where keep indicates that every keep iteration the log-likelihood is evaluated and stored. This returns all log-likelihood values including burnin, i.e., these need to be omitted before calculating the harmonic mean:
logLiks <- fitted@logLiks[-c(1:(burnin/keep))]
# assuming that burnin is a multiple of keep and
harmonicMean(logLiks)
donc pour faire ceci au-dessus d'un séquence de modèles de sujets avec différents nombres de sujets...
# generate numerous topic models with different numbers of topics
sequ <- seq(2, 50, 1) # in this case a sequence of numbers from 1 to 50, by ones.
fitted_many <- lapply(sequ, function(k) LDA(AssociatedPress[21:30,], k = k, method = "Gibbs",control = list(burnin = burnin, iter = iter, keep = keep) ))
# extract logliks from each topic
logLiks_many <- lapply(fitted_many, function(L) L@logLiks[-c(1:(burnin/keep))])
# compute harmonic means
hm_many <- sapply(logLiks_many, function(h) harmonicMean(h))
# inspect
plot(sequ, hm_many, type = "l")
# compute optimum number of topics
sequ[which.max(hm_many)]
## 6
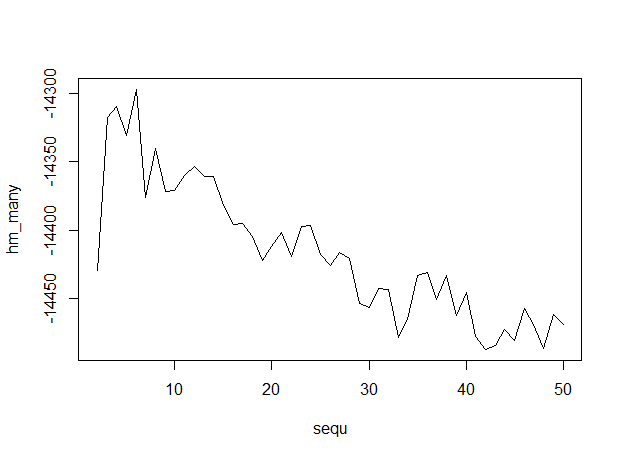 Voici le résultat, avec un nombre de sujets le long de l'axe des x, indiquant que 6 sujets est optimal.
Voici le résultat, avec un nombre de sujets le long de l'axe des x, indiquant que 6 sujets est optimal.
la validation croisée des modèles de sujets est assez bien documentée dans les docs qui accompagnent le paquet, voir par exemple: http://cran.r-project.org/web/packages/topicmodels/vignettes/topicmodels.pdf Give that a try et puis revenir avec une question plus spécifique sur le codage CV avec des modèles de sujet.