Regroupement du texte avec les distances Levenshtein
j'ai un ensemble (2k - 4k) de petites chaînes (3-6 caractères) et je veux les regrouper. Depuis que j'utilise strings, les réponses précédentes sur Comment fonctionne le clustering (en particulier le clustering String)? , m'a informé que distance Levenshtein est bon à utiliser comme une fonction de distance pour les cordes. En outre, comme je ne sais pas à l'avance le nombre de grappes, regroupement hiérarchique est la voie à suivre et non k-signifie.
bien que j'obtienne le problème dans sa forme abstraite, Je ne sais pas quelle est la façon facile de le faire réellement. Par exemple, est MATLAB ou R un meilleur choix pour la mise en œuvre réelle de regroupement hiérarchique avec la fonction personnalisée (distance Levenshtein). Pour les deux logiciels, on peut facilement trouver une implémentation de distance Levenshtein. La partie de regroupement semble plus difficile. Par exemple texte de regroupement dans MATLAB calcule le tableau de distance pour tous strings, mais je ne peux pas comprendre comment utiliser le tableau distance pour obtenir le clustering. Pouvez-vous, gourous, me montrer comment mettre en œuvre le clustering hiérarchique dans MATLAB ou R avec une fonction personnalisée?
4 réponses
cela peut être un peu simpliste, mais voici un exemple de code qui utilise le regroupement hiérarchique basé sur la distance Levenshtein en R.
set.seed(1)
rstr <- function(n,k){ # vector of n random char(k) strings
sapply(1:n,function(i){do.call(paste0,as.list(sample(letters,k,replace=T)))})
}
str<- c(paste0("aa",rstr(10,3)),paste0("bb",rstr(10,3)),paste0("cc",rstr(10,3)))
# Levenshtein Distance
d <- adist(str)
rownames(d) <- str
hc <- hclust(as.dist(d))
plot(hc)
rect.hclust(hc,k=3)
df <- data.frame(str,cutree(hc,k=3))
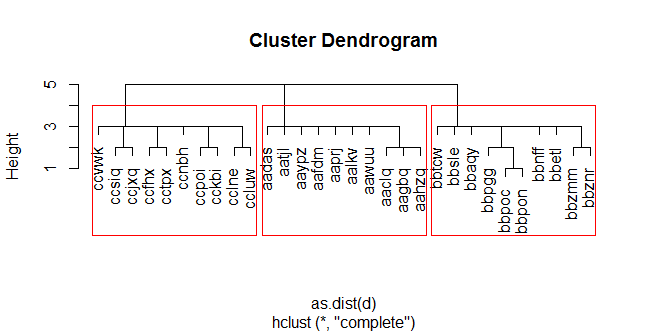
dans cet exemple, nous créons un ensemble de 30 chaînes de caractères aléatoires(5) artificiellement en 3 groupes (en commençant par" aa"," bb", et"cc"). Nous calculons la matrice de distance de Levenshtein en utilisant adist(...) , et nous exécutons le clustering heirarchal en utilisant hclust(...) . Nous avons ensuite coupé l' dendrogramme en trois clusters avec cutree(...) et ajouter les cluster id aux chaînes originales.
ELKI inclut la distance Levenshtein, et offre un large choix d'algorithmes avancés de clustering, par exemple optique clustering.
Text prise en charge des clusters a été contribué par Felix Stahlberg, dans le cadre de son travail sur:
Stahlberg, F., Schlippe, T., Vogel, S., & Schultz, T.
segmentation des mots par le biais de cross-lingual mot-à-phonème alignement.
la Langue Parlée Atelier de la Technologie (SLT), 2012 IEEE. IEEE, 2012.
nous aimerions bien sûr recevoir des contributions supplémentaires.
alors que la réponse dépend dans une certaine mesure du signifiant des cordes, en général votre problème est résolu par la famille de techniques d'analyse de séquence. Plus précisément, L'analyse de correspondance optimale (OMA).
le Plus souvent l'OMA est réalisée en trois étapes. Tout d'abord, vous définissez vos séquences. De votre description je peux supposer que chaque lettre est un "État" séparé, le bloc de construction dans une séquence. Deuxièmement, vous devrez utiliser l'une des plusieurs algorithmes pour calculer les distances entre toutes les séquences de votre ensemble de données, ce qui permet d'obtenir la matrice des distances. Enfin, vous introduirez cette matrice de distance dans un algorithme de clustering, tel que le clustering hiérarchique ou le partitionnement autour de Medoids (PAM), qui semble gagner en popularité grâce aux informations supplémentaires sur la qualité des clusters. Ce dernier vous guide dans le choix du nombre de grappes, l'une des étapes subjectives de l'analyse séquentielle.
dans" 15191092020 "le paquet le plus commode avec un grand nombre de fonctions est TraMineR , le site web peut être trouvé ici . Son guide utilisateur est très accessible, et les développeurs sont plus ou moins actifs sur ainsi.
Vous êtes susceptibles de trouver que le regroupement n'est pas la partie la plus difficile, sauf pour la décision sur le nombre de clusters. Le guide TraMineR montre que la syntaxe est très compliquée, et les résultats sont faciles à interpréter basée sur la séquence visuelle des graphiques. Voici un exemple tiré du guide de l'utilisateur:
clusterward1 <- agnes(dist.om1, diss = TRUE, method = "ward")
dist.om1 est la matrice de distance obtenue par OMA, l'appartenance à un cluster est contenue dans l'objet clusterward1 , que vous pouvez faire ce que vous voulez: tracer, recoder comme variables etc. L'option diss=TRUE indique que l'objet de données est la matrice de dissimilarité (ou de distance). Facile, hein? Le plus difficile le choix (pas syntaxique, mais méthodologique) est de choisir l'algorithme de la bonne distance, adapté à votre application particulière. Une fois que vous avez cela, être en mesure de justifier le choix, le reste est assez facile. Bonne chance!
si vous souhaitez une explication claire de la façon d'utiliser la segmentation de partitions (qui sera sûrement plus rapide) pour résoudre votre problème, consultez cet article: méthodes efficaces de vérification orthographique utilisant des algorithmes de segmentation. https://www.researchgate.net/publication/255965260_Effective_Spell_Checking_Methods_Using_Clustering_Algorithms?ev=prf_pub
les auteurs expliquent comment regrouper un dictionnaire à l'aide d'une version modifiée (semblable à PAM) de Ik-Means.
bonne chance!