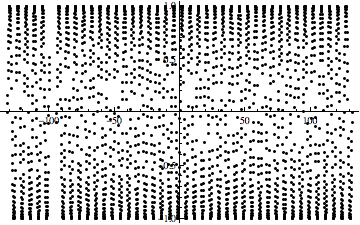
Strange Sin [x] graphe dans Mathematica
j'ai tracé au hasard une fonction Sin[x] dans Mathematica 7 Et voici ce qu'elle montre:
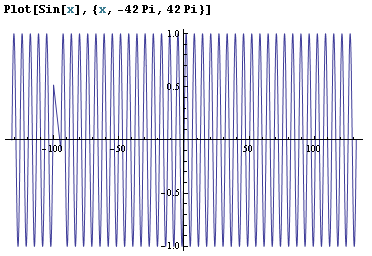
noter le défaut visible à environ x = -100.
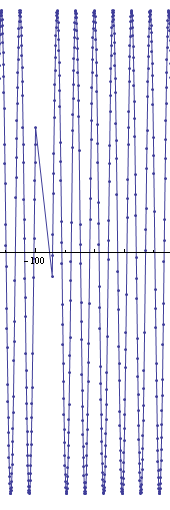
N'importe qui sait pourquoi cela arrive et pourquoi seulement à x = -100?
Note: la même chose se produit dans Wolfram Alpha, soit dit en passant.
1 réponses
réponse courte: la précision de pointage par défaut n'est pas suffisante pour cette fonction, donc augmentez-la comme suit
Plot[Sin[x], {x, -42 Pi, 42 Pi}, PlotPoints -> 100]
réponse: Plot fonctionne en évaluant la fonction à un ensemble fini de points, et la connexion de ces points par des lignes droites. Vous pouvez voir les points utilisés par Plot en utilisant la commande suivante
Plot[Sin[x], {x, -42 Pi, 42 Pi}, Mesh -> All, PlotStyle -> None,
MeshStyle -> Black]
Vous pouvez voir que pour votre fonction, les points où la fonction a été évaluée comme ayant "manqué le pic" et a introduit une erreur d'approximation importante. L'algorithme utilisé pour choisir l'emplacement des points est très simple et cette situation peut se produire lorsque deux pics sont espacés plus étroitement que PlotRange/PlotPoints.
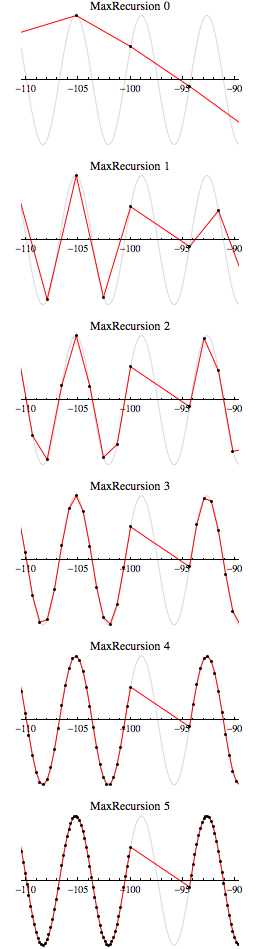
Plot commence avec 50 points également espacés, puis y insère des points supplémentaires jusqu'à MaxRecursion étapes. Vous pouvez voir comment ce" trou " apparaît si vous tracez la région pour différents paramètres de MaxRecursion.
plot1 = Plot[Sin[x], {x, -42 Pi, 42 Pi}, PlotPoints -> 100,
PlotStyle -> LightGray];
Table[plot2 =
Plot[Sin[x], {x, -42 Pi, 42 Pi}, Mesh -> All, MeshStyle -> Thick,
PlotStyle -> Red, MaxRecursion -> k];
Show[plot1, plot2, PlotRange -> {{-110, -90}, {-1, 1}},
PlotLabel -> ("MaxRecursion " <> ToString[k])], {k, 0,
5}] // GraphicsColumn
selon le Livre de Mathematica de Stan Wagon,Plot décide d'ajouter ou non un point supplémentaire à mi-chemin entre deux points consécutifs si l'angle entre deux nouveaux segments de ligne est supérieur à 5 degrés. Dans le cas présent, plot n'a pas eu de chance avec la position initiale du point et la subdivision ne répond pas à ce critère. Vous pouvez voir que l'insertion d'une évaluation unique point dans le centre du trou va produire une parcelle de terrain à l'apparence presque identique.
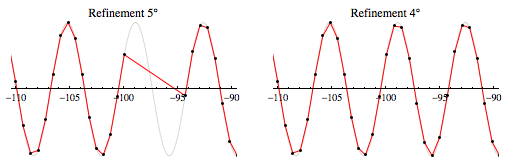
la façon d'augmenter l'angle utilisé pour décider quand subdiviser en utilisant Refinement option (je l'ai eu à partir du livre, mais il ne semble pas être documentée dans le produit)
plot1 = Plot[Sin[x], {x, -42 Pi, 42 Pi}, PlotPoints -> 100,
PlotStyle -> LightGray];
Show[plot1,
Plot[Sin[x], {x, -42 Pi, 42 Pi}, Mesh -> All, MeshStyle -> Thick,
PlotStyle -> Red, MaxRecursion -> 3,
Method -> {Refinement -> {ControlValue -> 4 \[Degree]}}],
PlotRange -> {{-110, -90}, {-1, 1}}]
ici vous pouvez voir que l'augmenter de 1 degré à partir de la valeur par défaut 5 corrige le trou.