Étapes pour créer un NFA à partir d'une expression régulière

Version courte pour l'approche générale.
Il y a un algo là-bas appelé L'algorithme de construction Thompson-McNaughton-Yamada ou parfois juste " Thompson Construction."On construit des NFA intermédiaires, remplissant les pièces en cours de route, tout en respectant la priorité de l'opérateur: premières parenthèses, puis étoile de Kleene (par exemple, a*), puis concaténation (par exemple, ab), suivie d'une alternance (par exemple, a|b).

Voici une procédure pas à pas en profondeur pour la construction (b / a)*b(a|b) ' s NFA

Construire le niveau supérieur

1. Gérer les parenthèses. Note: dans l'implémentation réelle, il peut être logique de gérer les parenthèses via un appel récursif sur leur contenu. Par souci de clarté, je vais reporter l'évaluation de tout ce qui se trouve à l'intérieur de parens.

2. Étoiles Kleene: un seul * là, donc nous construisons une machine à étoiles Kleene appelée P (qui contiendra plus tard b|a). Intermédiaire résultat:
   

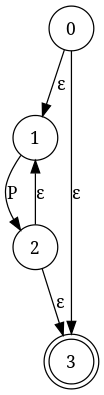
3. Concaténation: attachez P à b et attachez b à une machine d'espace réservé appelée Q (qui contiendra (a / b). Résultat intermédiaire:
   

4. Il n'y a pas d'alternance en dehors des parenthèses, donc nous l'ignorons.

Maintenant, nous sommes assis sur une machine P*bQ. (Notez que nos espaces réservés P et Q ne sont que des machines de concaténation.) On remplace le bord P par le NFA pour b / a, et on remplace le bord Q par le NFA pour A / b Via récursif l'application de la procédure ci-dessus.

Bâtiment P

1. Skip. Pas de parens.

2. Skip. Pas d'étoiles Kleene.

3. Skip. Pas de contatenation.

4. Construire l'alternance de la machine pour b|a. Résultat intermédiaire:
   

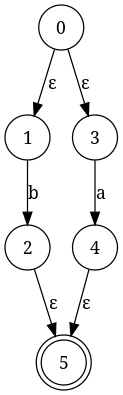
L'Intégration De P

Ensuite, nous revenons à cette machine P*bQ et nous arrachons le bord P. Nous avons la source du bord P servir de départ l'état de destination pour la machine P, et la destination du bord p servent d'état de destination pour la machine P. Nous faisons également rejeter cet état (enlever sa propriété d'être un État d'acceptation). Le résultat ressemble à ceci: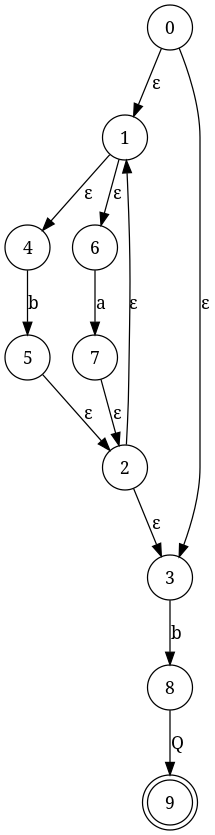

Bâtiment Q

1. Skip. Pas de parens.

2. Skip. Pas d'étoiles Kleene.

3. Skip. Pas de contatenation.

4. Construire la machine d'alternance pour a / B. incidemment, l'alternance est commutative, donc a / b est logiquement équivalent à b / A. (Lire: sauter ce diagramme de note de bas de page mineur par paresse.)

L'Intégration De Q

Nous faisons ce que nous avons fait avec P ci-dessus, sauf en remplaçant le bord Q par la machine intermedtae b|a que nous avons construite. C'est le résultat: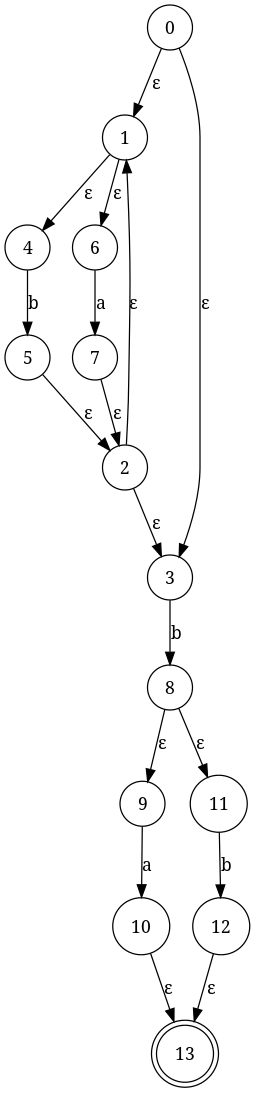

Tada! Euh, je veux dire, QED.

Vous voulez en savoir plus?

Toutes les images ci-dessus ont été générées à l'aide de un outil en ligne pour conversion automatique d'expressions régulières en automates finis non déterministes . Vous pouvez trouver son code source pour L'algorithme de construction Thompson-McNaughton-Yamada en ligne.

L'algorithme est également abordé dans les compilateurs Aho: Principles, Techniques, and Tools , bien que son explication soit clairsemée sur les détails de l'implémentation. Vous pouvez également apprendre de une implémentation de la construction Thompson en C par L'excellent Russ Cox, qui décrit quelques détails dans un article populaire sur expression régulière correspondant .